力の平行四辺形

テンプレート:Anchors図1: 力を表す（平行でない）ベクトルの組による平行四辺形の作図。対角線が合力を表す。

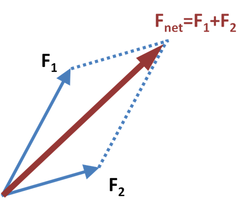
力の平行四辺形（ちからのへいこうしへんけい、テンプレート:Lang-en-short）は、物体に2つの力の加法によって得られる平行四辺形である。力の平行四辺形は、2つの力の合力を図示するためにしばしば用いられる。

2つより多くの力のなす図形はもはや平行四辺形ではなくなるが、それらの合力がなす図として同様に平行四辺形を作図できる。例えば、図1では、テンプレート:Math の始点が テンプレート:Math の終点と一致するように テンプレート:Math を移動させるのと、テンプレート:Math の始点と テンプレート:Math の終点を結ぶベクトルを正味の力とするのとでは同じ結果になる。3つのベクトル テンプレート:Math2 の合力の場合も同様に、テンプレート:Math と テンプレート:Math のなす平行四辺形として作図できる（結果は和の順序に依存しない）。

ニュートンの証明

図2: 速度の平行四辺形

準備: 速度の平行四辺形

与えられた時間（例えば1秒）で粒子がAからBへの線（図2）に沿って一定の速度で移動し、同時に線ABがABの位置からDCの位置に一様に移動し、終始元の方向と平行なままであるとする。両方の運動を考慮すると、粒子は線ACをたどる。与えられた時間内の変位は速度の尺度なので、ABの長さはABに沿った粒子の速度の尺度であり、ADの長さはADに沿った線の速度の尺度であり、ACの長さはACに沿った粒子の速度の尺度である。粒子の運動はACに沿って単一の速度で移動した場合と同じである。

力の平行四辺形のニュートンの証明

図1の原点（ベクトルの「尾」）にある粒子に2つの力が作用したとする。ベクトルF₁とF₂の長さは2つの力がある時間作用することにより粒子に生じる速度を表し、それぞれの方向はそれが作用する方向を表している。それぞれの力は独立に作用し、他の力が作用するかしないかにかかわらず特定の速度を作り出す。与えられた時間の終わりでは、粒子は両方の速度を持っている。上記の証明により、これは1つの速度F_netと等価である。ニュートンの第2法則により、このベクトルはその速度を生み出す力の尺度でもあり、したがって、2つの力は1つの力と等価である。

平行四辺形を用いてなめらかな斜面上の粒子に作用する力を加える。予想通り、結果として生じる力（頭が2つの矢印）が斜面の下向きに作用し、粒子がその方向に加速することが分かる。

垂直なベクトルに対するベルヌーイの証明

力をユークリッドベクトルもしくは${ℝ}^2$の要素としてモデル化する。最初の仮定は2つの力の合力が実際には別の力であるというものである。すなわち、任意の2つの力$𝐅,𝐆\in {ℝ}^2$に対して、$𝐅\oplus 𝐆\in {ℝ}^2$が存在する。 最後の仮定は2つの力の合力が回転しても変化しないことである。$R:{ℝ}^2\to {ℝ}^2$を任意の回転（$\det R=1$である${ℝ}^2$の通常のベクトル空間構造の任意の直交写像）とすると、任意の力$𝐅,𝐆\in {ℝ}^2$に対し$R$は

$$R(𝐅\oplus 𝐆)=R\left(𝐅\right)\oplus R\left(𝐆\right)$$

を満たす。2つの力${𝐅}_1$と${𝐅}_2$は垂直で、${𝐅}_1$の長さを$a$、${𝐅}_2$の長さを$b$、および${𝐅}_1\oplus {𝐅}_2$の長さを$x$と仮定する。 ${𝐆}_1:=\frac{a^2}{x^2}({𝐅}_1\oplus {𝐅}_2)$および${𝐆}_2:=\frac{a}{x}R({𝐅}_2)$として、$R$を${𝐅}_1$と${𝐅}_1\oplus {𝐅}_2$の間の回転とすると${𝐆}_{\mathrm{𝟏}}=\frac{a}{x}R\left({𝐅}_1\right)$である。回転が不変の下では

$${𝐅}_1=\frac{x}{a}{R}^{-1}\left({𝐆}_1\right)=\frac{a}{x}{R}^{-1}({𝐅}_1\oplus {𝐅}_2)=\frac{a}{x}{R}^{-1}\left({𝐅}_1\right)\oplus \frac{a}{x}{R}^{-1}\left({𝐅}_2\right)={𝐆}_1\oplus {𝐆}_2$$

を得る。同様に、さらに2つの力${𝐇}_1:=-{𝐆}_2,{𝐇}_2:=\frac{b^2}{x^2}({𝐅}_1\oplus {𝐅}_2)$を考える。$T$を${𝐅}_1$から${𝐇}_1$への回転とすると${𝐇}_1=\frac{b}{x}T\left({𝐅}_1\right)$であり、これにより${𝐇}_2=\frac{b}{x}T\left({𝐅}_2\right)$となる。

$${𝐅}_2=\frac{x}{b}{T}^{-1}\left({𝐇}_2\right)=\frac{b}{x}{T}^{-1}({𝐅}_1\oplus {𝐅}_2)=\frac{b}{x}{T}^{-1}\left({𝐅}_1\right)\oplus \frac{b}{x}{T}^{-1}\left({𝐅}_2\right)={𝐇}_1\oplus {𝐇}_{\mathrm{𝟐}}$$

これら2つの方程式より

$${𝐅}_1\oplus {𝐅}_2=({𝐆}_1\oplus {𝐆}_2)\oplus ({𝐇}_1\oplus {𝐇}_{\mathrm{𝟐}})=({𝐆}_1\oplus {𝐆}_2)\oplus (-{𝐆}_2\oplus {𝐇}_2)={𝐆}_1\oplus {𝐇}_2$$

を得る。${𝐆}_1$と${𝐇}_2$はどちらも${𝐅}_1\oplus {𝐅}_2$に沿っているため、長さ$x$は$|{𝐅}_1\oplus {𝐅}_2|=|{𝐆}_1\oplus {𝐇}_2|=\frac{a^2}{x}+\frac{b^2}{x}$に等しく、

$$x=\sqrt{a^2+b^2}$$

である。このことは${𝐅}_1\oplus {𝐅}_2=a{𝐞}_1\oplus b{𝐞}_2$が長さ$\sqrt{a^2+b^2}$を持ち、これは$a{𝐞}_1+b{𝐞}_2$の長さであることを示している。したがって、${𝐅}_1$と${𝐅}_2$が垂直である場合、${𝐅}_1\oplus {𝐅}_2={𝐅}_1+{𝐅}_2$である。ここで、2つの補助の力を組み合わせるとき、$\oplus$の結合性を用いた。以下の証明にもこの追加の仮定を使用する 。

力の平行四辺形の代数的証明

力をユークリッドベクトルもしくは${ℝ}^2$の要素としてモデル化する。最初の仮定は2つの力の合力が実際には別の力であるというものである。そのため、2つの力$𝐅,𝐆\in {ℝ}^2$には、別の力$𝐅\oplus 𝐆\in {ℝ}^2$が存在する。可換性を仮定する。これらは同時に加えられる力なので、順序は重要ではなく、$𝐅\oplus 𝐆=𝐆\oplus 𝐅$である。

写像 $$(a,b)=a{𝐞}_1+b{𝐞}_2\mapsto a{𝐞}_1\oplus b{𝐞}_2$$ を考える。 $\oplus$が結合的であるならば、この写像は線形である。${𝐞}_1$を${𝐞}_1$に、${𝐞}_2$を${𝐞}_2$に写すため、恒等写像である必要もある。よって$\oplus$は通常のベクトル加算演算子と同等でなければならない。

論争

力の平行四辺形の数学的証明は、数学的に妥当であると一般に認められていない。さまざまな証明が開発され（主にDuchaylaとポアソンのもの）、これらも反論を引き起こした。力の平行四辺形が真実であるかどうかは疑問視されなかったが、なぜ真実であったのであろうか。今日、力の平行四辺形は経験的事実として受け入れられており、ニュートンの第1原理に還元することはできない。

関連項目

• Newton's Mathematical Principles of Natural Philosophy, Axioms or Laws of Motion, Corollary I, at Wikisource
• 空間ベクトル
• 合力