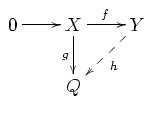入射加群

数学において、入射加群（にゅうしゃかぐん、テンプレート:Lang-en-short）、あるいは移入加群（いにゅうかぐん）とは、関手テンプレート:Math が完全となるような加群テンプレート:Mvar のことである。ホモロジー代数における基本的な概念のひとつ。

動機

0 \to N \to M \to K \to 0

に対して

0 \to Hom (K, Q) \to Hom (M, Q) \to Hom (N, Q)

は完全である。この関手テンプレート:Math が完全となる、つまり

0 \to Hom (K, Q) \to Hom (M, Q) \to Hom (N, Q) \to 0

が完全となる加群テンプレート:Mvar のことを移入加群と呼ぶ。

テンプレート:Mvar を単位元をもつ環とし、以下では加群はすべて左テンプレート:Mvar 加群、射はすべて左テンプレート:Mvar 加群の準同型を指すことにする。加群テンプレート:Mvar が移入加群であることは次のいずれの条件とも同値である。

環 R が自身の上の左加群として移入的であるとき、左自己移入環と呼ぶ。右自己移入環も同様。

左 R-加群 Q が移入加群であるための必要十分条件は、R の任意の左イデアル L と任意の準同型 L→Q に対して、その拡張 R→Q が存在することである。

加群テンプレート:Mvar に対し、各 $Q_{i}$ が移入加群であるような次の完全列

0 \to M \to Q_{0} \to Q_{1} \to \dots \to Q_{n} \to Q_{n + 1} \to \dots

をテンプレート:Mvar の移入分解という。任意の加群は移入分解をもつ。すべてのテンプレート:Math に対しテンプレート:Math であるような移入分解を長さテンプレート:Mvar の移入分解という。そのようなテンプレート:Mvar が存在する場合その最小値をテンプレート:Mvar の移入次元といい、存在しない場合は移入次元はテンプレート:Math という。ただし、テンプレート:Math の移入次元はテンプレート:Math とする。移入次元はテンプレート:Math と書かれる。テンプレート:Mvar-加群テンプレート:Mvar と整数テンプレート:Math に対して以下は同値。