屈折

光の屈折により、水面を境にしてペンが折れ曲がっているように見える。

プラスチックのブロックを通過する光束

屈折（くっせつ、テンプレート:Lang-en-short）とは、界面において、波（波動）が進行方向を変えることである。異なる媒質を通るときに、波の周波数が変わらずに進む速度が変わるため進行方向が変わるテンプレート:疑問点範囲。

光の屈折がもっとも身近な例であるが、例えば音波や水の波動も屈折する。波が進行方向を変える度合いとしてはホイヘンスの原理を使ったスネルの法則が成り立つ。部分的に反射する振る舞いはフレネルの式で表される。なぜ光が屈折するかについては、量子力学的にファインマンの経路積分によって説明される。

概要

水中の棒が上に曲がって見える図

例えば、光線がガラスを通ると、屈折して曲がっているように見えるが、これはガラスが空気と異なる屈折率を持っているためである。ガラスの表面に対して垂直に光が入射した場合、光の進行方向は変わらず、速度だけが変化するが、厳密にはこの場合も屈折という。

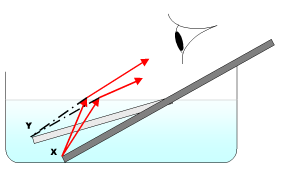
左の図のように、水中に差し込んだ棒が上方に曲がって見える現象は光の屈折で説明できる。空気の屈折率は約1.0003、水の屈折率は約1.3330と異なるため、水から反射した光は屈折して目に届く。つまり図の棒上のxに由来する光が水面で屈折を起こすため、Xの見かけ上の位置はYになる。これが水中の棒が実際より上方にあるように見せる。

屈折率が大きい媒質から小さい媒質に光が入るときに、入射光が境界面を屈折せず、すべて反射することを全反射という。この原理は光ファイバー等に使われる。等方的な媒質から異方的な媒質へ波が進む場合は、複屈折を起こす。

スネルの法則

スネルの法則の例

テンプレート:Main スネルの法則は二つの媒質中を進行する波の伝播速度と、入射角・屈折角の関係を表した法則。媒質Aにおける波の速度を$v_{\mathrm{A}}$、媒質Bにおける波の速度を$v_{\mathrm{B}}$、媒質Aから媒質Bへの入射角（またはBからAへの屈折角）を${\theta }_{\mathrm{A}}$、媒質Bから媒質Aへの入射角（またはAからBへの屈折角）を${\theta }_{\mathrm{B}}$とすると、以下の関係が成立する。

$\frac{\sin {\theta }_{\mathrm{A}}}{\sin {\theta }_{\mathrm{B}}}=\frac{v_{\mathrm{A}}}{v_{\mathrm{B}}}.$

ここで、$\frac{v_{\mathrm{A}}}{v_{\mathrm{B}}}$の値を媒質Aに対する媒質Bの相対屈折率と定義し、これを$n_{\mathrm{A}\mathrm{B}}$（または$n_{\mathrm{A}\mathrm{\to }\mathrm{B}}$）で表す。以上のことをまとめると

$\frac{\sin {\theta }_{\mathrm{A}}}{\sin {\theta }_{\mathrm{B}}}=\frac{v_{\mathrm{A}}}{v_{\mathrm{B}}}=n_{\mathrm{A}\mathrm{B}}.$

となる（図を参照）。

フレネルの式

テンプレート:Mainフレネルの式は、界面における光のふるまい（反射・屈折）を記述する式である。屈折率が$n$の媒質から$n^{\prime }$の媒質へ界面に垂直に光線が入射すると、入射光の強度を$I_0$とした場合の反射光の強度$I$は以下のように表される。

$I=I_0{\left(\frac{n-n^{\prime }}{n+n^{\prime }}\right)}^2.$

入射面の内側に偏光している光が、透明な媒質の表面で反射された場合の入射角を$i$、屈折角を$r$とすると、反射光の強度は以下のように表される。

$I=\left(\frac{I_0{\sin }^2(i-r)}{I_0{\sin }^2(i+r)}\right).$

入射面に垂直な方向に偏光している光の場合には以下のようになる。

$I=\left(\frac{I_0{\tan }^2(i-r)}{I_0{\tan }^2(i+r)}\right).$

自然現象

複屈折を示す方解石

虹、蜃気楼、幻日、逃げ水のほか、日没や日の出の時刻が天文学上の計算からずれるという形で現れる。音波の例としては、特定の天候に限って遠方の鉄道などの音がはっきり聞こえるというものがある。これは上空に逆転層が生じ、低温の空気では音速が下がるため、いったん上空に向かって進んだ音波が屈折し、再び地上に戻ってくると説明される。

応用機器

レンズ

プリズム

レンズ

凸レンズでは通した光を屈折させて一点に集中させ、凹レンズでは光を屈折させて並行に進ませることによって、観測している者に実像より拡大や縮小した像を見せる。レンズはカメラ、顕微鏡、望遠鏡、眼鏡などに使われる。

プリズム

媒質は光の波長によって異なるため、プリズムを出る光は波長の違いにより色ごとに分散する。この光の分散が虹のようなスペクトルを作り出す。

糖度計

試料液（測定対象となる液体）に、糖と水以外が入っていないことを前提に、水に含まれる糖の含有量によって光の屈折率が異なる性質を利用し、その試料の糖度を計る。

関連項目

• 屈折率
• 音速、光速度 (媒質中の波の速度)
• 回折
• 円偏光二色性
• メタマテリアル - 負の屈折率の概念から、自然界の物質には無い振る舞いをする人工物。
• 高屈折率高分子
• 偏光
• 粒子と波動の二重性

外部リンク

• わかりやすい高校物理の部屋 - 波の屈折
• 物理のかぎしっぽ - 屈折の法則
• 複屈折を測定できるPA/WPAシリーズの測定原理、装置構成、測定事例について（株）フォトニックラティス