束 (射影幾何学)

直線束?

数学とくに射影幾何学における束（そく、テンプレート:Lang-en-short, テンプレート:Lang-fr-shortテンプレート:Efn）は、初めデザルグによって、与えられた特定の一点を通る直線全体の成す族を幾何学的対象として捉えたものを指すものとして用いられた。

アポロニウスの円束

例

束の典型的なものは、射影平面上の二つの曲線 テンプレート:Math に対して二つの実数 テンプレート:Math を助変数とする曲線族

$\lambda C+\mu C^{\prime }=0$

として与えられる束である。この曲線の束に属する曲線は テンプレート:Math と テンプレート:Math との比 テンプレート:Math ごとに一つ定まる。テンプレート:Math を射影平面上の点の斉次座標と看做せば、対応する非斉次座標に関して テンプレート:Math または テンプレート:Mvar のいずれか一方は無限遠にある。

円束の例: 円束 テンプレート:Math に属する円をいくつかの テンプレート:Mvar について示したもの。これらの円はすべて、円 テンプレート:Math と直線 テンプレート:Math との交点を通る。直線 テンプレート:Math は無限遠点に対応するため、対応する テンプレート:Mvar に有限な値は定まらない。

例えば二直線 テンプレート:Math が有限領域内に交点を持てば、束 テンプレート:Math がその交点を通る直線の一群であることはすぐに判る。これを テンプレート:Mvar に関する直線束と呼ぶ。二直線の交点が無限遠にある（つまり二つの直線が平行である）とすれば、対応する直線束はその平行な二直線に平行な直線たちからなる。

また例えば、テンプレート:Math が交点を持つ二つの円ならば、束 テンプレート:Math は二円の交点をとおる円の集まりであり、テンプレート:Mvar に関する円束という。

あるいは一般に

${\lambda }_0{C}_0+{\lambda }_1{C}_1+\cdots +{\lambda }_k{C}_k=0$

を テンプレート:Math に関する テンプレート:Mvar-次の束 テンプレート:Lang と呼ぶ。

与えられた一直線を通る平面の全体の成す族である平面束はしばしば扇 テンプレート:Lang と呼ばれるテンプレート:Efn。

• 
  平面上の直線束はあたかも筆先を合わせた鉛筆の如くである。
• 
  一点から放射する半直線の束
• 
  一点に入射する半直線の束
• 
  無限遠を通る直線の束は平行線の族を成す
• 
  二点で交わる二円の交点を通る円束
• 
  一点で接する二円の交点を通る円束には半径無限大の円として二円の共通接線を通る直線を含む
• 
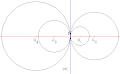
  交わりを持たない二円には根軸の上に中心を持つ円の束が対応する
• 
  三円に関するアポロニウスの円

関連項目

• テンプレート:Ill2
• 線型基本図形

外部リンク

• テンプレート:MathWorld
• テンプレート:PlanetMath