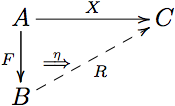Kan拡張

テンプレート:出典の明記 圏論においてカン拡張（カンかくちょう、Kan extension）とは普遍性を持つ構成の一種である。 カン拡張は随伴関手と近い関係を持つばかりでなく、圏における極限概念やエンドとも関係している。カン拡張の名は1960年に極限を用いてこの拡張を構成した ダニエル・カンの名に由来している。黎明期のカン拡張はホモロジー代数で導来関手を求める際に使われていた。 圏論の基礎（ ソーンダース・マックレーン 著）においてMac Laneは「すべての概念はカン拡張である」と述べ、さらには「カン拡張には圏論における基本的な概念がすべて含まれている」とまで述べている。

ある部分集合上で定義された関数を全体集合にまで拡張する操作を一般化したものがカン拡張である。カン拡張の定義は、当然のように高度に抽象化されている。特別な場合として、半順序集合の場合には、カン拡張は'constrained optimization'の問題となり比較的馴染み深いものになる。

定義

3つの圏

$𝐀,𝐁,𝐂$

および二つの関手

$X:𝐀\to 𝐂,F:𝐀\to 𝐁$,

が与えられたとき、$F$に沿った$X$のカン拡張は「左」カン拡張と「右」カン拡張の2種類がある。

どちらも、次の図式の破線で書かれた関手と2-セル$\eta$を見つけることに相当する。

形式的には、$X$の$F$に沿った右カン拡張とは関手$R:𝐁\to 𝐂$と自然変換$\eta :RF\to X$で余普遍性をもつもののことをいう。これは、任意の関手$M:𝐁\to 𝐂$と自然変換 $\mu :MF\to X$に対して、自然変換$\delta :M\to R$が一意的に定まって次の図式を可換にすることを意味する。

(ここで、${\delta }_F$は各$a\in 𝐀$に対して、コンポーネント${\delta }_F(a)=\delta (Fa):MF(a)\to RF(a)$を持つ自然変換である)

関手Rはしばしば${\mathrm{Ran}}_{F}X$と書かれる。

圏論におけるほかの普遍的構成と同じようにして、「左」カン拡張は右カン拡張の双対概念として得られる。すなわち上記の自然変換たちの向きを単に逆にするだけである。(関手$F,G:𝐂\to 𝐃$の間の自然変換 $T$は、$𝐂$の任意の対象$a$に対して、「自然な」性質を満たす射 $T(a):F(a)\to G(a)$で定まっていることに注意する。双対圏に変えるとき、$T(a)$のドメインと余ドメインが取り替えられて、$T$は逆の方向に働くのである)。

つまり右カン拡張と同様にして次のように述べられる: $X$の$F$に沿った左カン拡張とは関手 $L:𝐁\to 𝐂$ と自然変換$ϵ:X\to LF$で普遍性をもつもののことをいう。これは、任意の関手$M:𝐁\to 𝐂$と自然変換 $\alpha :X\to MF$に対して、自然変換$\sigma :L\to M$が一意的に定まって次の図式を可換にすることを意味する。

(ここで、${\sigma }_F$は各$a\in 𝐀$に対して、コンポーネント${\sigma }_F(a)=\sigma (Fa):LF(a)\to MF(a)$を持つ自然変換である)

そして関手Lはしばしば${\mathrm{Lan}}_{F}X$と書かれる。すべての普遍的構成と同様に、カン拡張も同型を除いて一意に定まる。左カン拡張の場合に関して言えば、もし$L,M$のふたつが$X$の$F$に沿った左カン拡張で、$ϵ,\alpha$が上記の自然変換だとするとき、図式を可換にするような関手の同型$\sigma :L\to M$が一意に存在するのである。右カン拡張の場合も同様である。

性質

（余）極限としてのカン拡張

$X:𝐀\to 𝐂$と$F:𝐀\to 𝐁$を関手とする。Aが小さい圏でCは余完備である場合は、$X$の$F$に沿った左カン拡張${\mathrm{L}\mathrm{a}\mathrm{n}}_{F}X$が存在して、Bの各対象bに対して

$({\mathrm{L}\mathrm{a}\mathrm{n}}_{F}X)(b)=\underset{f:Fa\to b}{\underrightarrow{\lim }}X(a)$

により定義される。ただし余極限はコンマ圏 $(F\downarrow b)$の上で取られるとする。

双対的にAが小さい圏で Cが完備ならば、 $X$の$F$に沿った右カン拡張が存在し、極限として求められる。

（余）エンドとしてのカン拡張

2つの関手

$K:𝐌\to 𝐂$ と $T:𝐌\to 𝐀$

は、Mの任意の対象mとm' およびCの任意の対象cに対して、A上の余冪$𝐂(K{m}^{\prime },c)\cdot Tm$を持つとする。さらに以下の余エンドが任意のCの対象cに対して存在すれば、関手TはKに沿った左カン拡張Lを持ち、Cの任意の対象cに対し、

$Lc=({\mathrm{L}\mathrm{a}\mathrm{n}}_{K}T)c={\int }^m𝐂(Km,c)\cdot Tm$

が成立する。

双対的に、右カン拡張も次の公式で計算できる。

$({\mathrm{R}\mathrm{a}\mathrm{n}}_{K}T)c=\underset{m}{\int }T{m}^{𝐂(c,Km)}$.

カン拡張としての（余）極限

関手$F:C\to D$の極限はカン拡張で表現できる。

$\mathrm{l}\mathrm{i}\mathrm{m}F={\mathrm{R}\mathrm{a}\mathrm{n}}_{E}F$

ここで、$E$は$C$から1（1つの対象と1つの射からなる圏、$Cat$の終対象）への一意的な関手とする。

$F$の余極限も同様に

$\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{m}F={\mathrm{L}\mathrm{a}\mathrm{n}}_{E}F$.

で表される。

参考文献

• テンプレート:Cite book
• テンプレート:Cite book