Newell の車両追従モデル

Newell の車両追従モデル(英: Newell’s car-following model) は車両の運転挙動を再現する交通流理論でのモデルの一つである。 車両は車頭距離が小さいときに減速し、十分な車頭距離がある場合は最高速度で走行するという運転挙動を以下の式によって表している。$$v=\{\begin{array}{cc}u& s>u\tau +\delta \\ \frac{s-\delta }{\tau }& s\le u\tau +\delta \end{array}$$ここで、$s$は車頭距離、$v$は現在速度、$u$は自由流速度、$\tau$は反応時間、$\delta$は停車時車頭距離である。

概要

本モデルは、マクロ交通流理論における三角形Fundamental Diagram をミクロ的に解釈したものになる。車頭距離$s$と密度$k$には以下の関係が成立する。

$k=\frac{1}{s}$

追従状態を仮定するとき、密度$k$は、速度$v$を用いて表現することもできる。$$\begin{array}{cc}k& =\frac{1}{s}\\ & =\frac{1}{u\tau +\delta }\\ & =\frac{\frac{1}{\tau }}{u+\frac{\delta }{\tau }}\\ & =\frac{\frac{1}{\delta }\frac{\delta }{\tau }}{u+\frac{\delta }{\tau }}\\ & =\frac{\kappa \omega }{u+\omega }\end{array}$$このとき、$\kappa$は渋滞密度、$\omega$は後進波速度である。渋滞密度と停車時車頭距離の間には以下の関係が成立する。

$\kappa =\frac{1}{\delta }$

また、後進波速度と停車時車頭距離、反応時間の間には以下の関係が成立する。

$\omega =\frac{\delta }{\tau }$

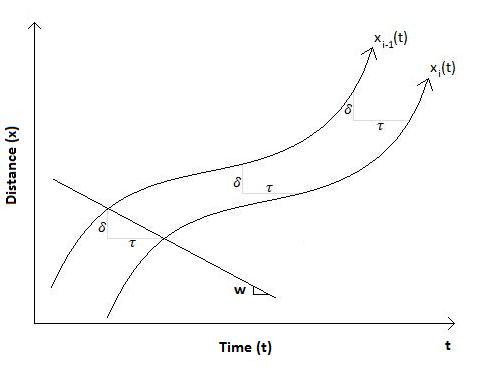
時空間図において、追従状態では先行車両と追従車両の車両軌跡は、時間的に$\tau$だけ遅れ、空間的に$\delta$だけ戻ったような軌跡が得られる。

すなわち、以下の等式が成立する。

$x_i(t)=x_{i-1}(t-\tau )-\delta$

追従状態ではない、すなわち自由流状態の場合車両の速度は自由流速度になる。そのため、車両 $i$ の車両軌跡は以下のように計算できる。

$x_i(t)=\min (x_i^F(t),x_i^C(t))$

このとき、車両 $i$ が自由流状態の場合実現する位置 $x_i^F(t)$は以下のようになる。

$x_i^F(t)=x_i(t-\mathrm{\Delta }t)+u\mathrm{\Delta }t$

ただし、$\mathrm{\Delta }t$ は任意の正の実数である。

車両 $i$ が追従状態の場合実現する位置 $x_i^C(t)$は以下のようになる。

$x_i^C(t)=x_{i-1}(t-\tau )-\delta$

$\mathrm{\Delta }t=\tau$ が成立する場合、計算が容易である。このような車両の位置を計算するモデルはXモデルと呼ばれる。

ドライバーの攻撃性

現実世界の状況では、後続車両の不適切な運転挙動により、本モデルで予測される車両軌跡軌道と異なる可能性がある。実際に得られた車両軌跡と、理論的な車両軌跡を比較し、車両異質性を明らかにできる。次の図は、実際の車両軌跡 (黒) と、本モデルによって予測された後続車両の車両軌跡 (青) を示している。

後続車両の運転挙動が理論と一致する場合の車両軌跡図

後続車両の運転挙動が注意深い場合の車両軌跡図

後続車両の運転挙動が注意散漫な場合の車両軌跡図

後続車両の反応時間と停車時車頭距離が長い場合、先行車両と後続車両の車両軌跡の差が大きくなる。これは、後続車両の注意深い運転を意味する。一方、反応時間と停車時車頭距離が短い場合、先行車両と後続車両の車両軌跡の差が小さくなる。これは、後続車両は攻撃的な運転を意味する。