定圧過程

テンプレート:出典の明記 {{#invoke:Sidebar |collapsible | bodyclass = plainlist skin-invert-image | titlestyle = padding-bottom:0.3em;border-bottom:1px solid #aaa; | title = 熱力学 | imagestyle = display:block;margin:0.3em 0 0.4em; | image = | caption = 古典的テンプレート:仮リンク | listtitlestyle = background:#ddf,;text-align:center;color: light-dark(black,white); | width = 256px | expanded =

| list1name =branches | list1title = 分野 | list1 = テンプレート:Startflatlist

• 熱力学
• 統計力学
• 熱化学

• 平衡熱力学テンプレート:\非平衡熱力学

| list2name = laws | list2title = 熱力学の法則 | list2 = テンプレート:Startflatlist

• 第零法則
• 第一法則
• 第二法則
• 第三法則

| list3name = systems | list3title = 系 | list3 =

テンプレート:Sidebar

| list4name = sysprop | list4title =系の特性

| list4 =

注: 斜体はテンプレート:仮リンクを示す。

テンプレート:Sidebar

| list5name = material | list5title = テンプレート:仮リンク | list5 =

比熱容量	$c=$	$T$ $\partial S$ $N$ $\partial T$
圧縮率	$\beta =-$	$1$ $\partial V$ $V$ $\partial p$
熱膨張	$\alpha =$	$1$ $\partial V$ $V$ $\partial T$

| list6name = equations | list6title = テンプレート:仮リンク | list6 = テンプレート:Startflatlist

• カルノーの定理
• クラウジウスの定理
• テンプレート:仮リンク
• 理想気体の状態方程式
• マクスウェルの関係式
• オンサーガーの相反定理
• テンプレート:仮リンクテンプレート:Endflatlist

| list7name = potentials | list7title = 熱力学ポテンシャル | list7 = テンプレート:Startflatlist

• 自由エネルギー
• テンプレート:仮リンク

| list8name = hist/cult | list8title = テンプレート:Hlist | list8 =

テンプレート:Sidebar

| list9name = scientists | list9title = 科学者 | list9 = テンプレート:Startflatlist

• ベルヌーイ
• ボルツマン
• カルノー
• クラペイロン
• クラウジウス
• カラテオドリ
• デュエム
• ギブズ
• フォン・ヘルムホルツ
• ジュール
• マクスウェル
• フォン・マイヤー
• オンサーガー
• ランキン
• スミートン
• シュタール
• トンプソン
• トムソン
• ファン・デル・ワールス
• ウォーターストン

| below =

}} 定圧過程（ていあつかてい）あるいは等圧過程（とうあつかてい、テンプレート:Lang-en-short）とは、一定の外圧の下で、気体や液体など流体の系をある状態から別の状態へと変化させる熱力学的な過程である。状態を遷移する間に系が外部に行う仕事は状態量ではないため、遷移が準静的ではない場合には一般に求めることはできないが、等圧過程においては準静的な遷移でなくとも仕事を求めることができる。

概要

等圧過程とは外圧が一定であるという条件であり、外界との釣合いの条件は要求されない。そのため、等圧過程で状態を遷移する間で系は内部に流動がある非平衡状態を取り得る。流動がある場合には流体力学に基づいて系の内圧は場として記述されるため、内部で定まった大きさを持つ熱力学的な状態量としての圧力は定義されない。しかし、体積変化に伴って系が外部に行う仕事は系の境界での圧力によって定まるため、内部の状態にかかわらず、外圧が既知であれば仕事を求めることができる。系が外部に及ぼす圧力は、作用・反作用の法則により、外部から系に及ぼされる外圧と等しい。したがって、外圧 テンプレート:Math の下で体積の変化が テンプレート:Mvar のとき、体積変化に伴って系が外部に行う仕事は テンプレート:Indent で与えられる。

熱力学第一法則から、閉鎖系が状態を遷移する間に外部から流入する熱 テンプレート:Mvar は、系が外部に行う仕事 テンプレート:Mvar と、状態を遷移する前後での内部エネルギーの変化 テンプレート:Mvar との間に テンプレート:Math の関係にあるため、系が体積変化に伴う仕事以外で外部に仕事を行わない場合には テンプレート:Indent となり、エンタルピーを導入すれば テンプレート:Indent となる。

定積モル比熱と定圧モル比熱の関係

図の黄色の面積がW=PΔVとなる。

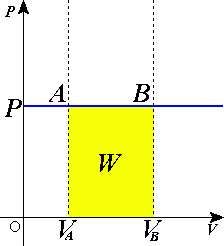
理想気体を状態Aから状態Bに移行させる定積過程を考える。熱力学第一法則より

$\begin{array}{c}\mathrm{\Delta }U=Q-W\end{array}$

ここでΔUは系の内部エネルギーの変化、Qは系に与えられた熱量、Wは系が外にした仕事である。

定圧過程では圧力が一定なので

$\begin{array}{c}W=F\mathrm{\Delta }x=PS\mathrm{\Delta }x=P\mathrm{\Delta }V\end{array}$

が成り立つ。

従って熱力学第一法則の式は

$\begin{array}{c}\mathrm{\Delta }U=Q-P\mathrm{\Delta }V\end{array}$

となるので熱量Qは

$\begin{array}{c}Q=\mathrm{\Delta }U+P\mathrm{\Delta }V\end{array}$

と表される。

ここで、定圧過程におけるモル比熱を定圧モル比熱と名付け、$c_P$とすると比熱の定義より

$\begin{array}{c}Q=n{C}_P\mathrm{\Delta }T\end{array}$

となる。従って

$\begin{array}{c}n{C}_P\mathrm{\Delta }T=\mathrm{\Delta }U+P\mathrm{\Delta }V\end{array}$

ここで理想気体の状態方程式より

$\begin{array}{c}(P+\mathrm{\Delta }P)(V+\mathrm{\Delta }V)=nR(T+\mathrm{\Delta }T)\end{array}$

が成り立つ。定圧過程では$\mathrm{\Delta }P=0$なので、上の式を整理すると

$\begin{array}{c}P\mathrm{\Delta }V=nR\mathrm{\Delta }T\end{array}$

となる。また定積モル比熱$c_V$を用いるとΔUは

$\begin{array}{c}\mathrm{\Delta }U=n{C}_V\mathrm{\Delta }T\end{array}$

となる。これらを先に求めた式に代入すると

$\begin{array}{c}n{C}_P\mathrm{\Delta }T=n{C}_V\mathrm{\Delta }T+nR\mathrm{\Delta }T\end{array}$

従って定圧モル比熱と定積モル比熱の間には次の関係が成立する。

$\begin{array}{c}{C}_P=C_V+R\end{array}$

この関係をマイヤーの法則という。

関連項目

• ランキンサイクル - 復水器
• 定積過程
• 等温過程
• 断熱過程
• 可逆
• 比熱