コンコイド

コンコイド
本文の式でa=1,l=1のとき

コンコイド
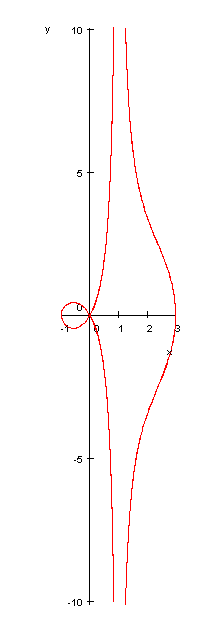
本文の式でa=1,l=2のとき

コンコイド（conchoid）は直交座標の方程式

$(x-a{)}^2(x^2+y^2)-l^2{x}^2=0$

によって表される曲線である。古代ギリシアの数学者テンプレート:仮リンクにちなんでニコメデスのコンコイドとも呼ばれる。

器具を用いたニコメデスのコンコイドの書き方（アスカロンのエウトキオスによるアルキメデス『球と円柱について』の註解に説明がある）

名称

当初は、形がムラサキイガイ (テンプレート:Lang-grc-short) に似ていることから、コクロイド (cochloid, テンプレート:Lang-grc-short) と呼ばれていた。しかし、やがてコンコイド (conchoid, テンプレート:Lang-grc-short) と呼ばれるようになった。

性質

パラメータ表示では

$x=a+l\cos \theta ,y=a\tan \theta +l\sin \theta$

と表される。 極座標の方程式では

$r=\frac{a}{\cos \theta }+l$

と表される。

x軸に対して線対称である。x=aを漸近線に持つ。

参考文献

• 『曲線の事典 性質・歴史・作図法』　礒田正美、Maria G. Bartolini Bussi編、田端毅、讃岐勝、礒田正美著

共立出版、2009年　ISBN 9784320019072

外部リンク

• テンプレート:Kotobank