ジグザグ補題

数学、特にホモロジー代数学におけるジグザグ補題（ジグザグほだい、テンプレート:Lang-en-short）は、鎖複体のホモロジー群から成るある種の長完全列の存在を述べるものである。この結果は任意のアーベル圏で通用する。

補題の主張

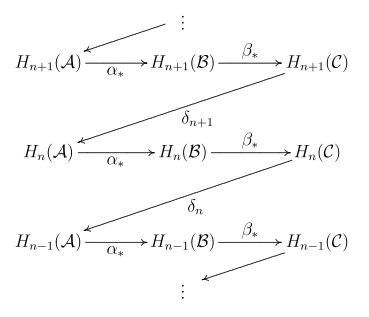
任意のアーベル圏（アーベル群の圏や与えられた体上のベクトル空間の圏など）において、$(𝒜,{\partial }_{\bullet }),(ℬ,{\partial }_{{\bullet }^{\prime }}),(𝒞,{\partial }_{{\bullet }^{″}})$ が以下の短完全列を満たす鎖複体だとする：

$0⟶𝒜\stackrel{\alpha }{⟶}ℬ\stackrel{\beta }{⟶}𝒞⟶0$

この系列は以下の可換図式の略記であるとする：

ここで各行は全て完全で、各列は全て鎖複体である。

ジグザグ補題は、境界写像（族）

${\delta }_n:H_n(𝒞)⟶H_{n-1}(𝒜),$

が存在して、次の系列を完全にすることができることを主張する：

${\alpha }_{*}^{}$ と ${\beta }_{*}^{}$ は、通常のやり方で誘導されたホモロジー群の間の写像である。境界写像 ${\delta }_n^{}$ は以下の節で説明する。この補題の名称は、系列における写像が「ジグザグ」に走ることから来ている。不運な用語法のバッティングにより、ホモロジー代数には『蛇の補題』の名を持つ別の結果があるにもかかわらず、この命題（ジグザグ補題）はその名（蛇の補題）でも一般に知られている。蛇の補題を使うと、ジグザグ補題のここに記すものとは別の証明が得られる。

境界写像の構成

写像 ${\delta }_n^{}$ は標準的な図式追跡の議論を使って定義できる。$c\in C_n$ を、 $H_n(𝒞)$ に属すある同値類の代表元とする。よって ${{\partial }_n}^{″}(c)=0$ 。行方向の完全性より ${\beta }_n^{}$ は全射なので、${\beta }_n^{}(b)=c$ となる $b\in B_n$ が存在しなければならない。図式の可換性より、

${\beta }_{n-1}{{\partial }_n}^{\prime }(b)={{\partial }_n}^{″}{\beta }_n(b)={{\partial }_n}^{″}(c)=0$

再び行方向の完全性より、

${{\partial }_n}^{\prime }(b)\in \ker {\beta }_{n-1}=\mathrm{i}\mathrm{m}{\alpha }_{n-1}$

${\alpha }_{n-1}^{}$ は単射だから、${\alpha }_{n-1}(a)={{\partial }_n}^{\prime }(b)$ を満たす $a\in A_{n-1}$ が一意的に存在する。これは輪体である。なぜなら ${\alpha }_{n-2}^{}$ は単射で、かつ ${\partial }^2=0$ より

${\alpha }_{n-2}{\partial }_{n-1}(a)={\partial }_{n^{\prime }-1}{\alpha }_{n-1}(a)={\partial }_{n^{\prime }-1}{{\partial }_n}^{\prime }(b)=0$

が従うからである（つまり ${\partial }_{n-1}(a)\in \ker {\alpha }_{n-2}=\{0\}$ ）。$a$ は輪体なので、$H_{n-1}(𝒜)$ に属すある同値類の代表元になる。ここで、

${\delta }_{}^{}[c]=[a]$

と定義する。このように定義された境界写像は well-defined であることが示せる（つまり写像が c と b の選択に依らずに定まる。証明は上記の図式追跡の議論と同様である）。また同様の議論で、長系列が各ホモロジー群のところで完全であることも示せる。

関連項目

• マイヤー・ヴィートリス完全系列

参考文献

• テンプレート:Cite book
• テンプレート:Lang Algebra
• テンプレート:Cite book