ヌルベクトル

A null cone where n = 3

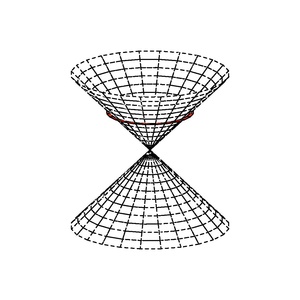
数学において二次空間 テンプレート:Math（すなわち二次形式 テンプレート:Mvar を備えたベクトル空間 テンプレート:Mvar）のヌルベクトル (null vector) または等方ベクトル（とうほうベクトル、テンプレート:Lang-en-short）とは、テンプレート:Math を満たす非零元 テンプレート:Math を言う。

実二次形式の理論において、定符号二次形式と等方二次形式は相異なる（両者の違いは後者には非零ヌルベクトルが存在するという点だけである）。そのようなベクトルが取れるとき、二次空間 テンプレート:Math はテンプレート:仮リンクと呼ばれる。擬ユークリッドなベクトル空間 テンプレート:Mvar は、（一意とは限らない）互いに直交する部分空間 テンプレート:Mvar を用いて テンプレート:Math と分解して、二次形式 テンプレート:Mvar が テンプレート:Mvar 上正定値かつ テンプレート:Mvar 上負定値となるようにすることができる。テンプレート:Mvar のヌル円錐または等方錐は均衡球面の合併 $$\bigcup _{r\ge 0}\{x=a+b:q(a)=-q(b)=r,a\in A,b\in B\}$$ からなる。この錐は原点を通るテンプレート:仮リンクすべての合併でもある。

例

• ミンコフスキー空間の光的ベクトルはヌルベクトルである。
• 四つの線型独立なテンプレート:仮リンク テンプレート:Math, テンプレート:Math, テンプレート:Math, テンプレート:Math はヌルベクトルで テンプレート:Math は時空を表すのに用いられる部分空間の基底を与える。ヌルベクトルは時空多様体に対するテンプレート:仮リンクにも利用される。
• 合成代数はヌルベクトルを持つとき分解型 (split) であり、さもなくば多元体である。
• リー代数のテンプレート:仮リンクにはヌルベクトルが存在する。

参考文献

• テンプレート:Cite book
• テンプレート:Cite book
• テンプレート:Cite book

外部リンク

• テンプレート:MathWorld