公平性 (機械学習)

機械学習における公平性（こうへいせい、テンプレート:Lang-en-short）は、機械学習モデルを用いた自動意思決定の過程でのアルゴリズムバイアスを是正する取り組みのことを指す。機械学習のプロセスを経たコンピュータによる意思決定が機微なテンプレート:仮リンクに基づいている場合、そのような意思決定は不公平とみなされる場合がある。機微な変数の具体例には、性別、民族、性的指向、障害の有無などが挙げられる。他の多くの倫理的な概念と同様に、公平性やバイアスの定義は常に論争の的となってきた。一般に、意思決定が人々の生活に影響を与える場合、公平性やバイアスの問題が重要になってくると考えられる。機械学習の分野では、アルゴリズムバイアスの問題はよく知られており、広く研究の対象となっている。結果は多様な要素によって歪められ、特定の集団や個人にとって不公平とみなされる場合がある。このような事例の例として、ソーシャルメディアサイトがパーソナライズされたニュースを消費者に配信する場合などが挙げられる。

背景

機械学習における公平性の議論は比較的最近の論点である。2016年からその論点における研究で急な増加があった^[1]。この増加はある程度アメリカ合衆国の裁判所で累犯を予測するのに広く用いられる、 COMPASソフトウェアが、人種上のバイアスであること主張するところの、プロパブリカによる影響力のある報告とみなされる^[2]。一つの研究の論点および議論は、機械学習のモデルを判断するには困難にさせるものである、普遍性をもった定義は無くそして異なった定義はたがいに矛盾しうるものとしての、公平性の定義である^[3]。他の研究の論点は、発生論（テンプレート:Lang-en-short）、類型論（テンプレート:Lang-en-short）、および低減方法論（テンプレート:Lang-en-short）を含む^[4]。

近年高度な技術を持った企業は機械学習でのバイアスの探知と低減の方法に関する道具（ソフトウェアツール、略してツール）と取扱書をつくらせた。ソフトウェアバイアスを低減しその公平性を上昇させる特別なアルゴリズムをもったPythonとR言語のツールをIBMは持っている^[5]^[6]。Googleは機械学習でのバイアスを研究し撃退する指針とツールを発表した^[7]^[8]。フェイスブックは彼らのツールの利用、公平性の流れ（テンプレート:Lang-en-short）、彼らの人工知能でのバイアスの探知を報告した^[9]。しかしながら、それら企業の努力は十分でなく、そのような従業員によるツールの少しの利用を報じることは、ツールの利用が選択的であっても、そしてそれが可能であっても、すべての彼らのプログラムにたいして使うことはできないことを、論評者たちは主張した^[10]。

論争

テンプレート:Main 法律上のシステムでのアルゴリズム的な意思決定の利用は、吟味のもとでの利用での注目に値する領域でありつづけてきた。2014年に、アメリカ合衆国司法長官エリック・ハンプトン・ホルダーは、「リスクアセスメント」の方法が、被告の教育水準や社会経済的背景のような、彼らの管理の下ではない要因に過度に焦点をあてさせるかもしれないという問題を提起した^[11]。COMPASに関するプロパブリカによる2016年の報告は、黒人の被告が白人の被告よりもたいてい二度高リスクとして誤って分類される可能性が高く、これに対して白人において逆の誤りがなされることを主張した^[2]。COMPASの製作者の、Northepointe Inc.は、彼らのツールが公正でプロパブリカが統計的誤りをしたことを主張して、その報告と争った^[12]。これは引き続きプロパブリカにより再度反論された^[13]。

集団公平性規準

分類問題において、アルゴリズムは、既知の特性 $X$ から、目的の変数である、離散的な特性 $Y$ を予測する関数を学習する。 $A$ を、含まれた幾つかの特性を変換するかまたは、機微な特性（性別、民族、性的指向、その他）として考える $X$ において'陰的に'（テンプレート:Lang-en-short）変換するものである、離散的な確率変数とする。最後に、分類子（テンプレート:Lang-en-short）の予測を $R$ で記す。今、幾つかのこれら機微な変数によって影響されない予測であるかどうか、与えられた分類子が公平であるならば、三つの主な評価規準を定義する^[14]。

独立性

確立変数 $(R, A)$ が、もしその機微な特性変数 $A$ が予測子 $R$ と確率的に独立であるとき、独立性を満たすと呼び、 $R ⊥ A .$ と記す。この記法は次の式でも表すことができる： $P (R = r | A = a) = P (R = r | A = b) \forall r \in R \forall a, b \in A$ これは、各々の目的クラスの分類比率は機微な特性変数 $A$ を尊重する異なった集団に属する人々に等しいことを意味する。

分離性

確立変数 $(R, A, Y)$ が、もしその機微な特性変数 $A$ が目的変数 $Y$ によって与えられる予測子 $R$ と確率的に独立であるとき、分離性を満たすと呼び、 $R ⊥ A | Y .$ と記す。この記法は次の式でも表すことができる： $P (R = r | Y = q, A = a) = P (R = r | Y = q, A = b) \forall r \in R q \in Y \forall a, b \in A$ これは、機微な属性 $A$ に関する判別 $R$ のすべての独立性は真の目的変数 $Y$ の実際の独立性と一致されなくてはならないことを意味する。

充分性

確立変数 $(R, A, Y)$ が、もしその機微な特性変数 $A$ が予測子 $R$ によって与えられる　目的変数 $Y$ と確率的に独立であるとき、充分性を満たすと呼び、 $Y ⊥ A | R .$ と記す。この記法は次の式でも表すことができる： $P (Y = q | R = r, A = a) = P (Y = q | R = r, A = b) \forall q \in Y r \in R \forall a, b \in A$

定義の間の関係

上記に与えた三つの定義に関する主要な結果を要約すると：

$Y$ が二値判別的であることを考えると、もし $A$ と $Y$ が独立でなく、かつ $R$ と $Y$ が独立でもなければ、独立性と分離性はともに保たれない。
もし同時分布としての $(R, A, Y)$ がすべてのそのとりうる値についての'陽確率'（テンプレート:Lang-en-short）をもち、かつ $A$ と $Y$ が独立でないならば、分離性と充分性はともに保たれない。

集団公平性の定義の数学的定式化

基本定義

テンプレート:Main

公平性の統計的測定の多くは異なった計測にあるので、それらを定義することから始める。二値の分類による作業の場合、予測のものと実際の両方の分類は二つの値をとり得る：陽値と陰値。予測と実際の結果の間の、異なった可能な関係の説明から今始める^[15]：

テンプレート:Clear

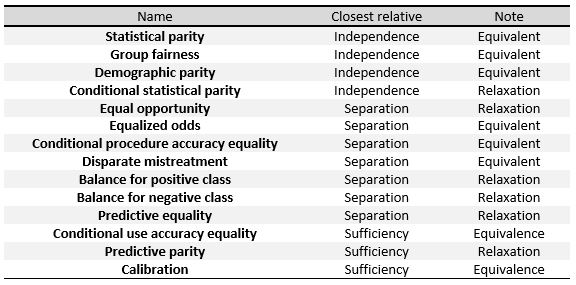
次の規準はこの節の最初の、独立性、分離性、充分性の三つの主な定義の計測として理解できる。右の表において、それらの間の関係をみることができる。

予測結果に基づく定義

この節における定義は客体の多様な確率分布についての予測結果 $R$ に焦点をあてる。これらは最も単純で最も直接的な公平性の記述である。

統計的平価（テンプレート:Lang-en-short）、承認（または容認^[16]）比率平価（テンプレート:Lang-en-short）または比較分析（テンプレート:Lang-en-short）とも呼ばれる、人口統計的平価（テンプレート:Lang-en-short）。もし保護ならびに非保護の集団での客体が陽評価への割り当てへ等確率であるならば、分類子はこの定義を満足する。これは、次式を満足する場合である：

$P (R = + | A = a) = P (R = + | A = b) \forall a, b \in A$

予測と実際の結果に基づく定義

これらの定義は予測結果 $R$ だけでなく、それを実際の結果 $Y$ と比較することも考慮する。

全体精度平等（テンプレート:Lang-en-short）。保護ならびに非保護の集団における客体が等予測精度を有するならば、分類子はこの定義を満たす。これは、ひとつの分類からの客体の確率がそれに承認される。これは次式を満足する場合である：

$P (R = Y | A = a) = P (R = Y | A = b) \forall a, b \in A$

予測された確率と実際の結果に基づく定義

これらの定義は実際の結果 $Y$ とその予測された確率得点 $S$ に基づく。

較正（テンプレート:Lang-en-short）、または条件の度数の突合せ（テンプレート:Lang-en-short）とも呼ばれる、検査公平性（テンプレート:Lang-en-short）。諸個人が保護または非保護の集団のどちらかに属するときに、同一の予測確率得点 $S$ をもつ彼ら個人が同一の陽分類での分類になる確率を有するならば、分類子はこの規準を満たす：

$P (Y = + | S = s, A = a) = P (Y = + | S = s, A = b) \forall s \in S \forall a, b \in A$

社会的厚生関数

何人かの学者はアルゴリズム的公平の定義を社会的厚生関数の術語で提示した。社会的厚生関数の使用は、アルゴリズムによって影響を受ける人々についての効用の用語をもって、アルゴリズムの設計者に公平性を考慮にいれ正確さを予測するようにさせることを彼らは主張する。それは設計者に原則的な方法での効率性と公平性（テンプレート:Lang-en-short）の一得一失をさせる^[17]。アルゴリズム設計者は恵まれない集団の絶対的な利得を認識するために社会的厚生関数を使うべきであることをテンプレート:仮リンクは述べた。例えば、犯罪の割合が一定である間も、純粋に人間による判定（テンプレート:Lang-en-short）よりも、黒人、ヒスパニック、など人種的少数派全般に対する拘留率を引き下げる、未決拘禁での意思決定アルゴリズムを使う研究が見られる^[18]。

個別公平性規準

公平性の定義における重要なひとつ大きな差異は集団と個別の概念の間のものである^[19] ^[20]^[15]^[21]。率直にいえば、集団公平性規準が、たいてい機微属性（たとえば、性別、民族、年齢、その他…）によって識別する、集団水準で数量比較するのに対し、個別規準は諸個人を比較する。言い換えれば、その規準は「似通った諸個人は似通った処理をすべきである」ことに従う。

不知を通した公平性（テンプレート:Lang-en-short、略してFTU）と通常称されるもの、あるいは（自動的な）決定を行う際に陽に機微特徴を用いないことを規定するものである、'無分別'（テンプレート:Lang-en-short）によるものである、公平性に対するとても直観的な取り組み方がある。二人の個人が、その同じ結果を受け入れるような彼らの機微属性の値についてだけ異なっているため、これは個別公平性の概念に有効である。

最も一般的な個別公平性の概念は2012年にテンプレート:日本語版にない記事リンクとその共同研究者らによる先駆的な仕事において導入された^[22]。そして、モデル写像におけるリプシッツ条件として表現される、入力としての特徴をとる決定写像が「似通った個人らは同じように写像する」ようにできることを組み立てられるべきであるところの原理の、ある数学的な翻訳として考えられる。彼らは、特定の状況でどの個人らが'似ている'かを査定することにおいて、適当な目的‐関係の距離計量の選択の重要性を強調したので、精確にはFTUとは対位法の、認識を通した公平性（テンプレート:Lang-en-short、略してFTA）と彼らはこの取り組み方を呼んだ。再び、この問題は、特定の文脈でいかなる変数が「正当」なものとして取り上げられうるかに関して持ち上がる論点にとても関連する。

因果関係にもとづく測定

因果性公平性（テンプレート:Lang-en-short）は、どちらのリソースの割り当てが公正な個人的な処理の受け入れに公平であるかの尊重をもった、特性の或る組み合わせにおいてだけ異なる者の、二つの似通った個々の利用者またはアプリケーションのものによる度数を測定する^[23]。公平性計測に関する学術的な研究の全部の分野は、機械学習モデルでの偏見を評価することに、因果性モデルを波及するよう発展してきた。この対処法は通常、同一に観測されるデータの分布は作用における変数の間の、ひょっとすると偏見のなんらかの形によって結果が影響されているか否かの違った表現の、違った因果性関係を隠しているかもしれない事実によって、根拠を示す^[14]。

テンプレート:Harvはテンプレート:仮リンク（テンプレート:Lang-en-short）を用いることを提案する、そしてもし任意の個人について、機微情報が変化したときに反事実シナリオにおいて結果が変化しなければ、意思決定過程の反事実公平性（テンプレート:Lang-en-short）が満たされるものとして定義する。その数学的な定式化は次式を導く：　 $P (R_{A \leftarrow a} = 1 | A = a, X = x) = P (R_{A \leftarrow b} = 1 | A = a, X = x), \forall a, b;$

ここに：機微属性が $A = a$ でその他の特徴が $X = x$ であるランダムな個人と、 $A = b$ を有する同じような個人について、彼らは承認になる機会が同じになるべきであるとする。

バイアス軽減戦略

3つの異なった方法により機械学習アルゴリズムに公平性を施しうる：データ前処理、ソフトウェアの学習（テンプレート:Lang-en-short）における数理最適化、もしくはアルゴリズムの後処理の結果。

前処理

大抵、分類は単独では問題ではない；データセットも偏見化されている。 $A = a$ と尊重するデータセット $D$ の偏見は次のように定義される： $d i s c_{A = a} (D) = \frac{| {X \in D | X (A) \neq a, X (Y) = +} |}{| {X \in D | X (A) \neq a} |} - \frac{| {X \in D | X (A) = a, X (Y) = +} |}{| {X \in D | X (A) = a} |}$

再計量

再計量（テンプレート:Lang-en-short）は前処理アルゴリズムの一例である。その考え方は、指定された集団の尊重による計量された偏見が0になるように、各々のデータセットにある計量を割り当てることである^[24]。

センシティブ変数 $A$ をデータセット $D$ が差別せず、目的変数 $Y$ が独立で、同時分布の確率が次のような確率の積であるならば： $P_{e x p} (A = a \land Y = +) = P (A = a) \times P (Y = +) = \frac{| {X \in D | X (A) = a} |}{| D |} \times \frac{| {X \in D | X (Y) = +} |}{| D |}$

処理中に行う方法

別の対処法は学習時に偏見を直すことである。アルゴリズムの最適化をする目標に対して制約を課することによりこれはなされうる^[25]。保護された集団とその残りの個人らについての一定の測定の同じ比率を保つことによって、これらの制約はアルゴリズムに公平性を改善するようせしめる。たとえば、誤った陽割合が、保護された集団での個人と保護された集団の他のものとで同じになる、目標の条件をアルゴリズムに追加することができる。

この取り組み方でのおもに用いられる測定は誤った陽割合、誤った陰割合、及び全部の誤分類割合である。アルゴリズムの目標にこれら制約のたった一つもしくは幾つかを追加することができる。誤った陰割合の等しさは、これは機会の平等を意味するから、真の陽割合の等しさを意味することに注意せよ。問題についての制約を課したのち、解決しないかもしれない、そうなのでそれらにおける緩和が逆に必要かもしれない。

高精度に公平性を改善ことにおいてこのテクニックはよい結果を達成する、そして改善のための公平性の測定をプログラマーに選ばせる。しかしながら、各々の機械学習の作業は異なった適用可能な方法を必要とし、そして分類法での、常に可能とは限らないコードは修正が必要かもしれない^[26]。

突出した偏見の除去

同じ最急降下による方法（最急降下法を見よ）を通じて同時に二つの分類を矯正する。一つに、'予測器'（テンプレート:Lang-en-short）は、それの重み $W$ で修正された、何らかの損失関数 $L_{P} (\hat{y}, y)$ を最小化させる、 $X$ で与えられる入力の、目的変数の、 $Y$ の予測の作業を達成しようとする。二つに、'反対器'（テンプレート:Lang-en-short）は、なんらかの損失関数 $L_{A} (\hat{a}, a)$ を最小化するような、その重み $U$ で修正された $\hat{Y}$ が与えられ、機微変数の $A$ の予測を達成しようとする^[27]^[28]。

正確に進めるのに、ここで重要な点は、前述の $\hat{Y}$ は、その離散的な予測ではなく、分類法の生の出力を意味しているに違いないことである；たとえば、人工ニューラルネットワークや分類問題をもって、ソフトマックス層の出力を $\hat{Y}$ は意味する。

毎学習段階に勾配 $\nabla_{U} L_{A}$ に応じて $L_{A}$ を最小化するよう $U$ を更新し、次の式により $W$ を修正する： $\nabla_{W} L_{P} - p r o j_{\nabla_{W} L_{A}} \nabla_{W} L_{P} - α \nabla_{W} L_{A}$ ここに、 $α$ は毎段階で変化しうる、調整可能なテンプレート:仮リンクである。

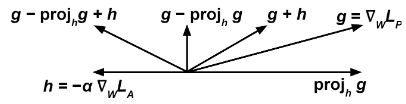
テンプレート:Harvnbで示されたような、突出した偏見の除去で用いられるベクトルの図示。

直観的な考えは、'反対器'が $\hat{Y}$ からの機微変数の予測に失敗するから、'予測器'が $L_{P}$ （すなわち $\nabla_{W} L_{P}$ ）を最小化をするときに、同時に、 $L_{A}$ （すなわち $- α \nabla_{W} L_{A}$ ）をも最大化させたいことである。テンプレート:Clear

後処理

最後の方法は公平を達成する分類の結果を修正することを試みる。この方法では、各々の個人に対する得点を返すような分類を用い、そしてそれらについての2値の推測（テンプレート:Lang-en-short）を必要とする。低得点が陰なものを得そうなのに対して、高得点は陽な結果を得そうにみえる、しかし、望む場合に然りと答えるように、その決定をするようなテンプレート:日本語版にない記事リンクを調整することができる。その閾値の値の変動は真の陽のものと真の陰のものにおける一得一失に影響を与えることに注意せよ。

選択的な分類を避けること

$P (+ | X)$ を、事例 $X$ が陽な分類＋に属するところの確率としての分類により計算される確率とするような、分類を考える。 $P (+ | X)$ が1もしくは0に近い場合、その事例 $X$ は一定の高い頻度をもって順に＋か－に属することをもって表される。けれども、 $P (+ | X)$ が0.5に近いならば分類が大きく不確かになる^[29]。

脚注

テンプレート:Reflist

引用文献

ウェブサイト

書籍

AV媒体

テンプレート:Cite AV media

雑誌

ウェブアーカイブ

[1] テンプレート:Harvnb

[:0-2] 2.0 ^2.1 テンプレート:Harvnb

[3] テンプレート:Harvnb

[4] テンプレート:Harvnb

[IBM-5] テンプレート:Harvnb

[6] テンプレート:Harvnb

[7] テンプレート:Harvnb

[8] テンプレート:Harvnb

[9] テンプレート:Harvnb

[10] テンプレート:Harvnb

[11] テンプレート:Harvnb

[12] テンプレート:Harvnb

[13] テンプレート:Harvnb

[Barocas-14] 14.0 ^14.1 テンプレート:Harvnb

[metrics_paper-15] 15.0 ^15.1 テンプレート:Harvnb

[16] "acceptace"の訳につき以下同じ。

[chen-hooker-2021-17] テンプレート:Harvnb

[18] テンプレート:Harvnb

[mitchell2021-19] テンプレート:Harvnb

[castelnovo2022-20] テンプレート:Harvnb

[mehrabi2021-21] テンプレート:Harvnb

[22] テンプレート:Harvnb

[causal-23] テンプレート:Harvnb

[reweighing-24] テンプレート:Harvnb

[zafar-25] テンプレート:Harvnb

[datascience-26] テンプレート:Harvnb

[adversarial1-27] テンプレート:Harvnb

[adversarial2-28] テンプレート:Harvnb

[roc-29] テンプレート:Harvnb

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

公平性 (機械学習)

目次

背景

論争

集団公平性規準

独立性

分離性