応力-ひずみ曲線

引張試験における典型的な塑性金属の応力-ひずみ曲線

応力-ひずみ曲線（おうりょく-ひずみきょくせん、テンプレート:Lang-en）とは、材料の引張試験、圧縮試験において得られる応力とひずみの関係曲線テンプレート:Sfnテンプレート:Sfn。応力-ひずみ線図（テンプレート:Lang-en）とも呼ばれるテンプレート:Sfn。

一般的に、ひずみを横軸に、応力を縦軸にとって描かれるテンプレート:Sfn。材料によって応力-ひずみ曲線は異なり、縦弾性係数、降伏点、引張強さといった、それぞれの材料の基礎的な機械的性質を応力-ひずみ曲線から得ることができるテンプレート:Sfnテンプレート:Sfn。

測定と用語

引張試験・圧縮試験

実際の引張試験の様子。真ん中の茶色の物体が測定対象の試料。

材料の応力-ひずみ曲線は、引張（ひっぱり）試験または圧縮試験によって調べられるテンプレート:Sfn。特に引張試験は機械的性質を調べるものとして最も一般な試験の一つであるテンプレート:Sfn。

材料に引張荷重を加えると、その材料は変形して引っ張る方向に伸び、圧縮すると縮む。この荷重値と変形量の関係を測定することにより、荷重-変形曲線を得ることができるテンプレート:Sfn。しかし、同じ荷重を加えても試料の太さによって伸びや縮み（変形）の量は異なるテンプレート:Sfn。同じ荷重で比較すると、太くなるほど伸びや縮みは少なくなる。このため、材料が受ける負荷を知るには、単位面積当たりの荷重である応力で評価した方が良いテンプレート:Sfn。材料に加える単軸荷重を F とし、F に直角な断面積を A とすれば、材料に加わる応力 σ は、

$\sigma =\frac{F}{A}$

で表されるテンプレート:Sfn。一方、同じ応力を加えても、試料の長さによって伸びや縮みの量は異なるテンプレート:Sfn。そのため、変形量そのものではなく、単位長さ当たりの伸びや縮みであるひずみで変形の程度を評価するテンプレート:Sfn。試料の初期長さを L₀ とし、初期状態からの伸びを λ とすると、ひずみ ε は、

$ϵ=\frac{\lambda }{L_0}$

となるテンプレート:Sfn。試料の形状に寄らずに材料の強度や変形の挙動を評価するために、荷重-変形曲線ではなく、応力-ひずみ曲線が用いられるテンプレート:Sfn。

応力とひずみの定義

引張を受ける丸棒の変形の様子。左図が荷重を受けていない初期状態を示す。

実際の引張試験片。真ん中の細い部分が伸びの測定に使われる。

テンプレート:See2 試料の断面積 A は荷重によって変動する。そのため応力-ひずみ曲線を得る場合、荷重をかけて変形する前の断面積を A₀ として、応力を

${\sigma }_n=\frac{F}{A_0}$

で定義する。このように定義した応力 σ_n を公称応力あるいは工学的応力と呼ぶテンプレート:Sfnテンプレート:Sfn。一方、変形中の断面積 A をもとに定義する応力を真応力と呼ぶテンプレート:Sfn。荷重 F が加わっているときの断面積を A とすれば、真応力 σ_t は以下のようになるテンプレート:Sfn。

${\sigma }_t=\frac{F}{A}$

この真応力は、応力の厳密な定義に近いテンプレート:Sfn。

試料の初期長さ L₀ で除して得られるひずみ ε_n は、公称ひずみや工学的ひずみと呼ばれるテンプレート:Sfnテンプレート:Sfn。

${ϵ}_n=\frac{\lambda }{L_0}$

公称ひずみに対して、荷重 F が加わった時点における長さ L からの変形量で定義するひずみを真ひずみと呼ぶテンプレート:Sfn。真ひずみ ε_t は微分形式で以下のように定義されるテンプレート:Sfn。

$d{ϵ}_t=\frac{dL}{L}$

ここで、dε と dL は、長さ L からのひずみ微小増加量と長さ微小増加量である。dε を L₀ から L まで積分すれば、以下のような真ひずみ ε_t と公称ひずみ ε_n の関係が得られるテンプレート:Sfn。

${ϵ}_t=\underset{L_0}{\overset{l}{\int }}\frac{dL}{L}=\ln \frac{L}{L_0}=\ln \frac{L_0+\lambda }{L_0}=\ln (1+{ϵ}_n)$

ここで、ln は自然対数である。真ひずみは対数ひずみとも呼ばれるテンプレート:Sfn。

真応力-真ひずみ曲線の方が物理的意味はあるが、その都度の断面積を測定する必要があるテンプレート:Sfn。公称応力-公称ひずみ曲線が慣例的によく使われるテンプレート:Sfn。

材料別の傾向

構造用鋼の応力-ひずみ曲線模式図
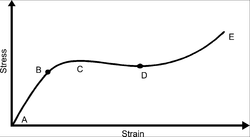
1と2の応力が、それぞれ引張強さと降伏点を示す。3に達したときに破断する。4の領域が均一塑性変形域、5.が不均一塑性変形域に該当する。Aが公称応力による曲線、Bが真応力による曲線

材料の種類によって応力-ひずみ曲線の特徴は異なる。以下では、金属材料、高分子材料、セラミックス材料について説明する。

金属材料

金属材料の中でも、材料の種類によって応力-ひずみ曲線の傾向が２種類に分かれるテンプレート:Sfn。以下では参照文献に倣い、特に断りが無い限り、引張荷重、室温、変位制御による公称応力-公称ひずみ曲線をもとに応力-ひずみ曲線の概要を説明する。

弾性変形領域

無負荷の状態から荷重をかけ始めると、ある程度の応力値まで、応力とひずみは比例の関係で結ばれるテンプレート:Sfn。このような比例の関係をフックの法則と呼び、フックの法則が保たれた変形を弾性変形と呼ぶテンプレート:Sfn。弾性変形領域内では、荷重を取り除くと変形はなくなり、元の形状に戻るテンプレート:Sfn。比例係数はヤング率と呼ばれ、次式の関係にあるテンプレート:Sfn。

${\sigma }_n=E{ϵ}_n$

ここで、E はヤング率で、σ_n、ε_n は公称応力と公称ひずみである。弾性変形領域内で強度設計することが、強度設計の基本となるテンプレート:Sfn。

ある程度までひずみが大きくなると材料が降伏し、比例関係が崩れて、応力とひずみの関係は非線形となる。この領域では除荷しても変形が完全には戻らなくなるテンプレート:Sfn。このような残留する変形を塑性変形と呼ぶテンプレート:Sfn。

均一塑性変形域

テンプレート:Double image stack

アルミニウムなど非鉄金属材料および炭素量の高い鉄鋼材料と、炭素量の少ない軟鋼とで、降伏の様子は異なってくるテンプレート:Sfnテンプレート:Sfn。非鉄金属の場合、線形（比例）から非線形へは連続的に変化するテンプレート:Sfn。比例ではなくなる限界の点を比例限度または比例限と呼び、比例限をもう少し過ぎた、応力を除いても変形が残る（塑性変形する）限界の点を弾性限度または弾性限と呼ぶテンプレート:Sfnテンプレート:Sfn。実際の測定では、比例限度と弾性限度は非常に近いので、それぞれを個別に特定するのは難しいテンプレート:Sfn。そのため、除荷後に残る永久ひずみが0.2%となる応力を耐力や0.2%耐力と呼び、比例限度や弾性限度の代わりに塑性変形発生基準として用いられるテンプレート:Sfnテンプレート:Sfn。

軟鋼の場合は、応力-ひずみ曲線の線形領域から非線形領域へは不連続的に変化する。応力が高くしていくと、ある点で塑性変形が開始する。この点を上降伏点と呼ぶテンプレート:Sfn。ここで、試料に対してを荷重制御ではなく変位制御で負荷を与えているとすると、強制的に与えられる伸びに追従して応力が発生する格好となる。変位制御で応力-ひずみ曲線を測定すると、上降伏点を過ぎた後、応力はあるところまで急激に下がり、ほぼ一定の応力状態が続くテンプレート:Sfnテンプレート:Sfn。下がったところの応力を下降伏点と呼ぶテンプレート:Sfn。下降伏点の応力値で一定の状態が続いた後、再度応力が増加していく。このような降伏の過程を辿るのは軟鋼特有の現象で、コットレル雰囲気などの理論で説明されるテンプレート:Sfn。上降伏点と下降伏点の総称を、あるいは下降伏点と上降伏点を区別しない場合は上降伏点を、降伏点と呼ぶテンプレート:Sfnテンプレート:Sfn。下降伏点における一定応力値が続く範囲のひずみを降伏点伸びと呼ぶテンプレート:Sfn。下降伏点と上降伏点を区別しない場合、降伏点における応力を、降伏応力、降伏強度、降伏強さ、あるいは単に降伏点と呼ぶテンプレート:Sfn。

降伏後、応力-ひずみ曲線は再び上昇していくテンプレート:Sfn。ここからは、塑性変形が起きている材料に対してさらに塑性変形をさせようとしており、このため応力の増加が必要となるテンプレート:Sfn。この現象は加工硬化やひずみ硬化と呼ばれ、金属中の転位の運動が妨げられるようになるため発生するテンプレート:Sfn。加工硬化後の真応力と真ひずみの関係は、

${\sigma }_t=K{ϵ}_t^n$

で表すことができる場合が多いテンプレート:Sfnテンプレート:Sfn。K は強度係数、n はひずみ硬化係数や加工硬化指数、n 値と呼ばれ、材料固有の定数となるテンプレート:Sfnテンプレート:Sfnテンプレート:Sfn。多くの金属で n は0.2から0.4までの値を取るテンプレート:Sfn。

降伏後の応力-ひずみ曲線を公称応力で追うと、加工硬化で上昇していった曲線は、あるひずみで応力が極大値をとる。降伏から公称応力極大までの変形は、試験片全体にわたって均一に塑性変形が発生するので、均一塑性変形とも呼ばれるテンプレート:Sfn。均一塑性変形中は、全断面積で応力は均一に分布しているテンプレート:Sfn。

不均一塑性変形域

破断に達した試験片の様子

降伏後の応力-ひずみ曲線を公称応力で追うと、あるひずみで応力が最大となり、そこからは応力は下がっていく。この最大応力を引張強さと呼ぶテンプレート:Sfn。引張強さは材料の強度を示す重要な特性値で、引張における強度の指標として最も広く使用されているテンプレート:Sfnテンプレート:Sfn。この最大応力を境にして材料の変形は、均一な変形ではなく、試験片の一部が局部的に縮小するようになるテンプレート:Sfn。したがって、ここからの局部縮小を伴う塑性変形を不均一塑性変形と呼ぶテンプレート:Sfn。発生する局部縮小をくびれ、またはネッキングと呼ぶテンプレート:Sfn。

さらに荷重をかけ続けると、発生したくびれは縮小し続け、そこから試験片の破断に至るテンプレート:Sfn。公称応力で見たとき、破断時の応力は引張強さよりも小さくなるが、真応力で見れば、加工硬化による真応力増大は続き、破断応力は引張強さよりも大きな値を示すテンプレート:Sfnテンプレート:Sfn。ただし、破断応力の値を用いることは一般的には少ないテンプレート:Sfn。破断時の公称応力を公称破断応力、あるいは単に破断応力と呼ぶテンプレート:Sfnテンプレート:Sfn。破断時の荷重を破断部の断面積で除した値、すなわち破断応力を真応力で表したものは真破断応力と呼ぶテンプレート:Sfn。

初期長さと破断後長さの変化率を破断伸びや単に伸びと呼ぶテンプレート:Sfnテンプレート:Sfn。初期長さを L₀、破断後長さを L_f とすれば、伸び δ は百分率 [%] で、

$\delta =\frac{L_f-L_0}{L_0}\times 100$

で表されるテンプレート:Sfn。破断伸びは材料の靱性を示す特性値となるテンプレート:Sfn。実際の試験では、破断して残った2つの試験片をきれいに突き合わせ、予め記しておいた標点間の距離で破断後長さを測定するテンプレート:Sfn。

また、破断後の断面積の減少率を絞りと呼ぶテンプレート:Sfn。伸びと同様に靱性を示す特性値の一つであるテンプレート:Sfn。破断部の断面積を A_f、初期断面積 A₀ とすると、絞り φ は伸びと同じく百分率で、

$\varphi =\frac{A_0-A_f}{A_0}\times 100$

で定義されるテンプレート:Sfn。

高分子材料

高分子材料の公称応力-公称ひずみ曲線の一例

高分子材料は、粘性弾性を示す材料で、金属材料と粘性流体の間のような力学的性質を示す。そのため、フックの法則に従う領域は、応力が低い範囲であってもほぼ無いか狭いテンプレート:Sfn。そのため高分子材料の場合は、原点付近での曲線の接線からヤング率を求めるテンプレート:Sfn。

高分子材料は種類が多様なため、応力-ひずみ曲線の形状も様々であるテンプレート:Sfn。金属のような曲線を持つものから、ゴムのように著しく伸びやすいものまで存在するテンプレート:Sfn。温度とひずみ速度の影響も受けやすく、高い温度または小さなひずみ速度では、応力-ひずみ曲線の背は低くく、破断ひずみは大きくなり、より延性的な材質になる。一方、低い温度または大きなひずみ速度では、応力-ひずみ曲線の背は高く、破断ひずみが小さくなり、より脆性的な材質になる。

セラミックス材料

セラミックスは典型的な脆性材料であるテンプレート:Sfn。一般に、セラミックスのヤング率は金属よりも高いテンプレート:Sfn。引張荷重をかけたとき、塑性変形をほとんど起こさずに破壊に至るテンプレート:Sfn。圧縮荷重の場合、塑性変形を起こさないのは同様だが、き裂が安定して成長するため、応力-ひずみ曲線の最大値である圧縮強さは引張強さの10倍から20倍となるテンプレート:Sfn。

参照文献

• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp

外部リンク

• テンプレート:機械工学事典
• テンプレート:Commonscat-inline