統計学

提供: testwiki
ナビゲーションに移動 検索に移動

テンプレート:出典の明記

正規分布は非常に一般的な確率密度関数の一つであり、中心極限定理により有用となっている。
散布図は、さまざまな変数間で観測された関係を示すために記述統計で利用される。この散布図はテンプレート:Illを使用している。

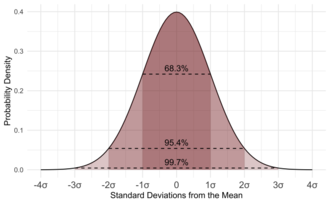
統計学（とうけいがく、テンプレート:Lang-en-short）とは、統計に関する研究を行う学問である。経験的に得られたバラツキのあるデータから、応用数学の手法を用いて数値上の性質や規則性あるいは不規則性を見いだす。統計的手法は、実験計画、データの要約や解釈を行う上での根拠を提供するため、幅広い分野で応用されているテンプレート:Efn。

物理学・経済学[1][2]・社会学・心理学[3]・言語学といった人文科学・社会科学・自然科学（基礎科学）から、工学・医学[4]・薬学といった応用科学まで、実証分析を伴う科学の分野において必須の学問となっている。また、科学哲学における重要なトピックの一つでもある。

語源

テンプレート:Main 英語で統計または統計学を「テンプレート:読み仮名」と言うが、語源はラテン語で「状態」を意味する「テンプレート:読み仮名」であり、この言葉がイタリア語で「国家」を意味するようになり、国家の人力、財力等といった国勢調査を比較検討する学問を意味するようになったテンプレート:要出典[注釈 1]。

なお、統計学という語は、ドイツの政治学者ゴットフリート・アッヘンヴァルが1749年に『ヨーロッパ諸国国家学綱要』の中で、それまでドイツ語で「Staatenkunde」（「国情論」の意味）と呼ばれていたテンプレート:Sfn学問に「テンプレート:読み仮名」（統計学）の名をつけたことに始まるテンプレート:Sfn。

日本語の「統計」という語の起源は明確にはなっていないが、幕末から明治初年にかけての洋学者である柳川春三が初めて現在の意味でこの語を使用したと考えられており、明治2年（1869年）には彼の編纂した冊子においてこの語と用法が使用されたとの記述がある。その後、明治4年（1871年）には大蔵省に「統計司」（後に「統計寮」に改組）が置かれ、次第にこの語が広まっていった[5]。

分類

記述統計学と推計統計学

テンプレート:Main 統計学は「記述統計学 (descriptive statistics) 」 と「推計統計学（inferential statistics、推測統計学とも） 」に分類できる[6]。記述統計学はデータの特徴を記述する学問であり、推計統計学は標本から母集団を推計する学問である。

記述統計学は、データ1つがもつ特徴を記述・説明することに着目した分野である[6]。例えば小学生99人の身長データがあったとする。データの値は個別の小学生のものであり、100人全体の特徴は値を個別に見ただけでは分からない。ここでデータの値を身長順に並べ、50番目の値を見れば「この小学生99人の"普通"の身長はだいたい110 cmである」と記述できる。50番目の値は中央値という。このように、データ全体の特徴を要約・記述することが記述統計学の大きな目的・方法論である。

推計統計学は、母集団からの標本化を前提とし、標本から母集団を推測する分野である[6]。例えば世界の小学生の身長特性を知りたいとする。全世界の小学生の身長を計測し記述統計学によって中央値や平均値を記述すれば、目的である世界の小学生の身長特性は解明できる。しかしその計測は著しく困難（事実上不可能）である。そこで推計統計学では、まず小学生100人の身長データ（標本と呼ぶ）を集める。そして標本は全世界の小学生という母集団からランダムに選ばれたものだと考える。ランダムに選ばれた100人の身長中央値（標本の中央値）は必ずしも世界小学生身長中央値（母集団の中央値）と一致しないと考えられるが、"似た"数値にはなると期待される。すなわち標本から母集団の特性を推測することができる。この、標本から母集団を推測する方法論に関する分野が推計統計学である。

このように、記述統計学はデータ（推計統計学でいう標本）の説明・記述を行い、推計統計学は母集団（の記述）の推測をおこなう。両分野の違いは、記述統計学では目の前にあるデータがすべて（母集団という考え方はない）のに対し、推計統計学ではむしろ目の前のデータは（真なる）母集団から今回たまたま選ばれた標本だと考える点にある。一方で、推計統計学では標本の記述統計から母集団の統計量を推測するように、この2分野は非常に密接に絡んでおり全く別の分野と考えることは不適切である。

統計的手法

テンプレート:出典の明記

実験計画法
データ収集の規模や対象、割付方法をコントロールし、より公正で評価可能なデータが収集できるよう検討すること。統計の世界には「ゴミのようなデータを使っていくら解析しても出てくる結果はゴミばかりだ」[7]という格言があるテンプレート:Sfn。これはデータ収集の前にその方法を十分に検討する必要があることを強調したものである。
尺度水準
データ（あるいは変数、測定）の尺度はふつう次のような種類（水準）に分類される。尺度水準によって、統計に用いるべき要約統計量や統計検定法が異なる。
  • 質的データ、カテゴリデータ
    • 名義尺度：単なる番号で順番の意味はない。電話番号、背番号など。
    • 順序尺度：順序が意味を持つ番号。階級や階層など。
  • 量的データ、数値データ
    • 間隔尺度：順序に加え間隔にも意味がある（単位がある）が、ゼロには絶対的な意味はない。摂氏・華氏、知能指数など。
    • 比率尺度：ゼロを基準とする絶対的尺度で、間隔だけでなく比率にも意味がある。絶対温度、金額など。

これらは、意思決定に応用されている。

歴史

テンプレート:Main 統計学の源流は国家または社会全体における人口あるいは経済に関する調査にあるテンプレート:Sfn。このことは、東西を問わず古代から行われている。

学問としては、17世紀にはイギリスでウィリアム・ペティの『政治算術』（1790年）などが著述され、その後の社会統計学に繋がる流れが始まった。彼の提唱した政治算術そのものは18世紀に衰退するものの、ペティは統計学の父とも呼ばれるテンプレート:Sfn。また同時期、ペティの友人であるテンプレート:日本語版にない記事リンクが『死亡表に関する自然的および政治的諸観察』（1662年）を表し、人口統計学の源流となったテンプレート:Sfn。この死亡統計の研究はエドモンド・ハレーなども行うようになったテンプレート:Sfn。これらの影響の基、18世紀にはドイツのヨハン・ペーター・ジュースミルヒが『神の秩序』（1741年）で人口動態にみられる規則性を明らかにしたが、これには文字通り「神の秩序」を数学的に記述する意図があったテンプレート:Sfn。

ドイツでは17世紀からヘルマン・コンリングなどによってヨーロッパ各国の国状の比較研究が盛んになり、1749年にゴットフリート・アッヘンヴァルがこれにドイツ語で「テンプレート:読み仮名」（「統計学」の意味）の名をつけているテンプレート:Sfn。

19世紀初頭になるとこれに関して政治算術的なデータの収集と分析が重視されて、「テンプレート:Lang」の語は特に「統計学」の意味に用いられ、さらにイギリスやフランスなどでも用いられるようになった。この頃には、1748年のスウェーデンを皮切りに国勢調査も行われるようになり、1790年には下院の議員数算定のためにアメリカがこれに続き、イギリス、フランスなど西ヨーロッパ諸国においても1830年頃までには国勢調査が行われるようになったテンプレート:Sfn。

一方ブレーズ・パスカル、ピエール・ド・フェルマーに始まった確率論の研究がフランスを中心にして進み、19世紀初頭にはピエール＝シモン・ラプラスによって一応の完成を見ていたテンプレート:Sfn。また、カール・フリードリヒ・ガウスによる誤差や正規分布についての研究も統計学発展の基礎となったテンプレート:Sfn。ラプラスも確率論の社会的な応用を考えたが、この考えを本格的に広めたのが「近代統計学の父」と呼ばれるアドルフ・ケトレーであった。彼は『人間について』（1835年）、『社会物理学』（1869年）などを著し、自由意志によってばらばらに動くように見える人間の行動も社会全体で平均すれば法則に従っている（「平均人」を中心に正規分布に従う）と考えたテンプレート:Sfn。ケトレーの仕事を契機として、19世紀半ば以降、社会統計学がドイツを中心に、特に経済学と密接な関係を持って発展する。代表的な人物にはアドルフ・ワグナーテンプレート:Sfn、エルンスト・エンゲル（エンゲル係数で有名）テンプレート:Sfn、ゲオルク・フォン・マイヤーがいるテンプレート:Sfn。またフローレンス・ナイチンゲールも、社会医学に統計学を応用した最初期の人物として知られる。統計学の業績について高く評価され1858年には王立統計学会初の女性会員となった[8]。

同じく19世紀半ばにチャールズ・ダーウィンの進化論が発表され、彼の従弟に当たるフランシス・ゴルトンは数量的側面から生物進化の研究に着手した。これは当時「テンプレート:読み仮名」（生物測定学）と呼ばれ、多数の生物（ヒトも含めて）を対象として扱う統計学的側面を含んでいる[9]。ゴルトンは平均への回帰の発見で有名であるテンプレート:Sfnが、当初生物学的と思われたこの現象は一般の統計学的対象の解析でも重要であることが明らかとなる。ゴルトンの後継者となった数学者カール・ピアソンはこのような生物統計学をさらに数学的に発展させ（数理統計学）、19世紀終わりから20世紀にかけ記述統計学を大成するテンプレート:Sfn[注釈 2]。

20世紀に入ると、ウィリアム・ゴセットテンプレート:Sfn、続いてロナルド・フィッシャーが農学の実験計画法研究をきっかけとして数々の統計学的仮説検定法を編み出し、記述統計学から推計統計学の時代に移るテンプレート:Sfn。ここでは母集団から抽出された標本を基に、確率論を利用して逆に母集団を推定するという考え方がとられる。続いてイェジ・ネイマン、エゴン・ピアソンらによって無作為抽出法の採用など現代の数理統計学の理論体系が構築されテンプレート:Sfn、これは社会科学、医学、工学、オペレーションズ・リサーチなどの様々な分野へ応用されることとなった。

こうして推計統計学は精緻な数学理論となった反面、応用には必ずしも適していないとの批判が常にあった。

これに呼応して、在来の客観確率を前提に置く統計学に対し、それまでごく少数によって提唱されていたにすぎなかった主観確率を中心に据えたベイズ統計学が1954年にテンプレート:仮リンクの『統計学の基礎』によって復活したテンプレート:Sfn。ベイズの定理に依拠する主観確率の考え方は母集団の前提を必要とせず不完全情報環境下での計算や原因の確率を語るなど、およそ在来統計学とは正反対の立場に立つため、その当時在来統計学派はベイズ統計学派のことを『ベイジアン』と名付けて激しく対立した。しかし主観確率には、新たに取得した情報によって確率を更新する機能（＝ベイズ推定）が内包され、この点が大きな応用の道を開いた。今や統計学では世界的にベイズ統計学が主流となり、先端的応用分野ではもっぱらベイズ統計学が駆使されている。

計量経済学、統計力学[10][11][12]、バイオテクノロジー、疫学、機械学習、データマイニング、制御理論、インターネットなど、あらゆる分野でベイズ統計学は実学として活用されている。スパムメールフィルタや日本語入力システムの入力予測など身近な応用も数多い。20世紀末にはマルコフ連鎖モンテカルロ法など理論面で様々な革新的考案もなされ、旧来の統計学では不可能であったような各分野で多くの応用がなされるようになっている。これらベイズ統計学についての展開は、いずれも計算環境の進歩と不可分であるテンプレート:Sfn。

他分野との関係

確率論

確率論は、中等教育で「確率・統計」と一括りに呼ばれていたように[13][14]、統計学と非常に深いかかわりがある[15][16][17][18][19][20][21]。推計統計学ではデータ（標本）が母集団からランダムに取り出されるという前提に立っている。すなわち母集団を構成する要素はそれぞれ"出やすさ"をもっており、それに従ってランダムに取り出されるという立場である。"出やすさ"はまさしく（古典的な）確率であり、母集団はある確率分布に従っていると数学的に表現できる。標本に基づいた母集団確率分布のパラメータ推定（統計的推論）は推計統計学の花形であり、これらは確率論の用語や理論を用いて表現・研究されている。

x∼ptrue(x|θ): 標本 x は、パラメータ θ をもつ確率分布 pテンプレート:Sub に従う母集団からサンプリングされる。

機械学習

機械学習では、機械（数理モデル）がデータを利用してその性能を向上させようとする[22][23][24]。数理モデルとして確率分布を含むモデルを考えた場合、このモデルがデータを生成する過程は、まさしく推測統計学における母集団からのサンプリング（確率分布で表現された母集団モデルからデータという標本を取り出す過程）といえる。そしてこのモデルの学習とは、データからの正確な確率モデル推定 = 標本からの母集団パラメータ推定であり、すなわち統計的推論と同義である。このように統計学と機械学習には深い関係がある[25]（詳しくは テンプレート:節リンク）

再現性の危機

テンプレート:Main 一度信頼できる統計データが取れさえすれば統計学的分析は数学的に行えるが、信頼できる統計データの収集はとても難しい。統計学の源流は各国が人口その他を把握するために行った国勢調査に求められるが、古代・中世を通じほとんどの国家では中央権力の力が弱く、ローマ帝国で行われたセンサステンプレート:Sfnや中国歴代王朝の人口調査テンプレート:Sfn等の例外はあるものの、特に大国においてこうした調査を行うことはほぼ不可能だった。

こうした調査が実行可能となるのは各国の中央政府の行政能力の向上した18世紀から19世紀初頭にかけてであり、この時期に初めて近代的な意味での統計学が成立することとなったテンプレート:Sfn。現代においても、たとえば行政能力の脆弱なブラックアフリカ諸国においては統計局の予算・人員の不足が深刻であり、統計データの不正確さが指摘されているテンプレート:Sfn。

また、統計を取る人の主義主張によって統計値が大きく異なることも多々あり、ロナルド・レーガン政権は当時アメリカにホームレスが30万人しかいないと主張したが、活動家たちはその10倍の300万人いると主張したテンプレート:Sfn。

例えば、質問の仕方一つで結果がガラリと変わってしまう。強姦に関するある調査で、女子大生に「男性からアルコールや薬物を飲まされて、望まない性交をしたことがありますか」と質問することで「女子大生の1/4が強姦されたことがある」という結論を出したが、批判者たちはこの調査で強姦体験者と認定された女子大生たちを集めて再調査したところ、その3/4がその体験を強姦だと考えていないことが分かったテンプレート:Sfn。

また、暗数の考慮にも主観がつきまとってしまう。暗数とは「統計に出ない値」のことで、例えば強姦のような犯罪はそれがタブーであるために警察に届けないことも多く、したがって統計に表れない。それには統計を正しく読み解くには暗数を考慮する必要があるが、統計値を多く見積もりたい人は意識的・無意識的に暗数を多く見積もってしまう可能性があり、逆に統計値を少なく見積もりたい人は暗数を少なく見積もってしまう可能性がある。

正しい統計データから正しい統計操作を行ってもなお騙すことが可能である。たとえば、ここ四十数年で少年犯罪は1/4になっているが、最近10年では微増している。この時、微増となっている最近10年分のデータだけを提示して、「近年少年犯罪は増加している」という主張をすれば、これは成立することになる[26]。さらに、グラフの縦軸（=犯罪数の軸）をわざと縦長に描くことで犯罪数が急上昇しているかのように見せかけることも可能である。

反証可能性

カール・ポパーの反証可能性理論が、反証可能性のない理論は非科学的であると主張したため、反証可能性のない統計理論が存在する場合、それは非科学的であるとする論文があることに留意すべきである[27]。

教育

統計学は「実学」に端を発しており、市民社会以降世界に普及した「市場経済」を牽引した原動力とも言える学問である。そのため、自然科学・社会科学・人文科学の各分野の垣根を越えて分化かつ拡大を続ける中、基礎において汎用性が高い学問の構造を有しているテンプレート:要出典。

社会生活の至る所で統計技術の適用が貢献できる場面がある以上、統計学とその適用方法を学習する上では社会の実態に即して頻繁に技法を適用してみることが重要であり、そのように出来るためには何よりまず統計処理を身近で制限無く実施できるような「統計処理環境」の備えが必要である。

PC・ソフトウェア・インターネットなどのIT環境が急速に進化低廉化して普及したことで身近に統計処理環境を持ちうるようになり、なおかつ莫大な統計情報がインターネットを通じて公開されているため、研究・調査・学習の処理材料にも不自由しない。

実際21世紀に入って以降は、それまでの確率論と数理統計学を重点に置いたカリキュラムに加え、データを処理して求める答えに近づく「データ解析」のスキルが教育されるようになっている（データサイエンス論）。

元来コンピュータを使った数値解析に際してはまず、IEEE 754規格にあるように端数処理誤差が暗黙のうちに生じることや、有効数字の概念の認識が重要で、子供のころ算数で学んだような計算結果にはならないことがあることを知っておかねばならない。さらに、統計計算では殊に重要な乱数列についても、コンピュータ上で用いるのは擬似乱数であることや、良質な疑似乱数生成方式「メルセンヌ・ツイスタ」を計算ソフトウェアや開発用言語の全てが必ず備えているわけではないこと、暗号論的乱数はさらにまた別の乱数概念であること、なども実は大切な基礎知識である。

人が得意とするパターン認識の力を積極的に用いるため、統計データの「グラフ化」が古来常套手段として用いられているが、ITの支援を得ることで大量のデータを様々な形に、しかも瞬時にグラフ化（あるいは『可視化』）することが可能となった。そのためのグラフ作成ソフトも多数存在するが、その他の数値解析ソフトウェアや数式処理システム、そして殊に下記のような統計アプリケーションではグラフ化するための機能が充実している。

一方、近年オフィスソフト機能等で極端なグラフ装飾を施すことが横行している。この結果として、例えば3Dグラフなどを安易に用いると遠近感や区間面積などから表示すべき真の数量とは異なった認識を受け手に与える事がある。本来3Dグラフ表示は人の空間認識力を活かし得る優れた表現手法であるが、意味なく勢い付け等で用いるのは本来的な視覚化からは退行するばかりか、意図して受け手の誤認識を誘導する事も可能となる。「グラフは直感的に分かるから全て善である」と一般に認識されていることや、前出「統計の困難さ」にある内容をふまえると、統計の視覚化とその解釈に関するリテラシ教育は初等段階から特に注意を要する。

上記のように、用いる統計処理環境ごとに適用分野・目的・方法論・使用者との相性などは異なる。そういった統計処理環境固有の特性なども含めて、いかなる道具もそうであるように、数多く体験の機会を作るほかに理解の早道は無い。

広く普及した表計算ソフトが統計処理・グラフ表現機能を持っているので、誰でも手軽に統計処理入門体験は出来る。しかしあくまでビジネスソフトであり、科学技術ソフトではないExcelの計算の信頼性については常に批判が絶えない[28][29][30][31]（Excelに限らず普及している表計算ソフトウェアはどれも信頼に足る統計計算はできないとの報告もある[32]）。

近年では研究・教育機関が公開するオープンソースな自由ソフトウェアの中からきわめて優秀な計算ソフトウェアが育っており、プロプライエタリソフトの問題点顕在化により関心の高まった統計技術資産の持続可能性という観点からも、統計教育にあたってはこれらオープンソースソフトウェアの積極的な活用が推奨される。

統計の研究・教育に適した代表的なフリーソフトウェア テンプレート:Div col

テンプレート:Div col end 統計計算に関連するソフトウェアのカテゴリ

日本

日本においては統計学がそれぞれの分野へ分化された形で組み込まれているため「統計学科」を置く大学がなかったが、2017年度に滋賀大学が日本で初めて統計学を研究の核とするデータサイエンス学部を新設。一橋大学がソーシャル・データサイエンス研究科・学部を2023年度に新設予定である。

国立の統計学研究・教育機関としては、1944年に設立された統計数理研究所があり、AIC、数量化理論、確率微分方程式などの顕著な成果を生み出し、統計学研究を牽引している[注釈 3]。

平成21年（2009年）11月に公示された[45]新学習指導要領において、中学・高校数学における統計単元の拡充がなされた。

中学校では、中学数学においては「統計」を扱う単元が新設された（従来は確率を扱う単元はあったが統計処理を扱う単元はなかった）。

高校では、それまで高校数学Bにおいて選択履修とされていた「統計の基礎的概念」（代表値・相関係数ほか）を扱う単元が数学Iに移され「データの分析」として必修化された。また、それまで数学Cにおいて理系生のみが履修していた「確率分布と統計的な推測」が数学Bに移されて、文系生でも履修可能になった。

これらの変更は2012年（平成24年）度入学生から適用されている。（詳細は、「 数学 (教科) 」を参照）

「データの分析」はデータの散らばりと相関について教え、その目的は「統計の基本的な考えを理解するとともに，それを用いてデータを整理・分析し傾向を把握できるようにする。」ことである。総務省統計局では「学校における統計教育の位置づけ」[46][47]を解説し、指導者の支援にあたっている。

統計学の用語

テンプレート:Div col

テンプレート:Div col end

脚注

テンプレート:脚注ヘルプ

注釈

テンプレート:Notelist

出典

テンプレート:Reflist

参考文献

教科書など

（今後拡充する）

  • 宮川雅巳：「統計的因果推論：回帰分析の新しい枠組み」、朝倉書店（シリーズ 予測と発見の科学 1）、ISBN 978-4-254-12781-2 (2004年3月25日).
  • 小西貞則、北川源四郎：「情報量規準」、朝倉書店（シリーズ 予測と発見の科学 2）、ISBN 978-4-254-12782-9 (2004年9月25日).
  • 小西貞則、越智義道、大森裕浩：「計算統計学の方法：ブートストラップ、EMアルゴリズム、MCMC」、朝倉書店（シリーズ 予測と発見の科学　5）、ISBN 978-4-254-12785-0 (2008年3月25日).
  • 小西貞則：「多変量解析入門：線形から非線形へ」、岩波書店、ISBN 978-4-00-005653-3 (2010年1月26日).
  • 久保川達也：「データ解析のための数理統計入門」、共立出版、ISBN 978-4-320-11551--4 (2023年10月15日).

関連項目

テンプレート:Div col

テンプレート:Div col end

外部リンク

テンプレート:Wikibooks テンプレート:Commonscat テンプレート:Wiktionary

テンプレート:Statistics-stub テンプレート:統計学 テンプレート:Authority control

  1. ↑ Wonnacott, T. H., & Wonnacott, R. J. (1990). Introductory statistics for business and economics (Vol. 4). New York: Wiley.
  2. ↑ Newbold, P., Carlson, W. L., & Thorne, B. (2013). Statistics for business and economics. Boston, MA: Pearson.
  3. ↑ Aron, A., & Aron, E. N. (1999). Statistics for psychology. Prentice-Hall, Inc.
  4. ↑ Lang, T. A., Lang, T., & Secic, M. (2006). How to report statistics in medicine: annotated guidelines for authors, editors, and reviewers. ACP Press.
  5. ↑ 「統計」という言葉の起源（2022年10月22日閲覧）
  6. ↑ 6.0 6.1 6.2 テンプレート:Wayback
  7. ↑ テンプレート:Lang-en-short
  8. ↑ 「人間と社会を変えた9つの確率・統計学物語」p.162 松原望 SBクリエイティブ 2015年4月24日初版発行
  9. ↑ 「生体認証国家 グローバルな監視政治と南アフリカの近現代」ｐ.32 キース・ブレッケンリッジ 堀内隆行訳 2017年8月24日第1刷 岩波書店
  10. ↑ Tolman, R. C. (1979). The principles of statistical mechanics. Courier Corporation.
  11. ↑ Ruelle, D. (1999). Statistical mechanics: Rigorous results. World Scientific.
  12. ↑ Thompson, C. J. (2015). Mathematical statistical mechanics. Princeton University Press.
  13. ↑ 第３節　数　　学 < 高等学校学習指導要領（昭和57年４月施行）
  14. ↑ 詳しくは「確率・統計」も参照のこと。
  15. ↑ Chow, Y. S., & Teicher, H. (2003). Probability theory: independence, interchangeability, martingales. Springer Science & Business Media.
  16. ↑ Feller, W. (2008). An introduction to probability theory and its applications (Vol. 2). John Wiley & Sons.
  17. ↑ Durrett, R. (2019). Probability: theory and examples (Vol. 49). Cambridge University Press.
  18. ↑ Jaynes, E. T. (2003). Probability theory: The logic of science. Cambridge University Press.
  19. ↑ Chung, K. L., & Zhong, K. (2001). A course in probability theory. Academic Press.
  20. ↑ 赤摂也. (2014). 確率論入門. 筑摩書房.
  21. ↑ 池田信行, 小倉幸雄, 高橋陽一郎, & 眞鍋昭治郎共著. (2006). 確率論入門.
  22. ↑ Alpaydin, E. (2020). Introduction to machine learning. MIT Press.
  23. ↑ Marsland, S. (2015). Machine learning: an algorithmic perspective. CRC Press.
  24. ↑ 大関真之. (2016). 機械学習入門 ボルツマン機械学習から深層学習まで. 株式会社 オーム社.
  25. ↑ Murphy, K. P. (2012). Machine learning: a probabilistic perspective. MIT Press.
  26. ↑ テンプレート:Cite book
  27. ↑ テンプレート:Cite journal
  28. ↑ Excel使うな Okumura's Blog 三重大学高等教育創造開発センター教授・教育情報システム部門長 奥村晴彦のブログ
  29. ↑ テンプレート:Cite journal
  30. ↑ Excel は，コンピュータ・ソフトウェアの三種の神器のようになっていますが，とんでもないこともあるというお話。 群馬大学社会情報学部教授 青木繁伸のサイト
  31. ↑ 間違いだらけのExcel関数ヘルプ「財務・統計関数編」市販解説本で孫引きしている点も警告
  32. ↑ On the Numerical Accuracy of Spreadsheets : the Journal of Statistical Software Vol.34, Issue4, Apr2010
  33. ↑ Ihaka, R., & Gentleman, R. (1996). R: a language for data analysis and graphics. Journal of computational and graphical statistics, 5(3), 299-314.
  34. ↑ Octaveの精義 - フリーの高機能数値計算ツールを使いこなす, 松田七美男(2011)
  35. ↑ Bunks, C., Chancelier, J. P., Delebecque, F., Goursat, M., Nikoukhah, R., & Steer, S. (2012). Engineering and scientific computing with Scilab. Springer Science & Business Media.
  36. ↑ 大野修一. (2009). Scilab 入門: フリーソフトで始める数値シミュレーション. CQ出版.
  37. ↑ 上坂吉則. (2010). Scilab プログラミング入門. 牧野書店.
  38. ↑ Thanki, R. M., & Kothari, A. M. (2019). Digital image processing using SCILAB. Springer International Publishing.
  39. ↑ 岩城秀樹：「Maximaで学ぶ経済・ファイナンス基礎数学」、共立出版、ISBN 978-4320110311（2012年12月8日）
  40. ↑ Noro, M., & Takeshima, T. (1992, August). Risa/Asir-a computer algebra system. In Papers from the international symposium on Symbolic and algebraic computation (pp. 387-396).
  41. ↑ Noro, M. (2003). A computer algebra system: Risa/Asir. In Algebra, Geometry and Software Systems (pp. 147-162). Springer, Berlin, Heidelberg.
  42. ↑ Jones, E., Oliphant, T., & Peterson, P. (2001). SciPy: Open source scientific tools for Python.
  43. ↑ Bressert, E. (2012). SciPy and NumPy: an overview for developers. " O'Reilly Media, Inc.".
  44. ↑ Blanco-Silva, F. J. (2013). Learning SciPy for numerical and scientific computing. Packt Publishing Ltd.
  45. ↑ 高等学校学習指導要領解説・数学編 - 文部科学省
  46. ↑ 学校における統計教育の位置づけ｜統計学習の指導のために（先生向け）
  47. ↑ 学校における統計教育の位置づけ < 統計学習の指導のために 先生向け < 統計局ホームページ
  48. ↑ 渡部洋. (1999). ベイズ統計学入門. 福村出版.
  49. ↑ 中妻照雄. (2007). 入門ベイズ統計学.
  50. ↑ 豊田秀樹. (2015). 基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門. Asakura Shoten.
  51. ↑ 松原望. (2010). ベイズ統計学概説: フィッシャーからベイズへ. 培風館.
  52. ↑ 樋口知之. (2011). 予測にいかす統計モデリングの基本―ベイズ統計入門から応用まで. 講談社.


引用エラー: 「注釈」という名前のグループの <ref> タグがありますが、対応する <references group="注釈"/> タグが見つかりません

「https://ja.wiki.beta.math.wmflabs.org/w/index.php?title=統計学&oldid=16」から取得