同値関係

テンプレート:About テンプレート:出典の明記数学において、同値関係（どうちかんけい、テンプレート:Lang-en-short）とは二項関係であって反射的、対称的、推移的の3つの性質を満たすものをいう。そのことから、与えられた集合上の1つの同値関係はその集合を同値類に分割（類別）することが導かれる。

同値関係にあることを表すのに用いられる記法は文献によってさまざまであるが、与えられた集合上の同値関係テンプレート:Mvar に関して2つの元テンプレート:Math2 が同値であることを "テンプレート:Math2" や "テンプレート:Math2" で表すことが最もよく用いられる。テンプレート:Mvar に関して同値であることを明示する場合には、"テンプレート:Math2" や "テンプレート:Math2" あるいは "テンプレート:Mvar" などと書かれる。

定義

ある集合テンプレート:Mvar において、以下の3つの性質をすべて満たす二項関係 $\sim$ はテンプレート:Mvar 上の同値関係であるという。それらの性質とはテンプレート:Mvar の任意の元テンプレート:Math2 に対して、

反射律： $a \sim a$ .
対称律： $a \sim b$ ならば $b \sim a$ .
推移律： $a \sim b$ かつ $b \sim c$ ならば $a \sim c$ .

上の3つをまとめて同値律ということがよくあるテンプレート:Sfn。 $\sim$ が同値関係であるときに、 $a \sim b$ であることを、テンプレート:Mvar とテンプレート:Mvar は同値であるというテンプレート:Sfn。

同値関係の例

相等関係 (テンプレート:Math)：集合としてあるいは集合の元として同じである。表現形式や構成要素が同一である。
図形の合同関係：位置や裏表や向きの違いを無視して、図形として同じである。
図形の相似関係：裏表・向き・大きさの比率の違いを無視して、図形の "形" としては同じである。
直線の平行関係：アフィン平面内の直線が交わらないか、一致する（傾きが同じである）。
量の比例関係：増え方・減り方の割合としては同じである。
整数の合同関係：ある数で割った余りが同じである。

以下のものは一般には、類における "関係" となる。

集合の濃度の対等 "関係"：集合の中身は別として、集合の大きさとしては同じである。
命題が同値であるという "関係"：2つの命題において、真偽（真理値）が同じである、または互いに片方から他方を証明できる。

諸概念

同値類

[a] : = {x \in S ∣ a \sim x} .

また、1つの同値類テンプレート:Mvar に対して、テンプレート:Math2 となるテンプレート:Mvar の元テンプレート:Mvar を1つ定めることを、テンプレート:Mvar の代表元としてテンプレート:Mvar をとるという。1つの同値類は、それに含まれている元を任意に選んでそれを代表元とする同値類を作ってもそれはもとと同じ同値類になる（同値類は代表元の取替えによって不変である）：

X = [x], y \in X ⟺ y \in [x] ⟺ x \sim y ⟺ x \in [y] ⟺ [y] = X, x \in X .

ゆえに同値類に関する性質を代表元の性質のみによって記述することは、一般には適当ではない。テンプレート:Mvar 上の同値関係テンプレート:Math が与えられたとき、テンプレート:Mvar の元に関する性質テンプレート:Mvar がテンプレート:Math2 なるとき常にテンプレート:Math ならばテンプレート:Math を満たすならば、性質テンプレート:Mvar は同値関係テンプレート:Math の下で well-defined であるとか、各同値類上で不変 (class invariant; 類不変) であるなどという。

そのようなものとしてよくあるのが、写像テンプレート:Math2 で、テンプレート:Math2 ならばテンプレート:Math2 なるときである。この場合、テンプレート:Mvar は各同値類上で定数 (class invariant under テンプレート:Math)、あるいはテンプレート:Math の下で不変 (invariant under テンプレート:Math), より短くテンプレート:Math-不変などという。このようなものは例えば有限群の指標論などで見かけることができる。また、このような写像の性質を可換三角図式として書き表すことができる（不変量なども参照）。文献によっては、不変という代わりに、テンプレート:Math に関する準同型 (morphism; 射) であるとかテンプレート:Math と両立する (compatible with テンプレート:Math) とか適合する ("respects テンプレート:Math") などのように言うこともある。

より一般に、（ある関係テンプレート:Math に関して）同値なものを（別の関係テンプレート:Math に関して）同値なものへ写す写像を考えることができて、そのような写像をテンプレート:Math からテンプレート:Math への準同型（あるいは射）などと呼ぶ。

商集合

集合テンプレート:Mvar の同値関係 $\sim$ から定まる同値類すべてを集めた集合のことを、集合テンプレート:Mvar を同値関係 $\sim$ で割った集合、あるいはテンプレート:Mvar の $\sim$ による商集合であるといい、

S / \sim : = {[x] ∣ x \in S}

と表す。集合テンプレート:Mvar の元に対してそれが属する同値類を対応させることにより、テンプレート:Mvarから商集合への自然な全射

π : S ↠ S / \sim; x \mapsto [x]

が与えられる。これを同値関係 $\sim$ に付随する商写像や標準射影という。

定理 (標準射影の普遍性)^[1]: 写像テンプレート:Math2 がテンプレート:Math2 ならばテンプレート:Math2 を満たすならば、商集合からの写像テンプレート:Math2 で $f = g \circ π$ （テンプレート:Mvar は標準射影）を満たすものが一意に存在する。さらに、テンプレート:Mvar が全射かつテンプレート:Math2 を満たすとき、テンプレート:Mvar は全単射となる。

また、テンプレート:Mvar の相異なるすべての同値類から代表元を1つずつ集めて作ったテンプレート:Mvar の部分集合のことを、集合テンプレート:Mvar における同値関係 $\sim$ の（あるいは商集合 $S / \sim$ の）完全代表系 (テンプレート:En) と呼ぶ。つまり、集合テンプレート:Mvar の部分集合テンプレート:Mvar が同値関係 $\sim$ についての完全代表系であるとは、包含写像と標準射影の合成 $A ↪ S ↠ S / \sim; a \mapsto [a]$ が全単射となることである。

類別

定理 (同値関係と類別の関係)

集合テンプレート:Mvar 上の同値関係テンプレート:Math はテンプレート:Mvar を類別する。
テンプレート:Mvar の任意の類別に対してテンプレート:Mvar 上の同値関係テンプレート:Math が一意的に対応する。

これが同値関係と類別の間の基本的な結果である^[2]^[3]^[4]。いずれの主張も、テンプレート:Mvar の分割のセル全体のなす集合がテンプレート:Mvar のテンプレート:Math に関する同値類全体のなす集合に一致する。テンプレート:Mvar の各元テンプレート:Mvar はテンプレート:Mvar の分割のセルのうちただ1つのみに属するのであるから（かつ、各セルは同値類と同一視できるのだから）、各元テンプレート:Mvar はテンプレート:Mvar の同値類のうちただ1つのみに属する。従って、テンプレート:Mvar 上で可能な同値関係全体のなす集合とテンプレート:Mvar の分割全体のなす集合との間には自然な全単射が存在することがわかる。

同値核

テンプレート:See also 写像テンプレート:Mvar の同値核 (equivalence kernel) あるいはテンプレート:Mvar に付随する同値関係テンプレート:Sfnとは、

x \sim y ⟺ f (x) = f (y)

で定義される関係テンプレート:Math を言う。

同値関係の比較

テンプレート:Seealso 集合テンプレート:Mvar 上の2つの同値関係テンプレート:Math がテンプレート:Math2 ならばテンプレート:Math2 を任意のテンプレート:Math2 に対して満たすとき、同値関係テンプレート:Math はテンプレート:Math より粗い (coarser) または弱いといい、テンプレート:Math はテンプレート:Math より細かい (finer) または強いという。

同値類の言葉で言えば

テンプレート:Math がテンプレート:Math より細かい（強い）とは、テンプレート:Math に関する任意の同値類がテンプレート:Math に関する適当な同値類の部分集合となるときにいう。

それゆえ、テンプレート:Math に関する任意の同値類はテンプレート:Math に関する同値類の合併になる。すなわち

テンプレート:Math がテンプレート:Math より細かい（強い）とは、テンプレート:Math の定める分割がテンプレート:Math の定める分割の細分となるときに言う。

とも言い換えられる。

相等関係は任意の集合上で最も強い同値関係であり、自明な関係^[5]は最も弱い同値関係であり、任意の2つの元は互いに同値になる。

集合テンプレート:Mvar を固定して考えるとき、その上の同値関係全体の成す集合上で、"テンプレート:Math はテンプレート:Math より細かい" という関係はそれ自身半順序を成し、それによりテンプレート:Mvar 上の同値関係の全体はテンプレート:仮リンクをなす^[6]。

商集合の例

テンプレート:See also 整数全体のなす集合テンプレート:Mathbf に、テンプレート:Mvar とテンプレート:Mvar の差テンプレート:Math2 がテンプレート:Math の倍数であるときまたそのときに限ってテンプレート:Math2 という[[整数の合同|関係テンプレート:Math]] を決めると、これは同値関係になる。

この関係によって集合テンプレート:Mathbf が3つの同値類（この場合、剰余類 とも呼ばれる）に分割される。それぞれの同値類はテンプレート:Math で割り切れるもの全体テンプレート:Math、テンプレート:Math 余るもの全体テンプレート:Math、テンプレート:Math 余るもの全体テンプレート:Math に対応している。

この商集合は普通テンプレート:Math と書かれて、自然に演算が定義できて、加法に関するアーベル群、さらに乗法をいれて可換環になる（剰余類環）。またテンプレート:Mvar が素数のときテンプレート:Math は体（有限体）になる。

同様の例として、商線型空間（商ベクトル空間）、剰余群（剰余類群、商群）、剰余環（商環）、商位相空間などはそれぞれ適当な同値関係による商集合（に適切な構造を付与したもの）として定義される。

他の2項関係との関係

半順序は反射的・テンプレート:Underlineかつ推移的な二項関係をいう。
相等関係は半順序かつ同値関係となるような関係である。また、相等関係は反射的・対称的かつ反対称的な唯一の関係である。
狭義半順序は、非反射的・推移的かつ非対称的をいう。
テンプレート:仮リンクは推移的かつ対称的である。推移性と対称性から反射性が出るための必要十分条件は、各元テンプレート:Math2 に対して適当なテンプレート:Math2 をとればテンプレート:Math2 とできることである。
反射的かつ対称的な関係は、それが有限なときテンプレート:仮リンクといい、無限なときテンプレート:仮リンクという。
テンプレート:仮リンクは反射的かつ推移的な関係をいう。
合同関係は適当な代数系の台集合上で定義される同値関係で、付随する代数構造と両立するようなものをいう。一般に、合同関係は準同型の核と同じ役割を果たすもので、それによる商集合に商代数系の構造を入れることができる。多くの重要な場合において合同関係は考えている構造の部分構造として実現することができる（例えば、群の合同関係は正規部分群に対応する）。

ユークリッド関係

ユークリッドの著『原論』には

公理 1: 同じものに等しいもの同士は互いに等しい

という公理がある。今日において、上の公理の「等しい」という部分をすべて「関係する」と書き換えた性質を満足する関係はテンプレート:仮リンクであると言われる。二項関係テンプレート:Mvar に関して一般にはテンプレート:Mvar はテンプレート:Mvar と相異なるから、ユークリッド関係も

左ユークリッド関係：(テンプレート:Mvar かつテンプレート:Mvar) ならばテンプレート:Mvar
右ユークリッド関係：(テンプレート:Mvar かつテンプレート:Mvar) ならばテンプレート:Mvar

の二種類が考えられる。ユークリッド関係と同値関係との関係は以下のように述べることができる:

定理: 与えられた左（または右）ユークリッド関係が反射的ならば、その関係は対称的かつ推移的となる。

証明は以下のようにすればよい。

左ユークリッド関係の性質 [(テンプレート:Mvar かつテンプレート:Mvar) ならばテンプレート:Mvar] においてテンプレート:Math2 ととれば、[(テンプレート:Mvar かつテンプレート:Mvar) ならばテンプレート:Mvar] を得る。いま仮定によりテンプレート:Mvar は反射的だから恒真となるテンプレート:Mvar を除去すれば対称性 [[[:テンプレート:Mvar]] ならばテンプレート:Mvar] を得る。
対称性が示されたから、左ユークリッド関係の性質 [(テンプレート:Mvar かつテンプレート:Mvar) ならばテンプレート:Mvar] においてテンプレート:Mvar をテンプレート:Mvar で置き換えて推移性 [(テンプレート:Mvar かつテンプレート:Mvar) ならばテンプレート:Mvar] を得る。

右ユークリッド関係についても同様。ゆえに、同値関係は反射的かつユークリッド的な二項関係として特徴づけられる。

一般化

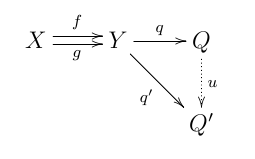
集合テンプレート:Mvar 上に同値関係テンプレート:Math が与えられたとする。テンプレート:Math2 とおき、写像テンプレート:Math2 をテンプレート:Math2, テンプレート:Math2 で定義すると、商集合テンプレート:Math と標準射影テンプレート:Math2 の組は集合の圏におけるテンプレート:Math とテンプレート:Math の余等化子である。

出典

テンプレート:脚注ヘルプテンプレート:Reflist

参考文献

テンプレート:Citation

外部リンク

テンプレート:Normdaten

↑ Garrett Birkhoff and Saunders Mac Lane, 1999 (1967). Algebra, 3rd ed. p.35, Th.19. Chelsea.
↑ Wallace, D. A. R., 1998. Groups, Rings and Fields. p. 31, Th. 8. Springer-Verlag.
↑ Dummit, D. S., and Foote, R. M., 2004. Abstract Algebra, 3rd ed. p. 3, Prop. 2. John Wiley & Sons.
↑ Karel Hrbacek & Thomas Jech (1999) Introduction to Set Theory, 3rd edition, pages 29–32, Marcel Dekker
↑ ProofWiki: Trivial_Relation, Trivial_Relation_is_Equivalence
↑ テンプレート:Citation. Sect. IV.9, Theorem 12, page 95
↑ テンプレート:Cite book

[1] Garrett Birkhoff and Saunders Mac Lane, 1999 (1967). Algebra, 3rd ed. p.35, Th.19. Chelsea.

[2] Wallace, D. A. R., 1998. Groups, Rings and Fields. p. 31, Th. 8. Springer-Verlag.

[3] Dummit, D. S., and Foote, R. M., 2004. Abstract Algebra, 3rd ed. p. 3, Prop. 2. John Wiley & Sons.

[4] Karel Hrbacek & Thomas Jech (1999) Introduction to Set Theory, 3rd edition, pages 29–32, Marcel Dekker

[5] ProofWiki: Trivial_Relation, Trivial_Relation_is_Equivalence

[6] テンプレート:Citation. Sect. IV.9, Theorem 12, page 95

[7] テンプレート:Cite book

[1]

[2]

[3]

[4]

[5]

[6]

[7]

同値関係

目次

定義

同値関係の例

諸概念

同値類

商集合

類別

同値核

同値関係の比較

商集合の例

他の2項関係との関係

ユークリッド関係

一般化

出典

参考文献

関連項目

外部リンク

ナビゲーションメニュー

同値関係

定義

同値関係の例

諸概念

同値類

商集合

類別

同値核

同値関係の比較

商集合の例

他の2項関係との関係

ユークリッド関係

一般化

出典

参考文献

関連項目

外部リンク

ナビゲーション メニュー

検索

ナビゲーションメニュー