自由エネルギー原理

自由エネルギー原理（じゆうエネルギーげんり、英：Free energy principle）は、脳の働きに関する理論的枠組みであり、脳が 内部モデルに基づいて予測を行い、感覚入力を用いてそのモデルを更新することで、テンプレート:仮リンク（テンプレート:仮リンクのこと）や不確実性を低減する と示唆する。この原理で強調される脳の目的は、内部モデルと外界との整合性を高めて予測の正確性を向上させることである。この原理はベイズ推定とテンプレート:仮リンクを統合しており、予測によって行動が導かれ、その行動がもたらす感覚フィードバックによって予測が精緻化されるとする。この原理は、脳機能、知覚、および行動の理解に広範な影響を与える。

概要

生物物理学および認知科学において、自由エネルギー原理は一つの数学的原理であり、物理システムの表象能力についての形式的な記述を提供する。つまりこれは、存在するものが、あたかもそれと結びつけられたシステムの特性の跡をたどっているように見える理由を説明するものである。この原理により規定されているのは、物理システムはその動態としてテンプレート:仮リンクとして表わされる驚きの度合い（ある結果の負の対数確率）を最小化すること、言い換えればその変分上界である自由エネルギーを最小化するということ である。この原理は特にテンプレート:仮リンクで用いられ、人工知能への取組みにも用いられる。また、テンプレート:仮リンクと密接に関連しており、もともとはテンプレート:仮リンクによって、神経科学における身体的知覚-行動ループの説明として導入された。

自由エネルギー原理は、あるシステムが他のシステム（例えば、システムが埋め込まれた環境）と分けられてはいるが離れがたく結びついているような場合に、そのシステムの振る舞いをモデル化する。このとき、システムと外界をつなぐ界面を十分に表現できる自由度を持った変数の集合をテンプレート:仮リンクと呼ぶ。より形式的に言うと、自由エネルギー原理が示しているのは、システム全体が「固有の分割」（いいかえれば、マルコフブランケットによる粒子への分割）を持つ場合、システムの部分集合が他の部分集合の統計的な構造の跡をたどる　という事である。この統計的な構造は、内部と外部の状態、またはシステムの経路として知られている。

自由エネルギー原理は、脳が推論エンジンであるとするベイズ的な考え方に基づいている。この原理の下では、システムは驚きが最小になる経路を追い求める。表現を変えると、システムは自身の世界モデルに基づく予測と、感覚および関連する知覚との差を最小にしている。この差は変分自由エネルギーとして定量化され、システムの世界モデルの継続的な修正、または世界をシステムの予測に近づけることで最小化される。つまり、システムが自由エネルギーを最小化するには、世界モデルを変えるのでは無く、世界そのものを能動的に変え、期待される状態に近づけるという方法もあるということである。

フリストンはこのことを、すべての生体反応の原理とみなす。また、フリストンは彼の原理が精神疾患や人工知能にも当てはまると信じている。能動的推論原理に基づく人工知能の実装は、他の方法に対して優位性を示している。

自由エネルギー原理は情報物理学の数学的原理であり、最大エントロピー原理や最小作用の原理に似て、数学的な観点から真である。自由エネルギー原理を否定しようとするのはカテゴリー誤認であり、経験的観測により微積分を否定しようとするのと同類である。（こういうやり方では数学的理論の間違いを示すことはできない；必要なのは理論から形式的矛盾を導くことである。）2018年のインタビューで、フリストンは　自由エネルギー原理が反証の対象ではないということを以下のように説明した：

私はここで基本的な区別をしておくことが有用だと思います。この区別は、言明と過程の理論との違いなのです；つまり、物事が従うかもしれない規範的な原理と、その原理がどのように実現されるかについての過程の理論すなわち仮説との違いなのです。

この区別の下では、自由エネルギー原理はテンプレート:仮リンクやベイズ脳仮説などとは全く別のものです。なぜなら自由エネルギー原理は原理だからです。ハミルトンの最小作用の原理のように、この原理も反証できず、否定できません。

実際、それに対してできることはあまりなく、測定可能なシステムがこの原理に従うかどうか問う以外にはありません。一方で、脳がベイズ推定や予測符号化のような形で行動するという仮説は、まさに仮説であり、経験的証拠で支持されることもあれば、されないこともあります。

経験的な証拠に支持された、このような仮説の例は多い。

背景

細胞や脳のような自己組織化する生体システムは、変分自由エネルギーを最小化するものとして理解できる という考え方は、ヘルムホルツのテンプレート:仮リンクに関する研究や、その後の 心理学および 機械学習における研究に基づいている。変分自由エネルギーは、観測値群と、それらの隠れた原因に対する確率密度の 関数である。この変分確率密度は、仮定された原因から観測結果を予測して生成する確率モデルに関連して定義される。この文脈において、自由エネルギーはテンプレート:仮リンクの近似を提供する。 したがって、その最小化はベイズ推論プロセスと見なすことができる。システムが自由エネルギーを最小化するために能動的に観測を行うとき、それは暗に能動的推論を実行し、自身の世界モデルの証拠を最大化する。

しかしながら、自由エネルギーは結果の自己情報量の上界でもあり、驚きの長期的平均はエントロピーである。これは、自由エネルギーの最小化を行うとき、システムは、サンプリングした結果（または感覚状態）のエントロピーの上界を（暗に）置くことになることを意味している。

他の理論との関係

能動的推論は、テンプレート:仮リンクや、自己組織化に関する報告と密接に関連している。自己組織化に関する報告には、自己集合、テンプレート:仮リンク、オートポイエーシス、およびテンプレート:仮リンクが含まれる。能動的推論は、サイバネティックス、テンプレート:仮リンク、および身体化された認知で検討されたテーマを扱っている。

自由エネルギーは、ある変分確率密度の下で観測が期待されるエネルギーから、そのエントロピーを引いた形で表せるので、最大エントロピー原理とも関連がある。さらに、エネルギーの時間平均は作用になるため、最小変分自由エネルギー原理は 結局のところ、最小作用の原理である。

スケール不変性を可能にする能動的推論は、他の理論や分野にも応用されている。例えば、社会学、言語学およびコミュニケーション、記号学、疫学など、多様な領域で適用されている。

また、負の自由エネルギーは、テンプレート:仮リンクと数学的に等価である。これは、機械学習において変分オートエンコーダなどの生成モデルを教育する際に広く使用される。

行動と知覚

図1: これらの模式図は、状態を内部状態(Internal states) $\mu (t)$ と外部状態(External [Hidden, Latent] states) $\psi (t)$ （隠れた潜在状態）に分割し、それらがマルコフブランケットによって分離されることを示している。マルコフブランケットは、感覚状態 $s(t)$ と行動状態 $a(t)$ から構成される。　上段の図は、まったく同じ依存関係を示しているが、細胞にあてはまるように配置し直されている。ここでは、内部状態が細胞内側の状態に対応し、感覚状態は細胞膜の表面状態となり、そのすぐ内側に行動状態（例：細胞骨格のアクチンフィラメント）が存在する形になっている。　下段の図は、この分割が脳における行動と知覚に適用される様子を示している。ここでは、行動状態(Active states, 図中ではAction)と内部状態(Internal states)が、感覚状態(sensory states, 図中ではSensation)に関する自由エネルギー汎関数を最小化する。続いて起こる、内部状態の自己組織化が知覚に対応し、行動(Action)は脳の状態を外部状態へと戻す形で結びつける役割を果たす。

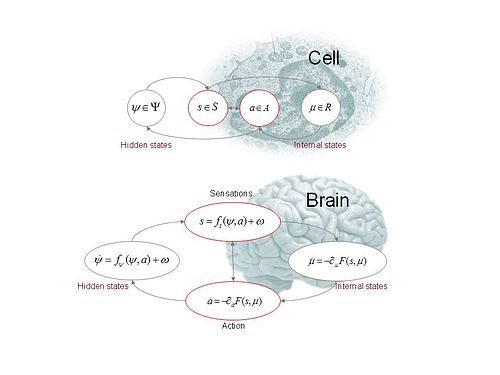
能動的推論は、生成的モデルから得られる感覚データの原因を、テンプレート:仮リンクの手法を適用して推論し、それらの推論の結果を行動の指針として用いる。

ベイズの定理は、このような因果モデルの確率論的に最適な反転（結果から原因を推定すること）を定式化するが、その適用は一般に計算的に困難である。そのため、実用的には近似的な手法が用いられることが多い。

能動的推論においては、こうした近似手法の中でも変分法が主要な役割を果たす。これは実践的および理論的な理由によるものである。実践的な理由として、変分法はしばしば単純な推論手続きを提供する点が挙げられる。一方、理論的な理由として、この手法が上記で説明したような物理学の基本原理と関連している点がある。

これらの変分法は、ベイズ最適推論（または事後確率）とその近似との 違い の 上限 を最小化することで進んでいく。この上限は自由エネルギーとして知られている。この概念に基づき、知覚は、入力される感覚情報について自由エネルギーを最小化する過程として特徴づけることができる。一方、行動は、出力される行動情報について同じ自由エネルギーを最小化する過程として捉えることができる。

このような全体として双対な最適化は、能動的推論の特徴である。そして、自由エネルギー原理は、「知覚し、行動するすべてのシステムは、この方法で記述できる」という仮説である。

生成モデルの定義

自由エネルギー原理を通じて能動的推論の仕組みを具体的に説明するためには、生成モデルを明確に定義する必要がある。この生成モデルは、複数の確率密度関数を含み、それらが組み合わされて因果モデルを特徴づける。

その一例として次のように定義される。

状態空間：

システムは状態空間 $X$ に存在するものとしてモデル化される。これは、システムのある状態はこの空間の点として表わされるという意味である。次に、この状態空間は以下のように因子分解される：

$X=\mathrm{\Psi }\times S\times A\times R$　

ここで、

• $\mathrm{\Psi }$ は、エージェントにとって「隠された」外部状態の空間であり、この状態には直接的な知覚やアクセスができない。
• $S$ は、エージェントが直接知覚する感覚状態の空間である。
• $A$ は、エージェントが取りうる行動の空間である。
• $R$ は、エージェントにとって内部状態の空間であり、外部には公開されない。

図1に従い、以後 $\dot{\psi },\psi ,s,a$ と $\mu$ は（連続な）時間 $t$ の関数であることに注意する。生成モデルは次に示す確率密度関数によって具体的に定義される。

感覚モデル:

$p_S:S\times \mathrm{\Psi }\times A\to ℝ$　　これは通常次の ように記述される：　$p_S(s\mid \psi ,a)$

この関数は、外部状態 $\psi$ と行動 $a$ を所与として感覚データ $s$ の確からしさ(尤度)を特徴づける。

環境動態の確率モデル:

$p_{\mathrm{\Psi }}:\mathrm{\Psi }\times \mathrm{\Psi }\times A\to ℝ$　　これは通常、以下のように記述される：$p_{\mathrm{\Psi }}(\dot{\psi }\mid \psi ,a)$

この関数は、エージェントの行動 a を所与として、外部状態 ψ が時間 t においてどのように変化すると予測されるかを特徴づける。

行動モデル:

$p_A:A\times R\times S\to ℝ$　　これは以下のように記述される：　$p_A(a\mid \mu ,s)$

この関数は、エージェントの行動 $a$ が、内部状態 $\mu$ と感覚データ $s$ にどのように依存するかを特徴づける。

内部状態モデル:

$p_R:R\times S\to ℝ$　　これは以下のように記述される：　$p_R(\mu \mid s)$

この関数は、エージェントの内部状態 $\mu$ が感覚データ $s$ にどのように依存するかを特徴づける。

結合モデル：

これらの確率密度関数は、「結合モデル」の要素を決定する。この結合モデルは、生成モデルの完全な仕様を表すものであり、次のように記述される：　$p(\dot{\psi },s,a,\mu \mid \psi )=p_S(s\mid \psi ,a)p_{\mathrm{\Psi }}(\dot{\psi }\mid \psi ,a)p_A(a\mid \mu ,s)p_R(\mu \mid s)$.

能動的推論

事後確率密度

次に、ベイズの定理 に基づき、「事後確率密度」 $p_{\text{Bayes}}(\dot{\psi }|s,a,\mu ,\psi )$ が決定される。この事後確率密度は、直前の外部状態 $\psi$ と、エージェントの行動 $a$、感覚信号 $s$、および内部状態 $\mu$ を所与として、外部状態 $\dot{\psi }$ に関する確率論的に最適な信念を表す。

しかし、この事後確率密度 $p_{\text{Bayes}}$​の厳密な計算は手に負えないほど困難であるため、自由エネルギー原理では、 $p_{\text{Bayes}}$​ の近似となる「変分確率密度」$q(\dot{\psi }|s,a,\mu ,\psi )$ の存在を仮定する。

自由エネルギー

このとき、自由エネルギー は以下のように定義される。

$\begin{array}{cc}\underset{\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{-}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}}{\underbrace{F(\mu ,a;s)}}& =\underset{\text{expected energy}}{\underbrace{{𝔼}_{q(\dot{\psi })}[-\log p(\dot{\psi },s,a,\mu \mid \psi )]}}-\underset{\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{y}}{\underbrace{ℍ[q(\dot{\psi }\mid s,a,\mu ,\psi )]}}\\ & =\underset{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}{\underbrace{-\log p(s)}}+\underset{\mathrm{d}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}}{\underbrace{𝕂𝕃[q(\dot{\psi }\mid s,a,\mu ,\psi )\parallel p_{\text{Bayes}}(\dot{\psi }\mid s,a,\mu ,\psi )]}}\\ & \ge \underset{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}}{\underbrace{-\log p(s)}}\end{array}$

この式は、

自由エネルギー (free-energy) が、期待エネルギー (expected energy) から エントロピー (entropy) を 引いたものとして表されることを示しており、また、自由エネルギーを

• 驚き（surprise）：　$-\log p(s)$　（感覚データ $s$ の対数尤度の負の値）
• カルバック・ライブラー（KL）発散 (divergence)：　$𝕂𝕃[q\parallel p_{\text{Bayes}}]$ （変分確率密度 $q$ とベイズ事後確率 $p_{\text{Bayes}}$ との違いの尺度）

の和として表わすこともできることを示している。　

行動と知覚

そして、行動と知覚は、次のような同時最適化問題として定義される。

$\begin{array}{cc}{\mu }^{*}& =\underset{\mu }{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\{F(\mu ,a;s))\}\\ a^{*}& =\underset{a}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\{F({\mu }^{*},a;s)\}\end{array}$

• 内部状態 $\mu$ の最適値 ${\mu }^{*}$ は、自由エネルギー $F$ を最小化する $\mu$ の値として決定される。
• 行動 $a$ の最適値 $a^{*}$ は、最適な内部状態 ${\mu }^{*}$ を所与とした上で、自由エネルギー $F$ を最小化する $a$ の値として決定される。

ここで、内部状態 $\mu$ は通常、変分確率密度 $q$ のパラメーター群を符号化したものとみなされる。したがって、内部状態は、外部状態 $\mathrm{\Psi }$ についての事後信念に関するエージェントの最良の推測 を表すものとみなされる。

自由エネルギーは、エージェントの（ぎりぎり または 平均的な）感覚的驚きの上限でもあることに注意する。したがって、自由エネルギーの最小化は、驚きの最小化という観点からも動機づけられる。

自由エネルギーの最小化

自由エネルギーの最小化と自己組織化

自己組織化システムがテンプレート:仮リンクとみなせる場合、自由エネルギーの最小化がその特徴的な性質となる　という見方が提案されている。　この枠組みは、行動と感覚状態を含むテンプレート:仮リンクに基づいており、マルコフブランケットは内部状態と外部状態を分離する役割を果たすものである。　もし内部状態と行動が自由エネルギーを最小化するならば、それは感覚状態のエントロピーの上限を設定することになる：

$\underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\underset{\text{free-action}}{\underbrace{\underset{0}{\overset{T}{\int }}F(s(t),\mu (t))dt}}\ge \underset{T\to \mathrm{\infty }}{\lim }\frac{1}{T}\underset{0}{\overset{T}{\int }}\underset{\text{surprise}}{\underbrace{-\log p(s(t)\mid m)}}dt=H[p(s\mid m)]$

これは、エルゴード性の仮定のもとでは、長期的な驚きの平均がエントロピーと等しくなるためである。この上限は、（熱力学第二法則 や ゆらぎの定理に関連付けられた）無秩序への自然な傾向に対抗する。

　しかしながら、生命科学における統一原理を、ランダム力学系、非平衡定常状態、およびエルゴード性といった統計物理学の概念に基づいて定式化することは、生物システムを理論的・実証的に研究する上で重大な制約を課すことになる。その結果、生物システムを単なる自己組織化システムの中でも興味深いものとしている特性が、見えにくくなるというリスクが伴う。

自由エネルギーの最小化とベイズ推論

すべてのベイズ推論は、自由エネルギーの最小化という観点から記述できる。テンプレート:Failed verification自由エネルギーが内部状態について最小化されるとき、隠れ状態（外部状態）上で、変分確率密度と事後確率密度の間のカルバック・ライブラー（KL）発散が 最小化される。これは、変分確率密度の式が固定されている場合には近似的なベイズ推論となり、そうでない場合には厳密なベイズ推論　となる。

したがって、自由エネルギーの最小化は、ベイズ推論やフィルタリング（例：カルマンフィルター）を包括的に記述する方法を提供する。また、自由エネルギーの最小化は、ベイズテンプレート:仮リンクにも応用され、自由エネルギー(free-energy) は 複雑さ (complexity) と 正確さ (accuracy) の差に分解できる：

$\underset{\text{free-energy}}{\underbrace{F(s,\mu )}}=\underset{\text{complexity}}{\underbrace{D_{\mathrm{K}\mathrm{L}}[q(\psi \mid \mu )\parallel p(\psi \mid m)]}}-\underset{\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}}{\underbrace{E_q[\log p(s\mid \psi ,m)]}}$

最小自由エネルギーを持つモデルは、（複雑さのコスト（例：オッカムの剃刀 や、より形式的な計算コストの取り扱い　などを参照）の下ではあるが、）データを精密に説明する。ここで、複雑さ とは、ある隠れ状態の下で 変分確率密度と 事前信念 の間の相違である。すなわちこれは、データを説明するために使用される有効自由度 である。

自由エネルギーの最小化と熱力学

変分自由エネルギーは、情報理論的な関数であり、熱力学的な（ヘルムホルツ）自由エネルギーとは異なる。しかし、変分自由エネルギーの 複雑さ 項は、ヘルムホルツ自由エネルギーと同じ不動点を持つ（ただし、システムが熱力学的に閉じているが孤立していないと仮定した場合である）。その理由は、感覚的な外乱が（十分に長い時間にわたって）止められると、複雑さ が最小化されるためである（なぜなら、正確さ が無視できるからである）。このとき、システムは平衡状態 にあり、テンプレート:仮リンク に従って内部状態はヘルムホルツ自由エネルギーを最小化する。

自由エネルギーの最小化と情報理論

自由エネルギーの最小化は、感覚状態と、（エントロピーが固定されている場合の）変分確率分布のパラメーターとしての内部状態との間の、相互情報量を最大化することと等価である。これは、自由エネルギーの最小化が「最小冗長性原理」と関連していることを示す。

神経科学における自由エネルギー最小化

自由エネルギーの最小化は、不確実性のもとで神経が推論や学習を行うことを、標準（ベイズ最適）モデルとして定式化するための有用な方法である。したがって、自由エネルギーの最小化はテンプレート:仮リンクを支持する。自由エネルギーの最小化によって記述される神経過程は、以下のような隠れ状態の性質に依存する：

$\mathrm{\Psi }=X\times \mathrm{\Theta }\times \mathrm{\Pi }$

これは、時間に依存する変数と、時間不変なパラメーターと、確率的変動の精度（すなわち逆分散または温度）から成る。変数での最小化、パラメーターでの最小化、および 精度での最小化 は、それぞれ 推論、学習、不確実性の符号化 に対応する。

知覚推論とカテゴリー化

自由エネルギーの最小化は、知覚における テンプレート:仮リンク の概念を形式化し、神経細胞による処理（neuronal processing）に関する標準（ベイズ的）理論 を提供する。

ニューロンの動態（neuronal dynamics）の関連過程理論（associated process theory）は、自由エネルギーを勾配降下法 によって最小化することに基づいている。これは、テンプレート:仮リンク（generalised Bayesian filtering）に対応する（ここで、~　は 一般化運動座標の変数を、$D$ は 微分行列演算子 を表す）：

$\dot{\tilde{\mu }}=D\tilde{\mu }-{\partial }_{\mu }F(s,\mu ){|}_{\mu =\tilde{\mu }}$

通常、自由エネルギーを定義する 生成モデル は、非線形 かつ （脳の皮質の階層と似て）階層的 である。

一般化フィルタリング の特別なケースには、カルマンフィルター が含まれる。これは、テンプレート:仮リンク と形式的に等価であり、脳内でのメッセージ伝達の例えとしてよく知られている。

階層モデルのもとで、予測符号化には 上向き（ボトムアップ）の予測誤差 および 下向き（トップダウン）の予測の回帰的な交換が 伴う。このメカニズムは、感覚系 と 運動器系 の解剖学的・生理学的構造と一致している。

知覚学習と記憶

予測符号化 において、自由エネルギー（自由行動）の時間積分に対し、勾配降下法 を用いてモデルパラメーターの最適化をすることは、連合性可塑性（associative plasticity） またはヘッブ的可塑性（Hebbian plasticity）に帰着し、脳におけるシナプス可塑性（synaptic plasticity） と関連している。

知覚の精度、注意、顕著性

精度パラメーター（precision parameters）の最適化は、予測誤差のゲインの最適化に対応する（例えば、カルマンゲイン）。神経生理学的に妥当な予測符号化の実装では、この最適化は、浅層錐体細胞（superficial pyramidal cells）のテンプレート:仮リンクの最適化に対応し、注意のゲイン（attentional gain）として解釈されている。

複数の対象物が存在する環境において、SAIM（Selective Attention in Intelligence Model）のベイズ的再構成版である PE-SAIM によって実行された選択的注意課題の結果をシミュレーションした。　このグラフは、 FOA（Focus of Attention、注意の焦点）および2つのテンプレートユニットが、知識ネットワーク内で活性化する時間的推移 を示している。

注意に関するトップダウン vs. ボトムアップ論争は、主要な未解決問題として取り上げられてきた。この課題に対し、ある計算モデルが、トップダウンとボトムアップのメカニズムが相互作用する 循環的な性質 を示すことに成功した。注意の創発モデル（emergent model of attention）として確立された SAIM というモデルを用いて、著者らはPE-SAIM というモデルを提案した。これは標準版とは対照的に、選択的注意 にトップダウン的な視点からアプローチする。このモデルは、予測誤差を同じレベルまたは上位レベルへ伝達することを考慮に入れている。これは、データ と その原因（または、生成モデル と 事後確率）との間の差を示すエネルギー関数を最小化するためである。モデルの妥当性を高めるために、著者らは刺激間の神経競合（neural competition）も組み込んだ。このモデルの顕著な特徴は、課題実行中において、自由エネルギー関数を予測誤差のみを用いて再定式化した点である。：

$\frac{\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y_{mn}^{SN}}=x_{mn}^{CN}-b^{CN}{\epsilon }_{nm}^{CN}+b^{CN}\sum _k({\epsilon }_{knm}^{KN})$

ここで、$E^{total}$ は神経ネットワークが含む総エネルギー関数（total energy function） を表す。また、${\epsilon }_{knm}^{KN}$ は、生成モデル（事前確率）と事後確率 との間の予測誤差 であり、時間とともに変化する。両モデル（SAIMとPE-SAIM）を比較すると、それぞれの結果の間に顕著な類似性が見られる一方で、際立った違いも浮かび上がる。具体的には、標準版のSAIMでは、モデルの焦点が主に興奮性結合に置かれているのに対し、PE-SAIMでは、抑制性結合を推論のために活用している。このモデルはまた、人間の実験から得られた EEG（脳波）および fMRI（機能的磁気共鳴画像）のデータを高精度で予測できることが示された。同様に、Yahya らは、自由エネルギー原理を適用し、主に SAIM に依拠する「潜在的選択的視覚注意（covert selective visual attention）」におけるテンプレートマッチング（template matching）の計算モデルを提案した。

この研究によれば、全状態空間の総自由エネルギー は、元の神経ネットワークにトップダウン信号を挿入することで達せられる。これにより、テンプレート:仮リンクとフィードバックの両方の予測誤差を含む動的システムが導き出される。

能動的推論

勾配降下法 が行動 $\dot{a}=-{\partial }_{a}F(s,\tilde{\mu })$ に適用される場合、運動制御 は、下行性（皮質脊髄性）の予測によって活性化される 古典的な反射弓の観点から理解することができる。 この枠組みは、平衡点解の自由度問題への一般化や、運動軌道への一般化　のための形式を提供する。

能動的推論と最適制御

能動的推論 は、最適制御と関連する。この関連は、最適制御の価値関数やコスト関数を、状態遷移 または流れに関する事前信念に置き換えることで得られる。これは、ベイズフィルタリングと、ベルマン方程式 の解 との密接な関係を活用して行われる。　しかし、能動的推論 は、以下の 流れについての事前確率分布から始まる：

$f=\mathrm{\Gamma }\cdot \mathrm{\nabla }V+\mathrm{\nabla }\times W$

　これは、状態空間におけるスカラー関数$V(x)$  およびベクトル関数$W(x)$  で指定される（ヘルムホルツ分解　を参照のこと）。

　ここで、$\mathrm{\Gamma }$ はランダム変動の振幅を表し、コストは以下の式で定義される：

$c(x)=f\cdot \mathrm{\nabla }V+\mathrm{\nabla }\cdot \mathrm{\Gamma }\cdot V$ 。

流れ についての事前確率分布 $p(\tilde{x}\mid m)$ は、次のような状態についての事前確率分布を誘導する ：

$p(x\mid m)=\exp (V(x))$

　これは、適切な順方向テンプレート:仮リンク の解となる。

対照的に、最適制御 はコスト関数を所与とし、以下の仮定のもとで流れを最適化する：$W=0$（これは、流れは テンプレート:仮リンク または 詳細釣り合い を満たす事を示している）。通常、この方法では逆方向コルモゴロフ方程式 を解く必要がある。

能動的推論と最適意思決定（ゲーム）理論

テンプレート:仮リンク問題（通常、部分観測マルコフ決定過程 として定式化される）は、能動的推論 の枠組みにおいて、効用関数を事前信念に組み込むことで処理される。　この設定において、エージェントが期待するのは、高い効用（低いコスト）を持つ状態を占めること である。　生成モデル に、制御をモデル化する隠れ状態 を組み込むことで、変分自由エネルギーを最小化する方策（制御系列）は、高い効用を持つ状態に至る。

神経科学的に、ドーパミンなどのテンプレート:仮リンク物質 は、予測誤差を符号化する主細胞のゲインを調整することで、予測誤差の精度を伝達すると考えられている。これは、形式的には異なるものの、ある意味でドーパミン が予測誤差を伝達する役割や　関連する計算論的説明と密接に関連している。

能動的推論と認知神経科学Active inference and cognitive neuroscience

能動的推論は、認知神経科学、脳機能、および神経精神医学 におけるさまざまな問題に対処するために使用されてきた。これには、以下が含まれる：行動観察、ミラーニューロン、テンプレート:仮リンク（saccades）と視覚探索、テンプレート:仮リンク、睡眠、錯覚、注意、テンプレート:仮リンク、意識、ヒステリー、精神病。　能動的推論における行動の説明は、しばしば「頑固な予測（stubborn predictions）」 という概念に依存している。この予測は更新できず、結果として、これらの予測が実現するような行動を引き起こす という概念である。

関連項目See also

• アフォーダンス
• エントロピー的な力
• テンプレート:仮リンク
• 決定理論
• テンプレート:仮リンク
• テンプレート:仮リンク - 自然（生物および無生物）における設計進化の法則
• テンプレート:仮リンク
• 最適制御
• 自己組織化
• テンプレート:仮リンク
• テンプレート:仮リンク
• テンプレート:仮リンク
• 身体化された認知
• テンプレート:仮リンク
• テンプレート:仮リンク
• テンプレート:仮リンク
• テンプレート:仮リンク

外部リンク

• Behavioral and Brain Sciences (by Andy Clark)