マグマ (数学)
テンプレート:代数的構造 抽象代数学におけるマグマ(テンプレート:Lang-en-short)または亜群(あぐん、テンプレート:En)とは、一つの集合と、その集合上に閉じて定義された一つの二項演算で構成される組(代数的構造)である。
このような構造に「マグマ」という呼称を導入したのはニコラ・ブルバキである。旧来はテンプレート:Illによる用語で亜群(テンプレート:En)と呼ばれていたもので、現在でもしばしばそのように呼ばれる。(ただし、圏論において、「テンプレート:Ill(テンプレート:En)」と呼ばれる全く別の概念もある。) テンプレート:Group-like structures
定義
マグマ (M, μ) とは、集合 M と、M 上での閉性(M の元 a, b のどの組み合わせについても、μ(a, b) がまた M の元であること)を満たす二項演算 μ を、組として考えたものである。二項演算 μ は、集合 M 上での閉性のほかに公理を課されない。
演算が明らかで紛れのおそれが無いときは、演算の記号を落として台集合の記号のみによってマグマ M などとも表す。しばしば二項演算 μ はマグマ M における乗法とも呼ばれ、このときの演算結果 μ(a, b) は a と b との積という[* 1]。また、誤解のおそれが無いならば積 μ(a, b) は演算記号を省略してしばしば ab と書かれる。演算記号が省略されている場合に、マグマが台集合と演算の対であることを明示するにはプレースホルダを用いて (M, ·) のように書かれる。
演算 μ が偏演算(局所演算、部分演算)ならば、(M, μ) を局所マグマ(偏マグマ)という[* 2]。
部分マグマ
マグマ (M, μ) の台集合 M の部分集合 N が μ とマグマを成すならば、マグマ (N, μ) を (M, μ) の部分マグマ(テンプレート:En)という。
マグマ準同型
ふたつのマグマ (M, μ), (N, ν) の間の準同型写像(テンプレート:En)またはマグマ準同型とは写像 f: M → N であって、
なる意味でマグマの二項演算を保つものをいう。マグマ準同型 f: M → N が全単射ならば f の逆写像 fテンプレート:Sup- N → M もまたマグマ準同型であり、M と N はマグマとして同じ構造を持つと考えられる。このとき、f(および fテンプレート:Sup-)をマグマ同型写像(テンプレート:En)またはマグマ同型と呼び、ふたつのマグマ M と N は互いに同型(テンプレート:En)であるという。
マグマ合同と剰余マグマ
マグマ (M, μ) と台集合 M 上の同値関係 ∼ が与えられているとき、同値関係 ∼ がマグマ合同であるとは
が任意の x, y, u, v ∈ M に対して成り立つという意味でマグマ演算 μ と両立することをいう。∼ がマグマ合同であるとき、∼ による合同類の全体
に二項演算 μテンプレート:' が
とおくことにより矛盾なく定まり、(M/∼, μテンプレート:') は再びマグマを成す。これをマグマ M のマグマ合同 ∼ による剰余マグマ(テンプレート:En)、商マグマ(テンプレート:En)、因子マグマ(テンプレート:En)などと呼ぶ。
結合順序の組合せ論
一般の非結合的な場合のマグマ演算を繰り返し反復適用することを考え、演算を適用する対を表すのに括弧を用いる。演算を繰り返して得られた文字列は、マグマの元を表す記号と開閉の対応のとれた括弧からなるものとなる。対応のとれた括弧からなる可能な限りの文字列全体の成す集合はダイク言語と呼ばれる。マグマ演算を n-回適用して得られる相異なる文字列の総数はカタラン数 Cn で与えられる。したがって例えば、C2 = 2 であることから、マグマの三つの元に二回演算を適用するときの組合せは
- (ab)c または a(bc)
のふた通りしかないことがわかる。
表記の簡略化のためしばしば括弧の数を減らすことが行われる。これは演算を適用する場所でだけ文字を併置することで実現される。たとえば、マグマ演算を中置記法で ∗ とすると、xy ∗ z が (x ∗ y)∗ z の簡略表示である。さらなる簡略化は空白の挿入・抜取によるもので、例えば、xy∗z ∗ wv によって ((x ∗ y) ∗ z) ∗ (w ∗ v) が表せる。もちろん、もっと複雑な式に対しては、括弧の使用は不可避のものとなる。括弧の使用を完全に避ける方法としては、演算を中置記法で記すのではなく、前置記法や後置記法によればよい。
自由マグマ
集合 X 上の自由マグマ(テンプレート:En)とは集合 X から生成されるマグマのうち「可能な限り最も一般」なもの(つまり、元を生成するときに、生成された元の間に何の関係や公理も課さないという意味で自由なマグマ)をいう。これは、X を字母集合としたとき、括弧を保った非結合的な語の集合とみなすこともできる。また、計算機科学でよく用いられる概念をつかえば、自由マグマは、葉ノードがそれぞれ X の元でラベル付けられた二分木全体の集合であると見ることもできる。この見方をするとき、マグマ演算は二つの木を根と根で結合する操作に対応する。したがって、これは構文論において基礎的な役割を演じる。
自由マグマのもつ「可能な限り最も一般」という性質(普遍性)は次のように表すことができる。
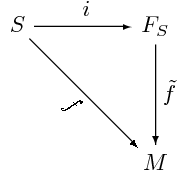
- 集合 S から任意のマグマ M への写像 f: S → M が与えられたとき、f は S 上の自由マグマ FS から M へのマグマ準同型に一意的に拡張される。
すなわち、任意のマグマはある自由マグマのマグマ準同型像(同じことだが剰余マグマ)にマグマ同型である。
マグマのクラス

各頂点は テンプレート:Bulleted list各矢印はテンプレート:Bulleted list 可除性も可逆性も消約性の成立を含意することに注意。
一般には、マグマをそのままマグマとして調べるということはまずあり得ず、代わりに(部分的なクラスに分けるために)マグマの二項演算に適当な公理を課した、いくつかの別な種類の代数系として調べることになる。よく知られたクラスの、特別な名前が付いている代数系としては
- 準群: 空でないマグマで除法が常にできるもの。
- ループ: 単位元を持つ準群。単位的準群。
- 半群: 演算が結合的なマグマ。
- モノイド: 単位元をもつ半群。単位的半群。
- 群: 逆元を持つモノイド。
- アーベル群: 演算が可換な群。
といったようなものを挙げることができる。もちろん、特別な呼び方はなくとも、可換マグマや可換モノイドといったような代数系のクラスもしばしば扱われる。
更なる定義
マグマ M が、[* 3]
- 単位的(テンプレート:En)であるとは、それが単位元を持つときにいう。
- 中可換(テンプレート:En)であるとは、恒等式 (xy)(uz) = (xu)(yz) を満たすときにいう。
- 左半中可換(テンプレート:En)であるとは、恒等式 (xx)(yz) = (xy)(xz) を満たすときにいう。
- 右半中可換(テンプレート:En)であるとは、恒等式 (yz)(xx) = (yx)(zx) が満たされるときにいう。
- 半中可換(テンプレート:En)であるとは、左中可換かつ右中可換であるときにいう。
- 左分配的(テンプレート:En)であるとは、恒等式 x(yz) = (xy)(xz) を満たすときにいう。
- 右分配的(テンプレート:En)であるとは、恒等式 (yz)x = (yx)(zx) が満足されるときにいう。
- 両側分配的(テンプレート:En)であるとは、左分配的かつ右分配的であるときにいう。
- 可換(テンプレート:En)であるとは、xy = yx なる恒等式が成立するときにいう。
- 冪等(テンプレート:En)であるとは、xx = x が恒等的に成り立つときに言う。
- 単冪(テンプレート:En)であるとは、恒等的に xx = yy となるときにいう。
- 零冪(テンプレート:En)であるとは、恒等式 (xx)y = y(xx) = xx が成立するときにいう。
- 左交代的(テンプレート:En)であるとは、恒等式 (xx)y = x(xy) が成立するときにいう。
- 右交代的(テンプレート:En)であるとは、恒等式 y(xx) = (yx)x が成立するときにいう。
- テンプレート:仮リンク(テンプレート:En)であるとは、左交代的かつ右交代的であるときにいう。
- 冪結合的(テンプレート:En)であるとは、その任意の元の生成する部分マグマが必ず結合的となるときにいう。
- 左消約的(テンプレート:En)であるとは、等式 xy = xz から常に y = z が帰結できるときにいう。
- 右消約的(テンプレート:En)であるとは、等式 yx = zx から y = z が常に帰結されるときにいう。
- 消約的(テンプレート:En)であるとは、それが左消約的かつ右消約的となるときにいう。
- 半群(テンプレート:En)または結合的(テンプレート:En)であるとは、x(yz) = (xy)z が恒等式であるときにいう。
- 左零付き半群(テンプレート:En)であるとは、x = xy を恒等的に満足する元 x が存在するときにいう。
- 右零付き半群(テンプレート:En)であるとは、x = yx が恒等的に成立するような元 x がとれるときにいう。
- 零半群 テンプレート:En であるとは、恒等式 xy = uv を満たすときにいう。
- left unar であるとは、恒等式 xy = xz が満足されるときにいう。
- right unar であるとは、yx = zx なる恒等式が成立するときにいう。
- trimedial であるとは、その任意の三元(必ずしも相異なる必要はない)が生成する部分マグマが中可換であるときにいう。
- entropic であるとは、ある中可換消約マグマの準同型像となっているときにいう。
一般化
テンプレート:仮リンクを見よ。
関連項目
注記
- ↑ 数の乗法および積の用語を流用したものではあるが、一般にはそれらの概念と直接的な関係は無い。
- ↑ 写像ではなく、定義域と始域が一致しない部分写像(テンプレート:En)となっているような演算を偏演算(テンプレート:En)という。"partial" には「部分」「偏」などの訳語が当てられることが多いが、これを「部分マグマ」とよぶと "submagma" と紛らわしい。テンプレート:Harv では「偏亜群」等
- ↑ 各訳語はおおかた テンプレート:Harv に従った。
参考文献
外部リンク
- テンプレート:Nlab
- 代数系への入門 (PDF): 広島大学 2004-2009各年度代数学講義用レジュメ、松本研究室
- 『数学ガール』ミルカさんとコンボリューション (PDF): 結城浩著、物語形式の数学読物のシリーズの一作。括弧のつけ方がテーマの回。とくに3節と7節およびあとがき。