写像の微分

数学の一分野、微分幾何学における多様体間の写像の微分(びぶん、テンプレート:Lang-en-short)または全微分 (テンプレート:En) は、通常の解析学における全微分の概念を可微分写像に対して一般化するもので、可微分多様体間の可微分写像のある意味での最適線型近似を各点において与えるものである。より具体的に、可微分多様体 テンプレート:Mvar の間の可微分写像 テンプレート:Math に対し、テンプレート:Mvar の テンプレート:Math における微分(係数) テンプレート:Mvar は、テンプレート:Mvar における テンプレート:Mvar の接空間から テンプレート:Math における テンプレート:Mvar の接空間への線型写像として与えられる。
各点における微分係数 テンプレート:Mvar は、接束を考えることにより、テンプレート:Mvar を動かして微分写像(導写像)テンプレート:Mvar にすることができる。テンプレート:Mvar は接写像とも呼ばれ、可微分多様体の接束をとる操作(接構成)は接写像を伴って可微分多様体の圏からベクトル束の圏への函手(接函手)を定める。
動機付け
多変数微分積分学において既知の事実として、写像 テンプレート:Math が テンプレート:Math の開集合 テンプレート:Mvar から テンプレート:Math の開集合 テンプレート:Mvar への可微分函数であるとき、テンプレート:Mvar の各点 テンプレート:Mvar において テンプレート:Mvar の全微分すなわち テンプレート:Math なる線型写像は、(標準基底に関して)ヤコビ行列によって表現されるのであった。
このことが任意の多様体 テンプレート:Mvar の間の可微分写像 テンプレート:Mvar に対する場合に一般化されることを見よう。
可微分写像の微分
可微分多様体間の可微分写像 テンプレート:Math を考えるとき、適当な点 テンプレート:Math が与えられれば、テンプレート:Mvar における テンプレート:Mvar の微分 (differential) は テンプレート:Mvar の テンプレート:Mvar における接空間から テンプレート:Mvar の テンプレート:Math における接空間への線型写像 テンプレート:Math として与えられる。微分 テンプレート:Mvar を接ベクトル テンプレート:Mvar に作用させることは、テンプレート:Mvar による テンプレート:Mvar の押し出し (pushforward) とも呼ばれる。
微分あるいは押し出しの、正確な定義は接ベクトルの定義の仕方に依存する(接ベクトルの様々な定義の仕方は接空間の項を参照)。
- 接ベクトルを、テンプレート:Mvar を通る曲線の同値類として定義した場合には、上記の微分は テンプレート:Math によって与えられる。ここに テンプレート:Mvar は テンプレート:Math を満たす テンプレート:Mvar 内の曲線である。言い換えれば、曲線 テンプレート:Mvar の テンプレート:Math における接ベクトルの押し出しは、曲線 テンプレート:Nowrap の テンプレート:Math における接ベクトルによって与えられる。
- 同じことだが、接ベクトルを実数値可微分函数の空間に作用するテンプレート:仮リンクとして定義した場合には、微分は テンプレート:Math によって与えられる。ここに、テンプレート:Math は テンプレート:Mvar 上定義された導分で、テンプレート:Mvar は テンプレート:Mvar 上の実数値可微分函数である。定義により、各点 テンプレート:Math における テンプレート:Mvar の押し出しは テンプレート:Math に属し、それ自体ひとつの導分となる。
さて テンプレート:Mvar および テンプレート:Math の周りのチャートを選べば、テンプレート:Mvar は局所的に テンプレート:Math の開集合 テンプレート:Mvar から テンプレート:Math の開集合 テンプレート:Mvar への可微分函数 テンプレート:Math によって決定され、テンプレート:Mvar における微分 テンプレート:Mvar は
と表現される(ただしアインシュタインの和の規約を用いた)。ここで偏微分は与えられたチャートにおいて テンプレート:Mvar に対応する テンプレート:Mvar の点において評価するものとする。これを線型に拡張して、テンプレート:Math-成分が
で与えられる行列を得る。これにより、微分 テンプレート:Mvar は、各点において可微分写像 テンプレート:Mvar に付随して決まる接空間の間の線型変換となるから、したがって適当な局所座標系を選んで、対応する テンプレート:Math から テンプレート:Math への可微分函数のヤコビ行列によって表現することができる。一般にはこの微分は可逆とは限らない。テンプレート:Mvar が局所微分同相写像ならば テンプレート:Mvar における押し出しは可逆であり、逆写像は テンプレート:Math のテンプレート:仮リンクによって与えられる。
この微分は テンプレート:Mvar, テンプレート:Math, テンプレート:Math, テンプレート:Mvar など様々な記法を用いて表されることがよくある。
定義から、合成写像の微分が、微分の合成に等しいことが従う(すなわち、微分をとる操作は函手的である)。つまり、
- 可微分写像の微分の連鎖律
- テンプレート:Math.
また、局所微分同相写像の微分は、接空間の間の線型同型となる。
接束上の微分写像
可微分写像 テンプレート:Mvar の微分 テンプレート:Mvar は、自然な仕方で テンプレート:Mvar を動かして、テンプレート:Mvar の接束から テンプレート:Mvar の接束へのテンプレート:仮リンク(実はテンプレート:仮リンク)テンプレート:Mvar または テンプレート:Math を誘導し、それは以下の図式
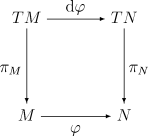
を可換にする。ただし、テンプレート:Mvar および テンプレート:Mvar はそれぞれ テンプレート:Mvar および テンプレート:Mvar の接束に関する束射影である。
あるいは同じこと(テンプレート:仮リンクの項参照)だが、テンプレート:Math は接束 テンプレート:Mvar からテンプレート:仮リンク テンプレート:Math への テンプレート:Mvar 上の束写像であり、これを テンプレート:Mvar 上の準同型束 テンプレート:Math の切断と見ることができる。この束写像 テンプレート:Mvar は テンプレート:Mvar とも書かれ、接写像 (tangent map) と呼ばれる。この方法(テンプレート:Math)で テンプレート:Mvar は函手となる。
ベクトル場の押し出し
可微分写像 テンプレート:Math と テンプレート:Mvar 上のベクトル場 テンプレート:Mvar が与えられたとき、テンプレート:Mvar の テンプレート:Mvar による押し出しを テンプレート:Mvar 上の適当なベクトル場と同一視することが普通はできない。例えば、写像 テンプレート:Mvar が全射でなければ テンプレート:Mvar の像に属さないところでそのような押し出しを定義する自然な方法がないし、また テンプレート:Mvar が単射でなければ与えられた点における押し出しの選び方が複数存在しうる。にもかかわらず、この困難を正確にして、写像に沿うベクトル場の概念が用いられる。
テンプレート:Mvar 上のベクトル束 テンプレート:Math の切断を テンプレート:Mvar に沿うベクトル場と呼ぶ。例えば、テンプレート:Mvar が テンプレート:Mvar の部分多様体で、テンプレート:Mvar が包含写像のとき、テンプレート:Mvar に沿うベクトル場とは テンプレート:Mvar の接束の テンプレート:Mvar に沿う切断のことに他ならない。特に、テンプレート:Mvar 上のベクトル場は テンプレート:Mvar の テンプレート:Mvar への包含を通じてそのような切断を定める。
テンプレート:Mvar を テンプレート:Mvar 上のベクトル場、すなわち テンプレート:Mvar の切断とするとき、微分を点ごとにテンプレート:Mvar に適用することにより、ベクトル場の押し出し テンプレート:Math が誘導され、これは テンプレート:Mvar に沿うベクトル場、すなわち テンプレート:Mvar 上の テンプレート:Math の切断である。
テンプレート:Mvar 上の任意のベクトル場 テンプレート:Mvar は テンプレート:Math のテンプレート:仮リンク テンプレート:Math を テンプレート:Math なるものとして定義する。テンプレート:Mvar 上のベクトル場 テンプレート:Mvar と テンプレート:Mvar 上のベクトル場 テンプレート:Mvar が テンプレート:Mvar-関係を持つ (テンプレート:Mvar-related) とは、テンプレート:Mvar に沿うベクトル場として テンプレート:Math を満たすとき、すなわち各点 テンプレート:Math に対し テンプレート:Math が成り立つときに言う。
条件によっては、与えられた テンプレート:Mvar 上のベクトル場 テンプレート:Mvar に対して テンプレート:Mvar と テンプレート:Mvar-関係を持つ テンプレート:Mvar 上のベクトル場 テンプレート:Mvar が一意に決まるということもあり得る。特に テンプレート:Mvar が微分同相写像であるときには必ずそうなる。この場合、押出しが定める テンプレート:Mvar 上のベクトル場 テンプレート:Mvar は テンプレート:Math で与えられる。
より一般の状況として、テンプレート:Mvar が全射のとき(例えば、ファイバー束の束射影のとき)、テンプレート:Mvar 上のベクトル場 テンプレート:Mvar が射影可能 (projectable) とは、任意の テンプレート:Math に対して テンプレート:Math が テンプレート:Math の取り方に依らないときに言う。この条件はちょうど、テンプレート:Mvar の押し出しが テンプレート:Mvar 上のベクトル場として定義可能となることを保証するものになっている。
関連項目
参考文献
- John M. Lee, Introduction to Smooth Manifolds, (2003) Springer Graduate Texts in Mathematics 218.
- Jürgen Jost, Riemannian Geometry and Geometric Analysis, (2002) Springer-Verlag, Berlin ISBN 3-540-42627-2 See section 1.6.
- Ralph Abraham and Jerrold E. Marsden, Foundations of Mechanics, (1978) Benjamin-Cummings, London ISBN 0-8053-0102-X See section 1.7 and 2.3.