双曲線

双曲線

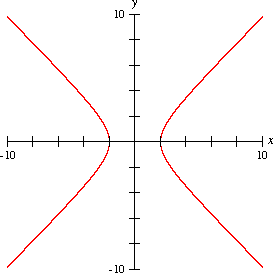
双曲線（そうきょくせん、テンプレート:Lang-en-short）とは、2次元ユークリッド空間 ℝ² 上で定義され、ある2点 F, F' からの距離の「差が一定」であるような曲線の総称である。

この2点 F, F' は焦点と呼ばれる。2点 F, F' を通る直線と2点 F, F' の垂直二等分線は主軸と呼ばれる。

双曲線の方程式

一般形

2次元直交座標系において、双曲線の2焦点の座標をそれぞれ $(a,b)$, $(c,d)$、焦点からの距離の差の絶対値を $k$ とする。このとき双曲線の方程式は、次のように表される。これを一般形という。

$|\sqrt{(x-a{)}^2+(y-b{)}^2}-\sqrt{(x-c{)}^2+(y-d{)}^2}|=k$

この方程式は、うまく式変形することにより、必ず

$A{x}^2+Bxy+C{y}^2+Dx+Ey+F=0$　　（ただし $A,B,C,D,E,F$ は実数）

という形に表すことができる。証明は以下の通り。

標準形

双曲線の標準形

標準形	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$
漸近線	$\frac{x}{a}\pm \frac{y}{b}=0$	$\frac{x}{a}\pm \frac{y}{b}=0$
焦点	$(\pm \sqrt{a^2+b^2},0)$	$(0,\pm \sqrt{a^2+b^2})$
頂点	$(\pm a,0)$	$(0,\pm b)$
準線	$x=\pm \frac{a^2}{\sqrt{a^2+b^2}}$	$y=\pm \frac{b^2}{\sqrt{a^2+b^2}}$
離心率	$e=\frac{\sqrt{a^2+b^2}}{a}$	$e=\frac{\sqrt{a^2+b^2}}{b}$

双曲線は、主軸を座標軸とする直角座標系において、次の方程式により表すことができる。これを標準形という。

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ テンプレート:Vanc

この場合、焦点の座標は

$F(-\sqrt{a^2+b^2},0),F^{\prime }(+\sqrt{a^2+b^2},0)$

と書ける。このとき、2焦点 F, F' から双曲線上の点 P への距離の差 |PF − PF'| は 2テンプレート:Mvar となる。原点を双曲線の中心といい、2点(±テンプレート:Mvar, 0) を双曲線の頂点という。

双曲線上の点 P と焦点 F との距離 PF と点 P から準線 $x=\frac{a^2}{\sqrt{a^2+b^2}}$ までの距離の比は一定であり、比の値は離心率 $e=\frac{\sqrt{a^2+b^2}}{a}$ に等しい。

また、双曲線には2つの漸近線が存在しており、漸近線の方程式は

$\frac{x}{a}+\frac{y}{b}=0,\frac{x}{a}-\frac{y}{b}=0$

である。

特に、漸近線が直交している、すなわち テンプレート:Mvar = テンプレート:Mvar であるとき、この双曲線を特に直角双曲線という。

反比例のグラフ テンプレート:Math も双曲線の一種である。これは、直角双曲線：テンプレート:Math を原点の回りに テンプレート:Math だけ回転させた双曲線に等しい。

媒介変数表示

双曲線は、双曲線関数を用いて媒介変数表示することができる。

$\{\begin{array}{c}x=\pm a\cosh t\\ y=b\sinh t\end{array}$

また双曲線から左側の頂点 テンプレート:Math を除けば有理関数を用いて媒介変数表示することもできる。

$\{\begin{array}{c}x=a\frac{1+t^2}{1-t^2}\\ y=b\frac{2t}{1-t^2}\end{array}$

ただし テンプレート:Math とする。右側の連結成分は テンプレート:Math に、左下の連結成分は テンプレート:Math に、左上の連結成分は テンプレート:Math に対応する。これは二点 テンプレート:Math と テンプレート:Math を通る直線 テンプレート:Math と双曲線との交点のひとつとして得られる。

円錐曲線としての双曲線

円錐切断面の4つのタイプ (放物線、楕円、円、双曲線)

双曲線は、直円錐を直円錐の頂点を通らず、上下両方の直円錐に交わる平面で切断したときの、切断面の境界である。

離心率が テンプレート:Mvar であるような円錐曲線を C_{テンプレート:Mvar} とする。このとき、テンプレート:Mvar ＞ 1 であれば、 C_{テンプレート:Mvar} は双曲線となる。この円錐曲線を適当に直交変換することにより、準線が テンプレート:Mvar = −テンプレート:Mvar , 焦点の一つが F(テンプレート:Mvar, 0) となったとする。双曲線の任意の点 P(テンプレート:Mvar, テンプレート:Mvar) に対し、方程式

$e(x-f)=\mathrm{P}\mathrm{F}$

が成立するが、$\mathrm{P}\mathrm{F}=\sqrt{(x-f{)}^2+y^2}$ となるから、上方程式の両辺を2乗して移項整理することにより、

$x^2+2\left(\frac{e^2+1}{e^2-1}\right)fx-\frac{y^2}{e^2-1}=-f^2$

さらに テンプレート:Mvar に関して平方完成させることにより、

${(x+\left(\frac{e^2+1}{e^2-1}\right)f)}^2-\frac{y^2}{e^2-1}={\left(\frac{2e}{e^2-1}f\right)}^2$

これが、円錐曲線としての双曲線の基本形である。さらに平行移動：$X=x+\frac{e^2+1}{e^2-1}f$ , Y = テンプレート:Mvar を行って適当に整理することによって、(*) の形になる。

参考文献

• テンプレート:Cite book
• テンプレート:Cite book

関連項目

• 円錐曲線 - 楕円 - 放物線
• 彗星
• 双曲面
• 天体力学
• レムニスケート

外部リンク

• テンプレート:Kotobank
• テンプレート:高校数学の美しい物語
• 双曲線の定義・標準形・焦点・漸近線、双曲線の方程式の決定
• 双曲線の知識まとめ（焦点・漸近線・方程式・媒介変数表示・接線公式）
• 双曲線の方程式
• デカルトの双曲線作図器１
• テンプレート:MathWorld