一次関数
テンプレート:About テンプレート:出典の明記 数学、特に初等解析学における(狭義の)一次関数(いちじかんすう、テンプレート:Lang-en-short)は、(テンプレート:仮リンクの)一次多項式関数(テンプレート:En)、つまり次数 テンプレート:Math の多項式が定める関数
をいう(もしくは と表記される)。ここで、係数 テンプレート:Math2 は テンプレート:Mvar に依存しない定数であり、矢印は各値 テンプレート:Mvar に対して テンプレート:Math2 を対応させる関数であることを意味する。特に解析幾何学において、係数および定義域は実数の範囲で扱われ、その場合一次関数のグラフは平面直線である。 より広義には、係数や定義域として複素数やその他の環を考えたり、多変数の一次多項式関数や、あるいは一次式をベクトル空間や作用を持つ加群の文脈で理解することもある。

一次関数は線型関数(テンプレート:En)やアフィン関数(テンプレート:En)とも呼ばれ、この場合しばしば定数関数 (テンプレート:Math2) も含む。ベクトルを変数とする広義の一次関数はアフィン写像と呼ばれ、これはベクトルにベクトルを対応させる写像であるが、ふつう線型写像はその特別な場合 (テンプレート:Math2) で斉一次関数で与えられる。
以下、解析幾何学における実関数としての一次関数について述べる。
定義と簡単な説明
初等解析学において、不定元 テンプレート:Mvar に関する高々一次の多項式 テンプレート:Math(テンプレート:Math は実定数)に対し、テンプレート:Mvar を実変数とみて得られる写像
を一次関数と呼ぶ(見かけ上一次なだけでなく実際に「一次」であることを要請する場合は「テンプレート:Math」とする)。定数関数となる テンプレート:Math を含める場合は、これを「退化」しているといい、そうでない場合を非退化という。
解析幾何学において、デカルト座標が与えられたテンプレート:Mvar-平面 テンプレート:Math 上に、一次関数 テンプレート:Math のグラフ
は直線を描くため、一次関数は「直線の式」(あるいは単に「直線」)としても知られ、言葉の濫用で(一次函数それ自身とそのグラフとをとくに区別することなく扱って)直線 テンプレート:Math などともいう。

一次式 テンプレート:Math を特徴付けるふたつの定数について、テンプレート:Mvar が増減すると対応する直線の「傾き」が急になったり緩やかになったりするので、テンプレート:Mvar はこの直線の傾きと呼ばれる。また テンプレート:Mvar は対応する直線と テンプレート:Mvar-軸との交点の座標であり テンプレート:Mvar-切片 (テンプレート:Mvar-intercept) あるいは単に切片と呼ばれる。また、テンプレート:Mvarは変化の割合(変化率)とも呼ばれ、変化の割合はテンプレート:Sfracで求められる[1]。
- 傾き テンプレート:Mvar が正の場合はグラフは右上がりになり、負の場合は右下がりになる。いずれの場合も、テンプレート:Mvar の絶対値が大きくなるほど傾きが「急」になる。
- テンプレート:Mvar-切片 テンプレート:Mvar が増減すると対応する直線は座標平面を上下に平行移動する。
テンプレート:Mvar-切片(直線と テンプレート:Mvar-軸の交点)は テンプレート:Math の零点 テンプレート:Math であたえられる。
一次関数 テンプレート:Mvar が非退化 (テンプレート:Math) ならば、非有界、非周期的、かつ単調増大 (テンプレート:Math) または単調減少 (テンプレート:Math) である。さらに単射かつ全射、従って一対一対応ゆえに可逆(であって、逆関数もまた非退化な一次関数)である。これと対照に、定数関数に退化している (テンプレート:Math) ならば、有界、周期的、かつ偶関数であり、非増大かつ非減少の意味では単調であるが、単射でも全射でもなく(したがって一対一対応にならず)逆函数を持たない。退化・非退化の場合によらず テンプレート:Math のとき一次関数は奇関数であり、偶かつ奇となるのは定数関数 テンプレート:Math に限る。


平面直線の式として
傾き・切片標準形
一次関数の表す直線の式 テンプレート:Math は、傾きと テンプレート:Mvar-切片を与えることによって一意的に決定される「傾き・切片(標準)形」(slope-intercept form) であり、座標平面上で直線を表す式としては他に「点・傾き(標準)形」(point-slope form) である
(点 テンプレート:Math を通る、ただ一つの傾き テンプレート:Mvar の直線)や「一般形」(general form)
(これ自体は二変数の一次方程式である)が挙げられる。詳細は平面における直線の標準形も参照。 一般形は平面上のあらゆる直線を表すだけの能力を持ち、これには テンプレート:Mvar-軸に垂直(テンプレート:Mvar-軸に平行)な直線 テンプレート:Math なども含まれるが、この種の直線の傾きは定まらないため傾きを明示的に利用する標準形では表せないし、一次関数どころか関数でさえない。また、テンプレート:Mvar-軸に平行な傾き テンプレート:Math の直線は、定数関数に対応しているのであり、一次関数 テンプレート:Math の定義に テンプレート:Math を仮定するならば、これも一次関数では表せないことになる。 テンプレート:-
二点標準形

一次関数の傾きは通る二点が分かれば一意的に決定できるので、一次関数はそれが通る二点が決まればただひとつに決まる。一次関数 テンプレート:Math が二点 テンプレート:Math を通るとき、テンプレート:Math =テンプレート:Sfrac は点の取り方に依らず一定で、傾きに等しく
が成り立つ。この直線は点 テンプレート:Math を通る(あるいは点 テンプレート:Math を通る)のだから点・傾き標準形と合わせて考えれば、二点標準形が得られ、この一次関数は
と書くことができる。
直線の成す角の正接と傾き
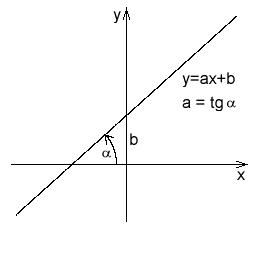
直線 テンプレート:Math が テンプレート:Mvar-軸の正の向きと成す角(方向角)が テンプレート:Mvar であるとすると、この直線の傾きは正接関数を用いて
と書くことができる。この意味で、傾き テンプレート:Mvar は直線の方向を決める方向ベクトルを与えている。さらに別の直線 テンプレート:Math が テンプレート:Mvar-軸の正の向きと成す角が テンプレート:Mvar であるとすれば、この二つの直線の成す角 テンプレート:Math は
から求まる。とくに角 テンプレート:Math が直角 テンプレート:Math であるとき、この式は
の形に書けるから、一次関数が表す直線の直交条件を「傾きの積が テンプレート:Math に等しい」と述べることもできる。 テンプレート:-
解析学
一次函数は(任意の多項式函数がそうであるように)連続かつ微分可能(とくになめらか)である。一次関数 テンプレート:Math の導関数は
という定数関数で、それより高階の導函数は常に テンプレート:Math となる。特に傾き テンプレート:Mvar が テンプレート:Math として求められる。テンプレート:Math であるから、この一次関数を
の形に書けば、これは一次関数のテイラー展開に他ならない。また展開の中心を テンプレート:Math に変更すれば
となるが、これは上で通る二点 テンプレート:Math から定まる式として述べたものの、一方を他方に近づけた極限に等しい。あるいはこれは一次函数に関する平均値の定理を述べたものと看做すこともできる。
また テンプレート:Mvar の原始関数の一つは
で与えられる。
一次関数の演算
係数は適当な体、あるいは整域 テンプレート:Math にとるものとする。ふたつの一次関数 テンプレート:Math に対して、それらの和 テンプレート:Math を点ごとの値の和
によって定めると、これは再び一次関数を与える。一次関数の全体は可換群を成すことを確かめるのは容易である。また、定数倍 テンプレート:Mvar を
で与えれば、一次関数の全体が テンプレート:Math と テンプレート:Mvar の張る二次元のベクトル空間となることがわかる。一方、点ごとの積
は(テンプレート:Mvar か テンプレート:Mvar の何れかが定数関数でないかぎり)もはや一次関数ではないテンプレート:Efnが、合成
は再び一次関数である。とくに テンプレート:Math ならば一次関数 テンプレート:Math は テンプレート:Mvar の逆函数になる。
一般化
テンプレート:Main 多変数の一次多項式が定める関数
も一次関数という。テンプレート:Math のときは斉一次函数あるいは一次形式 (linear form) という。この関数のグラフ
は、テンプレート:Math-次元ユークリッド空間 テンプレート:Math において超平面(テンプレート:仮リンク テンプレート:Math のアフィン部分空間)を描く。このような関数に対しても、上に述べたことは(平面における各概念の高次元における適当な対応物を考えることにより)ほとんどそのままの形で通用する。
より一般に、テンプレート:Mvar 次元ベクトル空間 テンプレート:Mvarテンプレート:Mvar から テンプレート:Mvar 次元ベクトル空間 テンプレート:Mvarテンプレート:Mvar への一次関数を考えることもできる。テンプレート:Mvar を テンプレート:Mvar-次元ベクトル値の変数、テンプレート:Mvar を テンプレート:Mvar-次元の定ベクトル、テンプレート:Mvar を テンプレート:Mvar-行 テンプレート:Mvar-列の行列とするとき、
をアフィン写像という。特に、テンプレート:Mvar = 0 のときかつそのときに限り、和とスカラー倍を保つ線型写像となる。
実数全体の成す体 テンプレート:Mvar を任意の可換環 テンプレート:Mvar で置き換えて
を考えることもできるし、行列環 テンプレート:Mvarテンプレート:Mvar やその部分環、あるいは一般線型群 テンプレート:Mvarテンプレート:Mvar やその部分群を、一般の環 テンプレート:Mvar や群 テンプレート:Mvar で置き換え、ベクトル空間 テンプレート:Mvar をそれらの環や群が作用する加群 テンプレート:Mvar で置き換えれば、
のようなものを考えることもできる。このようなものはアフィン群あるいは俗に テンプレート:Mvar + テンプレート:Mvar 群と呼ばれ、この群の上の調和解析は、ウェーブレット解析として知られる。