ピカールの逐次近似法

解析学において、ピカールの逐次近似法（ピカールのちくじきんじほう、テンプレート:Lang-en-short）とは、常微分方程式の初期値問題に対し、解に一様収束する関数列を構成する手法テンプレート:Sfnpテンプレート:Sfnpテンプレート:Sfnpテンプレート:Sfnp。常微分方程式の初期値問題と同値な積分方程式に基づき、関数列を逐次的に構成する。常微分方程式の解の存在と一意性に関する基礎定理の証明に用いられる。より一般的な距離空間論の観点からは、この逐次近似列の構成法は縮小写像に対応しており、逐次近似法で得られる解は反復合成写像の不動点として捉えられるテンプレート:Sfnpテンプレート:Sfnp。ピカールの逐次近似法という名は19世紀のフランスの数学者エミール・ピカールに因む。ピカールは逐次近似の手法を発展させ、現在、常微分方程式の解の存在と一意性の理論で一般的に用いられる証明の論法を確立させた。

導入

テンプレート:Mvar を実数空間 テンプレート:Math に値をとる独立変数、テンプレート:Math を テンプレート:Mvar-次実数空間 テンプレート:Math（または テンプレート:Math）に値をとるベクトル値の未知関数を表すものとする。テンプレート:Mvar を テンプレート:Math（または テンプレート:Math）の領域とし、テンプレート:Math を テンプレート:Mvar 上で定義された テンプレート:Math（または テンプレート:Math）に値をとる連続関数とする。このとき、正規形の1階常微分方程式

$\frac{d}{dt}𝒙(t)=𝒇(t,𝒙(t))$

において、テンプレート:Mvar 内の点 テンプレート:Math に対し、初期条件

$𝒙(\tau )=\mathit{\xi }$

を満たす解 テンプレート:Math を テンプレート:Mvar を含む区間 テンプレート:Mvar で求める初期値問題を考える。この初期値問題を解くことは積分方程式

$𝒙(t)=\mathit{\xi }+\underset{\tau }{\overset{t}{\int }}𝒇(s,𝒙(s))ds$

を解くことと同値である。

内容

ピカールの逐次近似法の例。非自励系の初期値問題 テンプレート:Math, テンプレート:Math に対し、青線が解、オレンジ線がピカールの逐次近似法で構成される関数列 テンプレート:Mathである。ここで、テンプレート:Math, テンプレート:Math, テンプレート:Math2 である。

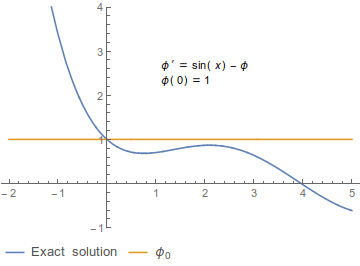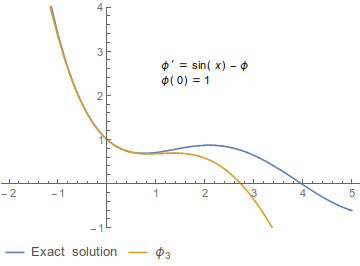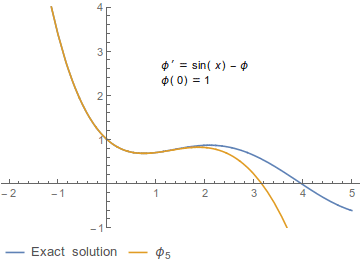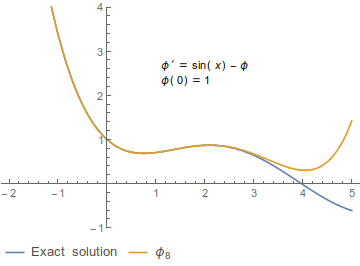
ピカールの逐次近似法では初期値問題と同値な積分方程式を基づき、次のように初期条件から逐次的に関数列 テンプレート:Math を構成する。

$\begin{array}{cc}{\mathit{\phi }}_0(t)& =\mathit{\xi },\\ {\mathit{\phi }}_n(t)& =\mathit{\xi }+\underset{\tau }{\overset{t}{\int }}𝒇(s,{\mathit{\phi }}_{n-1}(s))ds(n=1,2,\cdots ).\end{array}$

このとき、極限関数

$\mathit{\phi }(t)=\underset{n\to \mathrm{\infty }}{\lim }{\mathit{\phi }}_n(t)$

が存在すれば、これは上述の常微分方程式の初期値問題と同値な積分方程式を満たすことが期待される。

但し、この逐次近似法で構成する関数列 テンプレート:Math が適切に定義され、その存在と収束が保証される必要がある。そのために次の条件を要請する。

テンプレート:Math（または テンプレート:Math）の有界閉領域

$E=\{(t,𝒙):|t-\tau |\le r,\Vert 𝒙-\mathit{\xi }\Vert \le \rho \}$

で テンプレート:Math は連続で有界、すなわちある テンプレート:Mvar が存在して

$\Vert 𝒇(t,𝒙)\Vert \le M$

かつ、 テンプレート:Math についてのリプシッツ条件

$\Vert 𝒇(t,𝒙)-𝒇(t,𝒚)\Vert \le L\Vert 𝒙-𝒚\Vert$

を満たすとする。このとき、

$r_0:=\min (r,\rho /M)$

で定まる区間

$I_0=\{t\in ℝ:|t-\tau |\le r_0\}$

で テンプレート:Math は

$\Vert {\mathit{\phi }}_n(t)-\mathit{\xi }\Vert \le \rho$

を満たす連続関数として、適切に定義され、極限関数 テンプレート:Math に一様収束する。テンプレート:Math の定義と テンプレート:Math の連続性より、テンプレート:Math は

$\mathit{\phi }(t)=\mathit{\xi }+\underset{\tau }{\overset{t}{\int }}𝒇(s,\mathit{\phi }(s))ds$

を満たし、所与の常微分方程式の初期値問題の解である。

縮小写像の不動点定理

積分作用素 テンプレート:Mvar を

$T\mathit{\varphi }=\mathit{\xi }+\underset{\tau }{\overset{t}{\int }}𝒇(s,\mathit{\varphi }(s))ds$

で定めると、上述の積分方程式の解は、

$T\mathit{\varphi }=\mathit{\varphi }$

を満たす テンプレート:Mvar の不動点である。ピカールの逐次近似法では、関数列 テンプレート:Math は テンプレート:Mvar の反復合成

$T{\mathit{\phi }}_n={\mathit{\phi }}_{n-1}$

で構成されるが、一定の条件の下では テンプレート:Mvar は縮小写像となり、不動点定理からも解の存在が保証されるテンプレート:Sfnpテンプレート:Sfnp。 実際、先ほどと同様に、テンプレート:Math は有界閉領域 テンプレート:Mvar で連続かつリプシッツ連続であるとする。ここで

$0<L{r_0}^{\prime }<1,{r_0}^{\prime }\le r_0$

を満たす正の定数 テンプレート:Math で定まる閉区間

${I_0}^{\prime }=\{t\in ℝ:|t-\tau |\le {r_0}^{\prime }\}$

をとる。テンプレート:Math 上で定義される テンプレート:Math（または テンプレート:Math）に値をとる連続関数のなすベクトル空間を $𝒞$ とし、$𝒞$ にノルムを

$\Vert \mathit{\varphi }{\Vert }_{{I_0}^{\prime }}=\underset{t\in {I_0}^{\prime }}{\max }\Vert \mathit{\varphi }(t)\Vert$

で定めると、$𝒞$ は完備なノルム空間となる。$𝒞$ の部分集合で条件

$\Vert \mathit{\varphi }(t)-\mathit{\xi }\Vert \le \rho$

を満たすものからなる $ℱ$ は完備な閉部分集合であり、テンプレート:Mvar は $ℱ$ から $ℱ$ への

$\Vert T\mathit{\varphi }-T\mathit{\psi }{\Vert }_{{I_0}^{\prime }}\le L{r_0}^{\prime }\Vert \mathit{\varphi }-\mathit{\psi }{\Vert }_{{I_0}^{\prime }}(\mathit{\varphi },\mathit{\psi }\in ℱ)$

を満たす縮小写像である。よって、バナッハの不動点定理により、テンプレート:Math を満たす $ℱ$ の不動点、すなわち区間 テンプレート:Math 上で定義される初期値問題の解 テンプレート:Math が存在する。

例

例1

次の自励系のスカラー微分方程式の初期値問題を考えるテンプレート:Sfnp。

$\frac{dx(t)}{dt}=x(t),x(0)=1.$

ピカールの逐次近似法で テンプレート:Math を構成すると

$\begin{array}{cc}{\phi }_1(t)& =1+\underset{0}{\overset{t}{\int }}1ds=1+t,\\ {\phi }_2(t)& =1+\underset{0}{\overset{t}{\int }}(1+s)ds=1+t+\frac{t^2}{2},\\ & ⋮\\ {\phi }_n(t)& =1+t+\frac{t^2}{2}+\cdots +\frac{t^n}{n!}=\sum _{l=0}^n\frac{t^l}{l!}.\end{array}$

よって、解は

$\phi (t)=\underset{n\to \mathrm{\infty }}{\lim }{\phi }_n(t)=e^t$

となる。

例2

次のスカラー微分方程式の初期値問題を考えるテンプレート:Sfnp。

$\frac{dx(t)}{dt}=tx(t),x(0)=1$

ピカールの逐次近似法で テンプレート:Math を構成すると

$\begin{array}{cc}{\phi }_1(t)& =1+\underset{0}{\overset{t}{\int }}sds=1+\frac{t^2}{2}\\ {\phi }_2(t)& =1+\underset{0}{\overset{t}{\int }}s(1+\frac{s^2}{2})ds=1+\frac{t^2}{2}+\frac{t^4}{2\cdot 4}\\ & \cdots \\ {\phi }_n(t)& =1+\frac{t^2}{2}+\frac{t^4}{2\cdot 4}+\cdots +\frac{t^{2n}}{2\cdot 4\cdots \cdot (2n)}=\sum _{l=0}^n\frac{1}{l!}{\left(\frac{t^2}{2}\right)}^l\end{array}$

よって、解は

$\phi (t)=\underset{n\to \mathrm{\infty }}{\lim }{\phi }_n(t)=e^{t^2/2}$

となる。

リプシッツ条件についての注意

リプシッツ条件が満たされない場合、逐次近似列 テンプレート:Math が定義されても、その収束は保証されない。そのような場合として、次の例を考えるテンプレート:Sfnp。

$D=\{(t,x)\in {ℝ}^2:-\mathrm{\infty }<t<1,-\mathrm{\infty }<x<\mathrm{\infty }\}$

とし、テンプレート:Math を

$f(t,x)=\{\begin{array}{cc}0& (-\mathrm{\infty }<t\le 0,x\in ℝ)\\ 2t& (0<t\le 1,-\mathrm{\infty }<x<0)\\ 2t-\frac{4x}{t}& (0<t\le 1,0\le x\le t^2)\\ -2t& (0<t\le 1,t^2<x<\mathrm{\infty })\end{array}$

で定義すると、テンプレート:Mvar 上で テンプレート:Math は連続かつ

$|f(t,x)|\le 2((t,x)\in D)$

で有界であるが、リプシッツ連続ではない。このとき、初期値問題

$\frac{dx(t)}{dt}=f(t,x),x(0)=0$

を考えると、逐次近似列は

${\phi }_{2k-1}(t)=t^2,{\phi }_{2k}(t)=-t^2(k=1,2,\cdots )$

となり、収束しない。一方で、解は

$\phi (t)=\frac{t^3}{3}$

である。

参考文献

• テンプレート:Cite book
• テンプレート:Cite book
• テンプレート:Cite book
• テンプレート:Cite book
• テンプレート:Cite book
• テンプレート:Cite book

関連項目

• ピカール＝リンデレーフの定理
• 反復合成写像
• バナッハの不動点定理