ブレイド群
数学においてブレイド群(braid group、組みひも群とも呼ぶ)とは、直観的には平行に張られた複数の紐(braid)において、その隣り合う紐を交差させる操作を生成元とし、常に同じ絡まり方を生じる異なる交差操作の等式を関係式とする群である。特に紐がテンプレート:Mvar本のときこの群をテンプレート:Mathと書く。
ブレイド群は1925年にエミール・アルティンにより初めて明確に定義された。しかしそれ以前に配置空間の基本群として、1891年のアドルフ・フルヴィッツのモノドロミーの論文において暗に現れており[1]、更に遡ってガウスもアルティンと同様の着想を得ていたとも考えられている。
定義
特殊なnの場合
以下n=4とする。
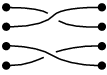
一列に並んだ4点が二組あり、それらの間を結ぶ平行な紐が4本ある下図(以下eにより参照)のような状況を考える。
 |
これらの紐に対し隣同士の紐を交差させる以下の3つの操作を考える。
 |
 |
 |
これらの紐の交差においては上下を区別しており、例えば以下はとは異なる操作と看做される(これは後述の積の定義によりの逆元であると看做せる)。

|
及び、その交差の上下を逆にした操作を繰り返して得られる一つの具体的な紐の状態をブレイド又は組紐と呼ぶ(以下上図の自身もブレイドとも看做すこととする)。
二つのブレイドa, bがあるとき、aの右にbを繋げaの元の左の端点とbの右の端点を新たな端点とするブレイドを、aとbの積abと定義する。 以下に例を示す。
| a | b | ab | |
|---|---|---|---|
| 例1 |  |
 |
 |
| 例2 |  |
 |
 |
任意のブレイドと、冒頭のブレイドの積は元のブレイドを変えない(即ちは単位元)。 また任意のブレイドに対し、その右端の全点を通る縦線を軸として鏡映反転させたブレイドとの積を取るととなるため、常に逆元が存在することがわかる。 従ってブレイドは上記の積に関して群となり、この群がである。 定義よりの任意のブレイドを及び、その逆元の積として表現することができる。
をを生成元とする群とみたとき、その基本関係式は下記1~3と定められる。これらは本質的に同じ絡まり方を表すブレイドに関する等式であり、1は対象に共通の紐がない交差操作は可換であることを示す条件で、2及び3はライデマイスター移動III型の同値性に相当する。

一般のnの場合
この例を テンプレート:Math 本の紐へ一般化して、群 テンプレート:Mathは次の表示により定義される。テンプレート:Refnest
ここに、最初の等式ではテンプレート:Math であり、第二の等式ではテンプレート:Mathである。 テンプレート:Refnest これらの関係式はブレイド関係式(braid relations)と呼ばれている。テンプレート:Refnest
基本的性質
- テンプレート:Math は自明な群、テンプレート:Math は無限巡回群 テンプレート:Math であり、テンプレート:Math は三葉結び目の結び目群と同型である。
- テンプレート:Math に対し、テンプレート:Math は 2つの生成元を持つ自由群と同型な部分群を含む。従ってこれらの群は非可群な無限群である。
- 単位元を除くすべての テンプレート:Math の元は、その位数が無限である。即ち、テンプレート:Math は捩れを持たない。
- テンプレート:Math 上には、テンプレート:仮リンクと呼ばれる左不変な全順序が存在する。
ブレイドの解釈
結び目としての解釈
テンプレート:Main ブレイドの両端をつなげることにより一つの結び目又は絡み目が得られる。 逆に、すべての結び目と絡み目は少なくとも一つのブレイドとして表現可能であることが知られている(アレクサンダーの定理)。 ブレイドは生成子 テンプレート:Mathに関する語(word)として与えられるため、計算機プログラムで結び目を扱う方法として採用されている。
写像類群とブレイドの分類への関係
ブレイド群 テンプレート:Math は、テンプレート:Math 個の穴を有する円板のテンプレート:仮リンク(mapping class group)と同型であることを示すことができる。これは直感的には、写像類群の各元が穴同士を入れ替えるので、元の作用前後の同じ位置にある穴を繋ぐ紐の集合をブレイドと看做すことでブレイドと対応させることができることによる。
写像類群の元に関するテンプレート:仮リンク(Nielsen-Thurston classification)によって、ブレイドを周期的、可約、擬アノソフの3種類に分類することができる。
ブレイド群の作用
置換による対称群の作用と類似して、様々な数学的設定におけるテンプレート:Math個の対象の組やテンプレート:Math重のテンソル積に対して、ブレイド群は以下の自然な作用を有する。
テンプレート:Math を任意の群、テンプレート:Math を テンプレート:Math の元のすべての テンプレート:Math個の組の集合で、それらの積が テンプレート:Math の単位元となる集合とすると、に対する以下の写像はテンプレート:Math の上へのテンプレート:Mathの作用である。
この対応は、成分テンプレート:Math と テンプレート:Math の位置を交換し、更にテンプレート:Mathをテンプレート:Mathに関する内部自己同型を付加しただけであるため、作用後の元の成分の積が再び単位元であることが保証される。また、これがブレイド群の関係式を満たすことも確認できる。
別な例として、ブレイド群の作用を持つモノイダル圏としてテンプレート:仮リンク(braided monoidal category)が考えられている。そのような構造は、現代の数理物理学で重要な役目を果し、量子結び目不変量を導く。
ブレイド群の表現
ブレイド群 テンプレート:Math の線形表現として古典的なテンプレート:仮リンクや、テンプレート:仮リンクが知られている。テンプレート:Refnest
Burau表現は、1変数の整係数ローラン多項式環の一般線形群への表現と看做せる:
Burau表現が忠実であるか否かは長い間問題となっていたが、テンプレート:Math に対しては否定的であることが判明した。
Lawrence-Krammer(-Bigelow)表現は、2変数の整係数ローラン多項式環の一般線形群への表現と看做せる:
2001年頃Stephen BigelowとDaan Krammerが独立に、この表現を用いてすべてのブレイド群が線型であることを証明した。
1996年、C. Nayakとフランツ・ウィルチェック(Frank Wilczek)は、テンプレート:Mathの射影表現の類似として、ブレイド群の射影表現が分数量子ホール効果における準粒子に関する物理的意味を有することを提唱した[2]。
その他
計算関係
ブレイドには生成元テンプレート:Mathによる正規化表現が存在し、ブレイドのテンプレート:仮リンク(word problem)を効率的に処理することができる。 実際数式処理システムには、生成元で与えられたブレイドに対してこの問題を解くことができるものがある。テンプレート:Refnest 語の問題は、テンプレート:仮リンク(Lawrence-Krammer representation)を通しても効率的に解くことができる。
その他、ブレイド群に関する計算論的に難しい問題があるため、暗号理論への応用が提案されている。[3]
テンプレート:Math とモジュラー群の関係
ブレイド群 B3は、モジュラー群の中心拡大(central extension)である。即ち、の中心をにより表すとき以下の短完全列を満たす:
従ってである。
関連する群
純粋ブレイド群
ブレイドの紐の交差の上下を無視すると、テンプレート:Math 本の紐のブレイドは テンプレート:Math 個の元の置換を定める。実際ブレイド の像を隣接互換 テンプレート:Math とする写像は、ブレイド群から対称群への全射群準同型 テンプレート:Math である。 この準同型 テンプレート:Math の核を純粋ブレイド群(pure braid group)と呼び、テンプレート:Math と書く。即ち純粋ブレイド群は以下の短完全列を満たすものである。
純粋ブレイド群は、その元が単位置換に写像されるものであるため、幾何学的には各々の紐において起点と終点が必ず同じ位置にあるブレイドの全体と解釈することができる。
また純粋ブレイド群は、以下の分裂する短完全系列を満たすため、一般論から自由群の半直積を繰り返し取ったものと看做すこともできる。
関連事項
- 組みひも理論
- テンプレート:仮リンク(Non-commutative cryptography)
脚注
注釈
出典
- ↑ テンプレート:Cite book
- ↑ テンプレート:Citation Some of Wilczek-Nayak's proposals subtly violate known physics; see the discussion テンプレート:Citation
- ↑ テンプレート:Cite arXiv
さらに先の書籍
外部リンク
- テンプレート:Planetmath reference
- CRAG: CRyptography and Groups at Algebraic Cryptography Center Contains extensive library for computations with Braid Groups
- テンプレート:SpringerEOM
- Stephen Bigelow's exploration of B5 Java applet.
- テンプレート:Citation
- Braid group: List of Authority Articles on arxiv.org.