全射

テンプレート:参照方法 数学において、写像が全射的（ぜんしゃてき、テンプレート:Lang-en-short）であるとは、その終域となる集合の元はどれもその写像の像として得られることを言う。即ち、集合 テンプレート:Mvar から集合 テンプレート:Mvar への写像 テンプレート:Mvar について、テンプレート:Mvar の各元 テンプレート:Mvar に対し テンプレート:Math となるような テンプレート:Mvar の元 テンプレート:Mvar が（一般には複数あってもよいが）対応させられるとき、写像 テンプレート:Mvar は全射 テンプレート:Lang であるという。全写（あるいは全写像）とも書く。

域 X（赤）から余域 Y（青+黄）への写像 f の模式図（余域 Y の内側の小さい楕円（黄）は f の値域）。これは一般には全射を表していない（一つも青に塗られる点がないときのみ全射）。

全射（および単射、双射）の語は20世紀フランスの数学結社ブルバキ（1935年以降『数学原論』シリーズを刊行している）により導入されたものである。接頭辞 テンプレート:Lang はフランス語で「上の」を意味し、写像の始域が終域全体をすっぽり覆い尽くすように写し込まれるイメージを反映したものになっている。sur, in, bi, jection いずれもラテン語源である。

定義

写像 テンプレート:Math について、テンプレート:Mvar の値域 テンプレート:Math が終域（余域）テンプレート:Mvar を含む（つまり テンプレート:Math）ならば、写像 テンプレート:Math は 全射 (surjection) であるという。テンプレート:Mvar は余域 テンプレート:Mvar への全射的 (surjective) な写像である、テンプレート:Mvar の上への (onto) 写像であるなどともいうテンプレート:Efn。記号で書けば、テンプレート:Math が全射であるとは テンプレート:Math を満足することである。このとき、しばしば鏃が二つの矢印を使って $f:A\twoheadrightarrow B$ と表す。

• 
  全射であり単射でない
• 
  単射であり全射でない
• 
  全単射
• 
  全射でも単射でもない

例

• 実数 テンプレート:Mvar に対し、その自乗 テンプレート:Math を対応させる非負実数値写像 $f:ℝ\ni x\mapsto x^2\in {ℝ}_{+}$ は全射である。ただし テンプレート:Math で非負実数全体の集合を表している。実際、テンプレート:Math に対し、その非負平方根 テンプレート:Math をとれば、テンプレート:Math とすることができる（負の平方根 テンプレート:Math をとっても構わない）。終域を変更して、単に実関数 $f:ℝ\ni x\mapsto x^2\in ℝ$ と考えたのでは全射にはならない。自乗して負になる実数は存在しないからである。
• 任意の集合 テンプレート:Mvar において、テンプレート:Mvar 上の恒等変換 ${\text{id}}_X:X\ni x\mapsto x\in X$ は全射（実は双射）である。
• デカルト積 テンプレート:Math の各成分への射影 $p_A:A\times B\ni (a,b)\mapsto a\in A,p_B:A\times B\ni (a,b)\mapsto b\in B$は全射である。
• 実2次多項式全体 ${ℝ}_2[x]:=\{a{x}^2+bx+c;(a,b,c)\in (ℝ\setminus \{0\})\times ℝ\times ℝ\}$ から $ℝ$ への写像 テンプレート:Mvar を $D(a{x}^2+bx+c):=b^2-4ac$ と定義すると、テンプレート:Mvar は全射である（任意の $r\in ℝ$ に対して、例えば $x^2-r/4\mapsto r$ である）。
• 正の整数 テンプレート:Mvar に対し、$\det :M_n(ℝ)\ni A\mapsto \det A\in ℝ$は全射である（ここで $M_n(ℝ)$は実 テンプレート:Mvar 次正方行列全体であり， $\det A$は行列式を表す）．実際，任意の実数 テンプレート:Mvar に対して、対角行列 テンプレート:Math の行列式は テンプレート:Mvar である。
• 指数関数$\exp :ℝ\ni x\mapsto e^x\in (0,\mathrm{\infty })$ は全射である．実際，任意の$y\in (0,\mathrm{\infty })$ に対して，$x:=\log y$ ととれば$\exp (x)=e^x=y$である．
• 複素数に対してその実部，虚部，絶対値を与える写像$\mathrm{\Re }:ℂ\ni z\mapsto (z+\bar{z})/2\in ℝ,\mathrm{\Im }:ℂ\ni z\mapsto (z-\bar{z})/2i\in ℝ,|\cdot |:ℂ\ni z\mapsto \sqrt{\mathrm{\Re }(z{)}^2+\mathrm{\Im }(z{)}^2}\in ℝ$はいずれも全射である．

平面上に表した全射の模式図。函数 f: X → Y; y = f(x)（X = 函数の定義域, Y = 函数の値域）。値域の各元の上に定義域の元が規則 f に従って写される（定義域の複数の元が値域の同じ元に写ってもよい）。

左： f が全射になるような定義域の一つ。

右： 二つの定義域 X₁, X₂ が示されているが、何れの場合も f は全射になる。

平面上に表した全射でない場合の模式図。余域 Y の一部の元 y は適当な x ∈ X をとって y = f(x) と書けるが、そうは書けない部分もある。

左： y₀ は Y に属すが、y₀ = f(x₀) となる x₀ ∈ X がない。

右： y₁, y₂, および y₃ は Y の元だが、y₁ = f(x₁), y₂ = f(x₂), および y₃ = f(x₃) となるような x₁, x₂, および x₃ は X の中には無い。

性質

写像が双射（全単射）となるのは、それが単射かつ全射となることと同値である。

函数を（よくやるように）そのグラフと同一視して考えるとき、単射性とは異なり、全射性を函数のグラフのみから読み取ることはできない。全射性は函数自体の性質というよりは函数と余域との関係性と見るべきものである。

右可逆性

写像 テンプレート:Math が写像 テンプレート:Math の右逆写像であるとは、テンプレート:Math（つまり テンプレート:Mvar の効果が テンプレート:Mvar によって打ち消される）が テンプレート:Mvar の各元 テンプレート:Mvar で成り立つときに言う。言葉を変えれば、テンプレート:Mvar と テンプレート:Mvar とのこの順番での合成 テンプレート:Mvar が テンプレート:Mvar の定義域 テンプレート:Mvar 上の恒等写像 テンプレート:Math となるとき、テンプレート:Mvar が テンプレート:Mvar の右逆であるという。逆順の テンプレート:Mvar が テンプレート:Mvar の定義域 テンプレート:Mvar 上の恒等写像でないかもしれないから、写像 テンプレート:Mvar は必ずしも テンプレート:Mvar の（完全）逆写像であるわけではない。即ち、テンプレート:Mvar は テンプレート:Mvar を打ち消すが、逆は必ずしも成り立たない。

右逆を持つ任意の写像は全射であるが、「任意の全射が右逆写像を持つ」という命題は選択公理に同値である。

テンプレート:Math が全射で テンプレート:Mvar が テンプレート:Mvar の部分集合であるとき、テンプレート:Math が成り立つ。つまり テンプレート:Mvar はその原像 テンプレート:Math から回復される。

全型射との関係

右消約性

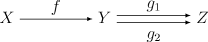
写像 テンプレート:Math が全射となる必要十分条件は、それが右消約的であること、即ち「与えられた写像 テンプレート:Math2 が テンプレート:Math を満たす限り常に テンプレート:Math が言えること」である。この性質は、写像とその合成によって定式化されているから、より一般に圏における射 (morphism) とその合成についての性質に一般化できる。即ち、右消約的な射はエピ射あるいは全型射（圏論的全射）であるという。写像が（集合論的）全射 (surjection) ならば、それはちょうど集合の圏における全型射 (epimorphism) になっている。接頭辞の テンプレート:Lang はギリシャ語で「上の」を意味する言葉である。

右逆型射をもつ任意の射は全型射であるが、逆は一般には正しくない。射 テンプレート:Mvar の右逆 テンプレート:Mvar は テンプレート:Mvar に対するテンプレート:Ill2と呼ばれ、右逆を持つ射は分裂型全型射 (split epimorphism) であるという。

二項関係としての全射

域 テンプレート:Mvar および余域 テンプレート:Mvar を持つ任意の写像は（そのグラフと同一視することにより）、テンプレート:Mvar と テンプレート:Mvar との間の左全域的かつ右一意な二項関係と見ることができる。従って、域 テンプレート:Mvar, 余域 テンプレート:Mvar をもつ全射は、テンプレート:Mvar と テンプレート:Mvar との間の左全域的、右一意かつ右全域的な二項関係ということになる。

全射の始域の濃度

全射の始域の濃度は、余域の濃度以上である。つまり テンプレート:Math が全射ならば、テンプレート:Mvar は少なくとも テンプレート:Mvar の元の（濃度の意味での）個数と等しい数の元を含む。ただし、このことの証明には、テンプレート:Mvar の任意の元 テンプレート:Mvar に対して テンプレート:Math を満たす写像 テンプレート:Math の存在を言うために選択公理が必要になる。テンプレート:Mvar が単射であることを見るのは容易であるから、定義により テンプレート:Math が得られる。

特に、テンプレート:Mvar と テンプレート:Mvar が同じ数の元を持つ有限集合であるときには、テンプレート:Math が全射であることと テンプレート:Mvar が単射であることとが同値になる。

合成と分解

合成が全射（先に施す写像が全射でなくともよいことがわかる）

全射同士の合成は常に全射である。即ち、テンプレート:Mvar および テンプレート:Mvar がともに全射で、テンプレート:Mvar の余域が テンプレート:Mvar の定義域と等しいとき、合成写像 テンプレート:Mvar は全射になる。逆に、合成 テンプレート:Mvar が全射ならば テンプレート:Mvar は全射（だが先に施すほうの テンプレート:Mvar は必ずしも全射でなくてよい）。この性質は、集合の圏における全射から任意の圏における任意の全射に一般化される。

任意の写像は、全射と単射との合成の形に分解することができる。即ち、テンプレート:Math を任意の写像とすれば、全射 テンプレート:Math と単射 テンプレート:Math で テンプレート:Math を満たすものが存在する。これを見るには、集合 テンプレート:Mvar は テンプレート:Mvar の部分集合族 $Y:=\{h^{-1}(z)=\{x\in X\mid h(x)=z\}\mid z\in h(X)\}$ として定めればよい。ここに現れた原像は互いに交わりを持たず、テンプレート:Mvar の分割を与える。このとき、テンプレート:Mvar として各元 テンプレート:Math を テンプレート:Mvar を含む テンプレート:Mvar の元へ写す写像 $f:x\mapsto \{x^{\prime }\in X\mid h(x^{\prime })=h(x)\}$ をとり、テンプレート:Mvar として テンプレート:Mvar の各元が含む テンプレート:Mvar の元が テンプレート:Mvar によって写されるところの テンプレート:Mvar の元へ写す写像 $g:h^{-1}(z)\mapsto z$ とすれば、テンプレート:Mvar は射影ゆえ全射で、テンプレート:Mvar は作り方から単射となり、テンプレート:Math が成り立つ。

誘導された全射・双射

任意の写像はその終域を値域にまで制限することにより全射を誘導し、任意の全射は同じ決まった値に写るような定義域の元を同一視して潰すような商集合の上の全単射を誘導する。きちんと述べれば、任意の全射 テンプレート:Math は以下に述べるように全単射と射影の合成に分解される。テンプレート:Mvar を テンプレート:Math で定められる同値関係による テンプレート:Mvar の同値類全体の成す集合とする。テンプレート:Mvar を f による原像全体の成す集合とするといっても同じことである。写像 テンプレート:Math を テンプレート:Mvar の各元 テンプレート:Mvar をその同値類 テンプレート:Math へ写す射影とし、テンプレート:Math を $f_P([x{]}_{\sim }):=f(x)$ で与えられるよく定義された写像とすればこれは全単射で、テンプレート:Math が成り立つ。

数え上げ

包除原理の応用として、有限集合 テンプレート:Mvar から テンプレート:Mvar への全射の数は

$n!S(m,n)=\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(n-k{)}^m$

により与えられる。ここで テンプレート:Mvar, テンプレート:Mvar は有限集合 テンプレート:Mvar, テンプレート:Mvar の濃度であり、テンプレート:Math は第二種スターリング数である。

参考文献

• テンプレート:Cite book
• テンプレート:Cite book
• テンプレート:Citation
• テンプレート:Cite book

関連項目

• 単射
• 全単射
• 同値関係
• 中への写像

外部リンク

• テンプレート:MathWorld
• テンプレート:PlanetMath