積 (圏論)
圏論において、考えている圏の二つの(あるいはそれ以上の)対象の(圏論的)積(せき、テンプレート:Lang-en-short)または直積 (direct product) は集合の直積(デカルト積)、群の直積、環の直積、位相空間の直積といった数学の他の分野における構成の背後にある本質を捉えるために考えられた概念である。本質的に対象の族の積は与えられた対象のそれぞれへの射をもつ「最も一般な」対象である。
定義
テンプレート:Mvar を適当な対象 テンプレート:Math をもった圏とする。テンプレート:Math と テンプレート:Math との積とは、テンプレート:Math と書かれる テンプレート:Mvar の対象と二つの射 テンプレート:Math および テンプレート:Math との組で、以下の普遍性を満たすものを言う。
- 積の普遍性 (二対象の場合)
- 任意の対象 テンプレート:Mvar および射の対 テンプレート:Math および テンプレート:Math が与えられたとき、一意的な射 テンプレート:Math が存在して、図式

積の普遍性を表す可換図式
一意的な射 テンプレート:Mvar は テンプレート:Math と テンプレート:Math との射の積と言い、テンプレート:Math とも書かれる。射 テンプレート:Math は自然な射影、標準射影 (テンプレート:En) あるいは射影射 (テンプレート:En) と呼ばれる。
いま定義したものは、二項の積であるが、より一般に集合 テンプレート:Mvar で添字付けられた対象の任意の族をとり、それらの積を考えることができる。すなわち、
圏 テンプレート:Mvar の対象の族 テンプレート:Math の(テンプレート:Mvar における)積とは、テンプレート:Mvar の対象 テンプレート:Mvar と射の族 テンプレート:Math との組で以下の普遍性を満足するものを言う。
- 積の普遍性
- 任意の対象 テンプレート:Mvar と射の族 テンプレート:Math が与えられたとき、一意的な射 テンプレート:Math が存在して、次の図式

積の普遍性
この積 テンプレート:Mvar をしばしば テンプレート:Math で表す。テンプレート:Math の場合は特に テンプレート:Math のように書き、射の積も テンプレート:Math のように書く。
等式的な定義
図式を用いる代わりに、対象の積を等式的に定めることができる。その場合例えば、二項の積は
- 一意な射 テンプレート:Mvar が存在することは、二項演算 テンプレート:Math の存在性によって保障される。
- 図式の可換性は等式 テンプレート:Math が任意の テンプレート:Math について成り立つことによって保障される。
- テンプレート:Mvar の一意性は任意の テンプレート:Mvar に対し等式 テンプレート:Math が成り立つことによって保証される[1]。
極限として
積は極限の特別な場合である。これを見るには、極限の定義で必要となる図式において離散圏(恒等射以外の射をもたない対象からなる族)を用いればよい(各離散対象は成分と射影の添字を与え、図式を関手とみれば(離散圏とみた)添字集合 テンプレート:Mvar からの関手である)。このとき実際に積の定義が極限の定義と一致することがみてとれる。テンプレート:Math がテンプレート:仮リンク、射影が極限(極限錐)である。
普遍構成
極限が普遍構成の特別な場合であるのと全く同じように、積もそうである。極限の普遍性を適用するのに必要なものとして、テンプレート:Mvar をただ二つの対象をもつ離散圏とする(このとき テンプレート:Mvar は単にテンプレート:仮リンク テンプレート:Math である)。対角関手 テンプレート:Math は各対象 テンプレート:Mvar に順序対 テンプレート:Math を対応させ、各射 テンプレート:Mvar に順序対 テンプレート:Math を対応させるものである。テンプレート:Mvar における積 テンプレート:Math は、対角函手 テンプレート:Math から テンプレート:Math の対象 テンプレート:Math への普遍射によって与えられる。この普遍射は テンプレート:Mvar の対象 テンプレート:Mvar と射 テンプレート:Math からなり、これは射影を含んでいる。
例
集合の圏における(圏論的な意味での)積はデカルト積(集合の直積)である。与えられた集合の族 テンプレート:Math に対する積は、集合 テンプレート:Math と自然な射影の族 テンプレート:Math との組として定まる。ここで各射影は テンプレート:Math を満たす写像である。 テンプレート:Anchors 任意の集合 テンプレート:Mvar と写像の族 テンプレート:Math が与えられたとき、普遍射 テンプレート:Math は テンプレート:Math として定まる。
他の例:
- 位相空間の圏における積は、各因子の台集合のデカルト積を台として積位相を入れた空間である。積位相はすべての射影が連続であるようなテンプレート:仮リンクである。
- 一つの環 テンプレート:Mvar 上の加群の圏における積は、台集合のデカルト積に成分ごとの加法と分配的な積を入れたものである。
- 群の圏における積は、台集合のデカルト積に成分ごとの積を入れた群の直積によって与えられる。
- 関係の圏 テンプレート:Math において、積は非交和によって与えられる。(集合の圏 テンプレート:Math が テンプレート:Math の部分圏であることを考えるとこれは少し驚かれるかもしれない。)
- 代数多様体の圏において、圏論的な積はテンプレート:仮リンクによって与えられる。
- テンプレート:仮リンク (semi-abelian monoid) の圏において、圏論的な積は history monoid によって与えられる。
- 半順序集合は順序関係を射として用いることで圏として扱うことができる。この場合積と余積は最大下界と最小上界(交わりと結び)に対応する。
議論
任意の圏において、必ずしも積が存在するとは限らない。例えば、空積(すなわち添字集合 テンプレート:Mvar が空集合)は終対象と同じであり、無限群の圏のようないくつかの圏は終対象を持たない: 任意の無限群 テンプレート:Mvar に対し、射 テンプレート:Math は無限個存在するので、テンプレート:Mvar が終対象となることはありえない。
添字集合 テンプレート:Mvar に対し、テンプレート:Mvar で添字付けられる任意の族が圏 テンプレート:Mvar において積を持つならば、積をとる演算を取り纏めて関手 テンプレート:Math として扱うことができるテンプレート:Sfn。この関手が対象をどのように写すかは明らかだが、射の対応は微妙である(定義節で与えられた「射の積」とは少々異なる)。二項の積(積函手はテンプレート:仮リンク)の場合を考えると、必要となるのは テンプレート:Math に対して適当な テンプレート:Math なる射を作ることで、それには積 テンプレート:Math を取ればよい。射に対するこの演算を射の直積あるいはデカルト積 (cartesian product of morphisms) と呼ぶ[2]。一般の場合の積関手も同様に、族 テンプレート:Math の間の射の族 テンプレート:Math に対して テンプレート:Math なる射として、射の族 テンプレート:Math の積 テンプレート:Math が対応する。
対象のすべての有限集合が積をもつような圏はデカルト圏 (cartesian category) と呼ばれることもある[2]。(ただし、「すべての有限極限をもつ圏」の意味でこの語を用いる文献もある。)
積は結合的である。デカルト圏 テンプレート:Mvar において、上で述べたように積函手を考え、テンプレート:Mvar の終対象を テンプレート:Math と書けば、テンプレート:仮リンク
が成立する。これらの性質は(同型を等式で置き換えれば)可換モノイドの性質と形の上では同じである。すなわち、有限積を備えた圏は、テンプレート:仮リンクモノイド圏を構成する。
分配性
有限積および有限余積をもつ圏において、自然な射 テンプレート:Math が存在する、ただしここでプラス記号は余積を表す。これを見るために、次の図式
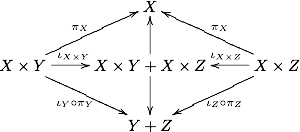
を埋める種々の射影および入射について注意を払わねばならない。
これにより テンプレート:Math に対する普遍性は一意な射 テンプレート:Math を保証する。テンプレート:仮リンクは、この射が実際に同型射となるような圏を言う。従って分配圏において自然な同型
が成立する。
関連項目
参考文献
- テンプレート:Cite book
- テンプレート:Cite book Chapter 5.
- テンプレート:Cite book
- Definition 2.1.1 in テンプレート:Cite book
外部リンク
- Interactive Web page which generates examples of products in the category of finite sets. Written by Jocelyn Paine.
- テンプレート:Nlab