極小曲面

テンプレート:Distinguish 数学または物理学において、極小曲面（きょくしょうきょくめん、テンプレート:Lang-en-short、テンプレート:Lang-fr-short、テンプレート:Lang-de-short、テンプレート:Lang-zh-short）とは局所的にその面積を最小化する曲面である。

これはテンプレート:日本語版にない記事リンクが零をもつことと同じである（以下の定義を見よ）。

解説

「極小曲面」の用語はこれら曲面が本来ある一定の面積を合計として最小にする曲面としてであるから用いられる。極小曲面の面積を最小化する物理的モデルは、テンプレート:日本語版にない記事リンクが生じる、石鹸液に針金の枠を漬けることで作ることができる。それはその針金枠を境界とする極小曲面である。しかしながら、その用語は自己交差や制約されないより一般的な曲面についても用いられる。そこで与えられた制約条件は面積の異なる幾つかの極小曲面をも成り立たせる（例えば、テンプレート:日本語版にない記事リンクを見よ）：標準的な定義は局所的最適に関係するだけで、大域的最適ではない。

直観的には、或る極小曲面は、最小を充たす摂動の適用における変数のところのその面積または体積が与えられる曲面である。その極小曲面はつまり（十分小さくかつ十分限定された或る摂動の結果からみて長さが増加するしかないところの）測地線より高い次元において相似物として形成される。

定義

極小曲面は $ℝ^{3}$ において、幾つかの同値な方法により定義できる。それらが同値である事実は極小曲面の理論がいかに幾つもの数学上の分野にまたがっているかを示す、とりわけ微分幾何学、変分法、ポテンシャル論、複素解析そして数理物理学^[1]。

局所最小面積定義（テンプレート:Lang-en-short）：おなじ境界をもつすべての曲面のうち最小の面積をもつ、単純閉曲線により境界づけられた、曲面

M \subset ℝ^{3}

は、任意の点 p ∈ Mが近傍をもてば、そのときに限り極小である。

この性質は局所的である：より小さな面積のおなじ境界をもつその他の曲面とともに、極小曲面では領域が存在しなければならない。この性質は石鹸膜に関連して確立された；境界としての針金枠に、極小の面積になるよう石鹸膜は形作られる。

変分的定義（テンプレート:Lang-en-short）：曲面

M \subset ℝ^{3}

は、コンパクトに支持されたすべての変分に対する面積関数の臨界点であれば、そのときに限り極小である。

この定義は、長さ関数の臨界点として類似に定義されるものである、測地線に対する2次元の類似として極小曲面を成り立たせる。

平均曲率的定義（テンプレート:Lang-en-short）：曲面

M \subset ℝ^{3}

は、すべての点でそのテンプレート:日本語版にない記事リンクが零に等しければそのときに限り極小である。

この定義の直接な意味は、曲面上の任意の点は等しくかつ相対する主曲率の鞍点であるということである。さらに言えば、これは、極小曲面がテンプレート:日本語版にない記事リンクの静的な解を与えることを示す。ヤング・ラプラスの式により、石鹸膜の平均曲率はその側面の圧力差に比例する。もしある領域で石鹸膜が囲まれていなければ、そのときこれはその平均曲率が零になることを成り立たせる。

微分方程式による定義（テンプレート:Lang-en-short）:曲面

M \subset ℝ^{3}

はもしそれが次式の解のグラフとして局所的に表されるならばそのときに限り極小である：

(1 + u_{x}^{2}) u_{y y} - 2 u_{x} u_{y} u_{x y} + (1 + u_{y}^{2}) u_{x x} = 0

この定義のその偏微分方程式はもともと1762年にラグランジュにより見つけられた^[2]、そしてジャン＝バティスト・ムーニエは1776年に平均曲率が消えることを意味していることを見出した^[3]。

エネルギーによる定義（テンプレート:Lang-en-short）：ある等角なはめ込み

X : M \to ℝ^{3}

は、もしすべての支持するコンパクトな多様体についてのディリクレエネルギーの臨界点であるならばそのときに限り極小である。または同値として、もし任意の点

p \in M

が、その境界に比例した最小のエネルギーをもつ近傍をもてば極小である。

この定義は極小曲面を調和関数とポテンシャル論とに結び付ける。

調和的定義（テンプレート:Lang-en-short）：もし

X = (x_{1}, x_{2}, x_{3}) : M \to ℝ^{3}

が、あるリーマン面の3次元空間への等長的はめこみならば、

x_{i}

が各

i

の

M

における調和関数であるときはいつでも、

X

は極小であるという。

この定義と調和関数の最大値原理の直接的な意味は、 $ℝ^{3}$ にはコンパクトで完備な極小曲面は無いことである。

ガウス写像による定義（テンプレート:Lang-en-short）：ある曲面

M \subset ℝ^{3}

は、ステレオな投影であるガウス写像

g : M \to

ℂ \cup {\infty}

が、もととなるリーマン面の構造に関して有理型であり、かつ'球面の一部'（テンプレート:Lang-en-short）ではないときに限り極小である。

この定義は、そのガウス写像のその導関数と関係する、平均曲率がテンプレート:仮リンクの跡の半分であることを用いる。もし投影されたガウス写像がコーシー・リーマン方程式に従うならば、この場合それは球面の一部であって、跡は消えるかまたは $M$ の各点はテンプレート:日本語版にない記事リンクである。

局所最小面積定義と変分的定義は $ℝ^{3}$ よりも高次のリーマン多様体へ拡張して定義することを極小曲面に与える^[4]。

歴史

極小曲面の理論はラグランジュが1762年に、与えられた閉じた輪郭に交差して引き伸ばされる最小の面積の曲面 $z = z (x, y)$ を探す変分問題を考えたときに始まる。彼はその解に対して次のオイラー＝ラグランジュ方程式を導いた：

\frac{d}{d x} (\frac{z_{x}}{\sqrt{1 + z_{x}^{2} + z_{y}^{2}}}) + \frac{d}{d y} (\frac{z_{y}}{\sqrt{1 + z_{x}^{2} + z_{y}^{2}}}) = 0

彼は平面以外に何らの解も見つけることにはならなかった。1776年にジャン＝バティスト・ムーニエはテンプレート:日本語版にない記事リンクとテンプレート:日本語版にない記事リンクがその方程式を満たすこと、および微分の表現がその曲面のテンプレート:日本語版にない記事リンクの二倍に関係すること、結論として零平均曲率をもつ曲面は面積極小であることを見出した。

ラグランジュの方程式を次のように拡張することによって：

(1 + z_{x}^{2}) z_{y y} - 2 z_{x} z_{y} z_{x y} + (1 + z_{y}^{2}) z_{x x} = 0

ガスパール・モンジュとアドリアン＝マリ・ルジャンドルは1795年に解の曲面についての式の表現を導いた。テンプレート:日本語版にない記事リンクが1830年にテンプレート:仮リンクを導いたことによってこれらが成功したときに、彼らは実際には役立たないものとして一般的に見なした。ウジェーヌ・シャルル・カタランは1842年と1843年に螺旋面が唯一のテンプレート:日本語版にない記事リンクの極小曲面であることを証明した。

'複素解析の方法'（テンプレート:Lang-en-short）によりテンプレート:日本語版にない記事リンクが解かれた、その世紀の半ばまで明らかに進歩は低下した。しかし極小曲面の「最初の黄金時代」は始まった。シュワルツは複素解析の方法によりテンプレート:日本語版にない記事リンクの正四角形についての解を1865年に、そして一般の四角形について（彼の周期的テンプレート:日本語版にない記事リンクの構成により）1867年に見出した。ワイエルシュトラスとテンプレート:日本語版にない記事リンクは、極小曲面を複素解析と調和関数とに強固に結びつける、もっと便利なテンプレート:日本語版にない記事リンクを開発した。他の重要な寄与はテンプレート:仮リンク、ダルブー、ベルトラン、ボンネ、リー、リーマン、テンプレート:仮リンクからあった。

1925年から1950年にかけて、極小曲面の理論は復活した、今では主に'非媒介変数表示極小曲面'（テンプレート:Lang-en-short）が指向されている。ジェス・ダグラスとテンプレート:日本語版にない記事リンクによるプラトーの問題の完全な解決は主な金字塔である。^[6]テンプレート:日本語版にない記事リンクと'有限総曲率'（テンプレート:Lang-en-short）の'完備極小曲面'（テンプレート:Lang-en-short）に関するテンプレート:日本語版にない記事リンクの業績も重要である。

またの復活が1980年代に始まった。一つの契機は1982年のセルソ・コスタによるテンプレート:仮リンクの発見である。これは、平面、懸垂面、螺旋面だけが有限な位相的な型の $ℝ^{3}$ で完全に埋め込まれた極小曲面であることの予想を証明するものである。これは古い媒介変数的方法を用いた新しい成果を刺激するのみならず、研究された曲面を可視化するコンピューターグラフィックスと（大きな対称な曲面へ組み入れることができる、曲面の'切れ端'（テンプレート:Lang-en-short）を決める、テンプレート:仮リンクを用いるときに、一定の媒介変数ははめ込まれる曲面をつくるよう数値的に適合することが必要になる）「区間問題（テンプレート:Lang-en-short）」を解く数値的方法の重要性を示した。別の契機はH.カルチャー（テンプレート:Lang-en-short）による証明である。これはもともと1970年にアラン・ショーンによって経験的に述べられたテンプレート:日本語版にない記事リンクが実在することである。これは有意義な曲面の族と、古い曲面から例えばそれらに把手（とって、テンプレート:Lang-en-short）を付けたり捻じ曲げたりすることで、新しい曲面を派生する方法を導き出した。

現状では、極小曲面の理論は取巻く他の幾何学における極小部分多様体の理論に多様化して、数理物理学（例えば、テンプレート:仮リンク、テンプレート:日本語版にない記事リンク）と三次元多様体の幾何学（例えば、テンプレート:日本語版にない記事リンク、ポアンカレ予想、幾何化予想）に関係するようになった。

例

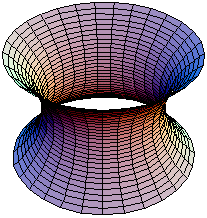
極小曲面の古典的な具体例は以下を含む：

自明な場合として、平面
テンプレート:日本語版にない記事リンク：懸垂線をその回転軸に1周して作られる極小曲面
テンプレート:日本語版にない記事リンク：その直線に垂直なひとつの回転軸のまわりに一定の速度で回転しながら、一定の速度をもって回転軸に沿って同時に進む直線によって描かれる曲面

懸垂面と螺旋面は、一方から他方への連続変形があることを与えられるという特筆に価する性質を有する。その局所的な変形はすべての点において等長である。加えて、変形途中のすべての曲面は極小曲面である。^[7]これらについて、懸垂面を表す変数値0から螺旋面を表す変数値 $\frac{π}{2}$ までの、 $t$ を変形の媒介変数として、そして次に示す $t$ からの変形途中の曲面を表す変数の $(u, v)$ である、媒介変数表示を私たちは容易に得る：

x = \frac{e^{u} \cos (v - t)}{2} + \frac{e^{- u} \cos (v + t)}{2}

y = \frac{e^{u} \sin (v - t)}{2} + \frac{e^{- u} \sin (v + t)}{2}

z = u \cos (t) + v \sin (t)

テンプレート:Clear

19世紀の黄金時代からの曲面は以下を含む：

テンプレート:日本語版にない記事リンク：

$ℝ^{3}$ を埋めるテンプレート:日本語版にない記事リンク

テンプレート:日本語版にない記事リンク：没後説明された周期的曲面
エネパー曲面
テンプレート:日本語版にない記事リンク：最初に見出された向き付け不可能な極小曲面
テンプレート:日本語版にない記事リンク：自己交差する極小曲面
テンプレート:日本語版にない記事リンク：三重周期極小曲面

現代の曲面は以下を含む：

ジャイロイド：液晶構造にとくに関係する三重曲面の、1970年以来のシェーンの曲面のひとつ。
テンプレート:日本語版にない記事リンクの族：テンプレート:日本語版にない記事リンクの一般化
テンプレート:日本語版にない記事リンク：著名な未証明の定理。テンプレート:日本語版にない記事リンクと後に視覚化したテンプレート:日本語版にない記事リンクによる。ジェームズ・ホフマン、ダビド・ホフマンおよびウィリアム・ミークス3世はそのとき異なった回転対称をもつ曲面の族を導く定義を拡張した。
エンネパー曲面に把手を付けた、テンプレート:日本語版にない記事リンクの族テンプレート:Clear

零でない一定のある曲率をもつ、球面は、用語の規定の意味において極小曲面ではない。それは別の極小の意味においてであることを確かめられる：それは一定の体積を内包して面積が極小である曲面である（等周定理の項を見よ）。

数学的性質

偏微分方程式

$ℝ^{3}$ に横たわる或る曲面は、二変数 $u$ と $v$ からなる或る関数のグラフの如き表現である（ユークリッド）座標の変換により、局所化を与えられる。詳しくは、その曲面は座標の点の組み合わせに分解される：

\vec{M} = (\begin{matrix} u \\ v \\ f (u, v) \end{matrix})

,

記法 $\frac{\partial f}{\partial u} = f_{u}$ と $\frac{\partial^{2} f}{\partial u^{2}} = f_{u u}$ を用いて、オイラー-ラグランジュによる局所的方程式に書き直される：

f_{u u} (1 + f_{v}^{2}) - 2 f_{u} f_{v} f_{u v} + f_{v v} (1 + f_{u}^{2}) = 0 .

この方程式は一次と二次の階数の $f$ のその偏微分を導く証拠とよばれる或る関係を示す：これは偏微分方程式の一例である。

例：式 $z = f (v / u)$ の解による唯一の族はテンプレート:日本語版にない記事リンクである。式 $z = f (u) + g (v)$ の解による唯一の族はテンプレート:日本語版にない記事リンクである。

同様にもしそれらが反‐直観的に思われるのを与えるならば、それはプラトーの問題の解の唯一性が存在しない。言い換えれば、それは単独の極小曲面が与えれられた条件では定まらないことを示す。すなわち'輪郭'（テンプレート:Lang-fr-short）に対する極小曲面の個数に関して如何なるものかである：
- もし輪郭が或る平面曲線であるならば、それは或る極小曲面を囲む。同様にしてもしそれが或る平面への単なる射影であるならば或る凸状曲線に沿う（Rado,1932）。
- 曲率の合計が $4 π$ 以下である曲線は円盤状の極小曲面の'境界'（テンプレート:Lang-fr-short）を与える。
- 解析的曲線（テンプレート:Lang-fr-short）は、有限の個数の、面積が極小である曲面の境界を与える。

モース理論の応用

モース理論は、臨界点の計算についての有効性を十分に上げる；有限次元のコンパクト空間において定義された或る関数の臨界点の個数を評価するのを含めて成し遂げるところの、モース不等式をもつことでそれは有名である。曲率が零の曲面は面積あるいは体積の臨界点として呈する。それはモース理論の応用を試みられる：とかくするうちに、曲面における'変分'（テンプレート:Lang-fr-short）は無限次元での検討の必要性を導く。コンパクト性は基本的な位相の性質において依存していることを与えない^[8]。

それでも、類似の理論が成り立ち恒等式を与える：

(- 1)^{Y_{1}} + (- 1)^{Y_{2}} + . . . + (- 1)^{Y_{n}} = 1,

ここで $n$ は異なる極小曲面の個数であり、すべての $Y_{n}$ は、極小曲面毎に関係する特性数である。

一般化と他分野との関係

極小曲面は $ℝ^{3}$ 以上の、テンプレート:日本語版にない記事リンク、高次元空間、またはリーマン多様体のような、他の多様体でも定義できる。

極小曲面の定義はテンプレート:日本語版にない記事リンクに一般化または拡張できる：必ずしも零である必要はない、平均曲率を有する曲面。

等温曲面（テンプレート:Lang-en-short）の曲率線（テンプレート:Lang-en-short）は等温網（テンプレート:Lang-en-short）を成す^[9]。

テンプレート:日本語版にない記事リンクでは離散極小曲面が研究される：頂点の位置の'微動'（テンプレート:Lang-en-short）のもとで面積を最小化する三角形による複体^[10]。そのような離散化はしばしば、閉じた表現が知られていない表示においても、数値的に極小曲面を近似するのに用いられる。

極小曲面上のブラウン運動は、極小曲面に関する幾つかの定理の、確率論的な証明を導出する^[11]。

合成物の素材の自己集合での予想された応用により、特にテンプレート:日本語版にない記事リンクと材料工学の分野で、極小曲面は甚だしい科学の研究の一分野になった^[12]。細胞生物学で重要な構造の、小胞体は、非自明な極小曲面に従う進化の圧力のもとにおかれるよう提案された^[13]。

一般相対性理論とローレンツ幾何学では、テンプレート:日本語版にない記事リンクとして知られる、極小曲面の概念の確かな拡張と修正はは顕著である^[14]。事象の地平線と対照的に、それらはブラックホールの境界の理解への曲率に基づいた接近法を示す。

テントのように、極小曲面による構造は用いられる。

極小曲面は現代のデザイナーによって用いられるテンプレート:日本語版にない記事リンクの道具箱の一部である。建築においては、極小曲面に大いに関係する張力構造において多大な興味をもたれてきた。フライ・オットー、坂茂、ザハ・ハディッドの仕事において著名な事例がみられる。フライ・オットーによるミュンヘン・オリンピック競技場の計画は石鹸膜に着想を得ている^[15]さらにフライ・オットーによる別の著名な事例は、カナダのモントリオールのテンプレート:仮リンクでのドイツ館である^[16]。

美術界ではとりわけ、テンプレート:日本語版にない記事リンク（ 1927 - 2018 ）、テンプレート:日本語版にない記事リンク（ 1949 - ）、およびテンプレート:日本語版にない記事リンク（ 1929 - 2011 ）の彫塑において、極小曲面は発展的に開花してきた。

毛細管現象

テンプレート:Main

或る場合、石鹸の膜によって私たちは或る極小曲面を造ることを得る。この場合、石鹸膜は、この曲面が働くことを促すものである、ポテンシャルエネルギーに従い極小になってゆく。より詳しくは、それはラプラス‐ヤング方程式に従う： $Δ p = 2 σ γ$ ；ここに $Δ p$ はその曲面の二つの断面で与えられる圧力差を示す、 $σ$ はこの曲面を形成させるものである液体により特徴づけられる、表面張力、そして $γ$ は平均曲率である。石鹸膜が生じている場合において、その空気圧は両側から均等にかかる、よって $Δ p = 0$ 、したがって曲率は零である：私たちは極小曲面を数学的に再定義した。

この表現はしかしながら利益が限定される。なにしろ、ポテンシャルエネルギーの安定な釣合いにおけるところの表現ではない。ポテトチップスの形の輪郭を想像してみよ。三つの曲面がこの輪郭に適合することを与えられる、石鹸膜に対応して二つがある、三つ目は不安定である、「幻影」の石鹸膜、これはエネパー曲面からの例に対応する場合である。テンプレート:Clear

脚注または引用文献

テンプレート:Reflist

ウェブサイト

書籍

雑誌

参考文献

テンプレート:参照方法テンプレート:Commons&cat

教科書

R. Courant. Dirichlet's Principle, Conformal Mapping, and Minimal Surfaces. Appendix by M. Schiffer. Interscience Publishers, Inc., New York, N.Y., 1950. xiii+330 pp.
H. Blaine Lawson, Jr. Lectures on minimal submanifolds. Vol. I. Second edition. Mathematics Lecture Series, 9. Publish or Perish, Inc., Wilmington, Del., 1980. iv+178 pp. テンプレート:ISBN
Robert Osserman. A survey of minimal surfaces. Second edition. Dover Publications, Inc., New York, 1986. vi+207 pp. テンプレート:ISBN, テンプレート:Mr
Johannes C.C. Nitsche. Lectures on minimal surfaces. Vol. 1. Introduction, fundamentals, geometry and basic boundary value problems. Translated from the German by Jerry M. Feinberg. With a German foreword. Cambridge University Press, Cambridge, 1989. xxvi+563 pp. テンプレート:ISBN
テンプレート:Cite book
- テンプレート:Cite book 1998年
Ulrich Dierkes, Stefan Hildebrandt, and Friedrich Sauvigny. Minimal surfaces. Revised and enlarged second edition. With assistance and contributions by A. Küster and R. Jakob. Grundlehren der Mathematischen Wissenschaften, 339. Springer, Heidelberg, 2010. xvi+688 pp. テンプレート:ISBN, テンプレート:Doi テンプレート:Closed access, テンプレート:Mr
Tobias Holck Colding and William P. Minicozzi, II. A course in minimal surfaces. Graduate Studies in Mathematics, 121. American Mathematical Society, Providence, RI, 2011. xii+313 pp. テンプレート:ISBN

オンライン文献

テンプレート:Cite web (graphical introduction to minimal surfaces and soap films.)
テンプレート:Cite web (A collection of minimal surfaces with classical and modern examples)
テンプレート:Cite web (A collection of minimal surfaces)
テンプレート:Cite web (Online journal with several published models of minimal surfaces)

外部リンク

テンプレート:Differential-geometry-stub テンプレート:Normdaten

↑ テンプレート:Harvnb
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb
↑ 変分的定義についてはテンプレート:Harvを見よ。
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb、一次文献はテンプレート:Harvnb、テンプレート:Harvnb。
↑ テンプレート:Harvnb
↑ 選ばれた定義がどうであろうと、無限次元多様体は、局所的にコンパクトではない：崩れた、それは大域性の存在を与えない。
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb
↑ テンプレート:Harvnb

[1] テンプレート:Harvnb

[Lagrange1760-2] テンプレート:Harvnb

[Meusnier1785-3] テンプレート:Harvnb

[4] 変分的定義についてはテンプレート:Harvを見よ。

[us_741-5] テンプレート:Harvnb

[6] テンプレート:Harvnb、一次文献はテンプレート:Harvnb、テンプレート:Harvnb。

[7] テンプレート:Harvnb

[8] 選ばれた定義がどうであろうと、無限次元多様体は、局所的にコンパクトではない：崩れた、それは大域性の存在を与えない。

[9] テンプレート:Harvnb

[10] テンプレート:Harvnb

[11] テンプレート:Harvnb

[12] テンプレート:Harvnb

[13] テンプレート:Harvnb

[14] テンプレート:Harvnb

[15] テンプレート:Harvnb

[16] テンプレート:Harvnb

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

極小曲面

目次

解説

定義

歴史

例