黄金比

テンプレート:参照方法 黄金比（おうごんひ、テンプレート:Lang-en-short）とは、次の値で表される比のことである：

$1:\frac{1+\sqrt{5}}{2}.$

黄金長方形（縦横の長さの比が黄金比（ 1: 1.618…）である長方形）から最大正方形を切り落とすと、元の長方形と相似になる。赤線は黄金螺旋、緑線は正方形内の四分円を接続したものである。黄色は重なっている部分を表す。

以下で述べるような数理的な性質は、有理数にならないこの値のみが持つ性質であり、有理近似等には基本的には意味が無い。「デザインを美しくする」などといった巷間よく見られる説については#用途を参照。小数に展開すると 1 : テンプレート:Val あるいは テンプレート:Val : 1 といった値となる。

黄金比は貴金属比の一つである（第1貴金属比）。

幾何的には、テンプレート:Math が黄金比ならば、

テンプレート:Math2

という等式が成り立つことから、縦横比が黄金比の矩形から最大正方形を切り落とした残りの矩形は、やはり黄金比の矩形となり、もとの矩形の相似になるという性質がある。正五角形の1辺と対角線との比は黄金比に等しい。数列 テンプレート:Math2 は、等比数列をなす。そのため、（中項 テンプレート:Mvar と末項 テンプレート:Math2 の比という意味で）中末比（ちゅうまつひ）とも呼ばれる。

線分を2つに分け、短い部分と長い部分の長さの比が、長い部分と全体の長さの比に等しくなるようにしたときの比であるため、外中比（がいちゅうひ、テンプレート:Lang-en-short）とも呼ばれる。黄金比で長さなどを分けることを黄金比分割または黄金分割（テンプレート:Lang-en-short または テンプレート:Lang-en-short）という。

• 
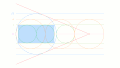
  黄金長方形では、(長辺 - 短辺) : 短辺 = 短辺 : 長辺 が成り立つことを表した図。
• 
  黄金長方形から最大正方形を切り取っていった図（残った長方形も黄金長方形になる）。

黄金比における

$\frac{1+\sqrt{5}}{2}$

を黄金数（おうごんすう、テンプレート:Lang-en-short）という。しばしばギリシア文字の テンプレート:Mvar（ファイ）で表されるが、テンプレート:Mvar（タウ）を用いる場合もある。黄金数は、二次方程式 テンプレート:Math の正の解である：

$\phi =\frac{1+\sqrt{5}}{2}=1.6180339887\cdots$

黄金数の性質

既約多項式

• ${\phi }^2=\phi +1$
  • すなわち、黄金数 テンプレート:Mvar の有理数体 $\mathbb{Q}$ 上の既約多項式は テンプレート:Math である。
  • テンプレート:Mvar は無理数であり、

$\phi =\frac{1+\sqrt{5}}{2}=1.6180339887\cdots$

• ${\phi }^{-1}=\phi -1=\frac{-1+\sqrt{5}}{2}=0.6180339887\cdots$

• 
  黄金数 テンプレート:Mvar について、テンプレート:Math2 を、面積で表した図。青線が、縦横の長さ テンプレート:Math2 の黄金長方形2個を表し、右上にある赤色の網目部分が テンプレート:Math2、左下にある赤色の網目部分が テンプレート:Math を表す。
• 
  黄金数 テンプレート:Mvar について、テンプレート:Math2 を、面積で表した図。縦横の長さが テンプレート:Math2 の黄金長方形（青線）において、斜線部分が等積となる。また、赤色の網目部分は テンプレート:Math2 を表している。

連分数表示

• 黄金数は次の連分数表示を持つ：

$\phi =1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{\ddots }}}}=[1;1,1,1,\cdots ]$

• 次の表示もある：

${\phi }^{-1}=0+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{\ddots }}}}=[0;1,1,1,\cdots ]$

無限多重根号による表示

• 黄金数は次の無限多重根号による表示を持つ：

$\phi =\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{\cdots }}}}}$

• 次の表示もある：

$\phi =\sqrt{2+\sqrt{2-\sqrt{2+\sqrt{2-\sqrt{\cdots }}}}}$

${\phi }^{-1}=\sqrt{2-\sqrt{2+\sqrt{2-\sqrt{2+\sqrt{\cdots }}}}}$

級数表示

• $\phi =\frac{13}{8}+\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}(2n+1)!}{(n+2)!n!4^{2n+3}}$

三角関数による表示

三角関数を使うと次のように表すことができる：

• $\phi =2\cos \frac{\pi }{5}=2\cos 36^{\circ }=-2\cos 6\times 6\times 6^{\circ }$
• $\phi =2\sin \frac{3\pi }{10}=2\sin 54^{\circ }=-2\sin 666^{\circ }$
• $\phi =1+2\sin \frac{\pi }{10}=1+2\sin 18^{\circ }$
• $\phi =1+2\cos \frac{2\pi }{5}=1+2\cos 72^{\circ }$
• $\phi =\frac{1}{2}\csc \frac{\pi }{10}=\frac{1}{2}\csc 18^{\circ }$
• $\phi =\frac{1}{2}\sec \frac{2\pi }{5}=\frac{1}{2}\sec 72^{\circ }$
• ${\phi }^{-1}=2\sin \frac{\pi }{10}=2\sin 18^{\circ }$
• ${\phi }^{-1}=2\cos \frac{2\pi }{5}=2\cos 72^{\circ }$

指数関数による表示

指数関数を使うと次のように表すことができる。

• $\phi =e^{i\frac{\pi }{5}}+e^{i\frac{-\pi }{5}}$

黄金比に関する極限

• $\sum _{n=1}^{\mathrm{\infty }}\frac{n}{{\phi }^{2n}}=1$
• $\sum _{n=1}^{\mathrm{\infty }}\frac{1}{{\phi }^n}=\phi$

フィボナッチ数列との関連

• フィボナッチ数列の一般項テンプレート:Mvarは、黄金数を用いて次のように表される。

$F_n=\frac{1}{\sqrt{5}}\{{\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n\}=\frac{{\phi }^n-(1-\phi {)}^n}{\sqrt{5}}=\frac{{\phi }^n-(-\phi {)}^{-n}}{\sqrt{5}}$

この式は、ビネの公式と呼ばれることがある。

• フィボナッチ数列の隣接2項の比は黄金数に収束する。

$\underset{n\to \mathrm{\infty }}{\lim }\frac{F_{n+1}}{F_n}=\phi$

等比数列 テンプレート:Math2 は、第3項以降がそれぞれ直前の2項の和に等しい性質を幾何学的に表した図。青色、緑色、黄色、赤色の線分は階差を表し、同色どうしは長さが等しくなる。

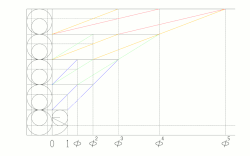
• 等比数列 テンプレート:Math2 において、テンプレート:Math2 より

テンプレート:Math2（テンプレート:Mvar は自然数）

が成り立つ。

テンプレート:Math2,

テンプレート:Math2,

テンプレート:Math2,

テンプレート:Math2,

テンプレート:Math2,

…

となり、係数にフィボナッチ数が出現する。そのため、テンプレート:Mvar は次のように表すことができる。

テンプレート:Math2

さらに、フィボナッチ数と、フィボナッチ数列の同伴リュカ数列であるリュカ数テンプレート:Mvarを用いて、次のように表すこともできる。

テンプレート:Math2

ピゾ数

黄金数はピゾ数であり、ピゾ数の集合の最小の集積点である。そのため黄金数の累乗は、ほとんど整数になる。例えば、

${\phi }^{17}=3571.000280\dots$

${\phi }^{18}=5777.999826\dots$

${\phi }^{19}=9349.000106\dots$

である。黄金数の累乗がほとんど整数になる理由は、該当記事を参照されたい。

幾何学的性質

半径の比が

$(\phi -\sqrt{\phi }):1:(\phi +\sqrt{\phi })$

である3つの円が互いに外接する時、その3つの円の全てと外接する大小2つの円を描くことができ、それらを合わせた5つの円の半径の比は

$(\phi -\sqrt{\phi }{)}^2:(\phi -\sqrt{\phi }):1:(\phi +\sqrt{\phi }):(\phi +\sqrt{\phi }{)}^2$

である。

ここで

$\phi -\sqrt{\phi }=\frac{1}{\phi +\sqrt{\phi }}$

であり、隣接する円との半径の比が同じで、互いに密に接する円の列を螺旋状に無限に配置することができる。

（→デカルトの円定理）

• 
  半径の比が黄金比である2円が外接しているとき、共通外接線2本の交点と、2円の接点の距離は、大きい方の円の直径に等しい。
• 
  半径 テンプレート:Math の円（青線）と半径1の円（緑線）が外接するとき、共通外接線2本の交点と半径1の円周上の点の距離で最短のものは、黄金数に等しい。
• 
  合同な直角二等辺三角形を張り合わせて黄金長方形、白銀長方形（大和比）を作り、それらから正三角形を作った例。
• 
  互いに合同な正方形を活用して黄金比の線分を作り出せることを示した図。図中では同じ長さの辺を持つ正三角形、正方形、正五角形も示されている。
• 
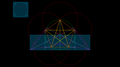
  「半径 2 の正円」（緑色）と「辺の長さが 1 と φ の黄金長方形」（橙色）を活用すると図のように当該正円の円周を20等分する点を求めることができる。

応用

1のn乗根

• 五次方程式 テンプレート:Math を解く過程で黄金数が出現する。

テンプレート:Math2

テンプレート:Math2

そのため、1の1以外の5乗根は次のように表される。

$x=\frac{-\phi \pm i\sqrt{3-\phi }}{2},\frac{\phi -1\pm i\sqrt{\phi +2}}{2}$

• 同様に、1の テンプレート:Math 以外の10乗根は、上記の4つに加えて次のように表される。

$x=\frac{\phi \pm i\sqrt{3-\phi }}{2},\frac{-\phi +1\pm i\sqrt{\phi +2}}{2}$

• 同様に、1の テンプレート:Math 以外の20乗根は、上記の8つに加えて次のように表される。(複合任意)

$x=\frac{\pm \sqrt{3-\phi }\pm i\phi }{2},\frac{\pm \sqrt{\phi +2}\pm i(\phi -1)}{2}$

ゲーム

• ワイソフのゲーム（2山の片方からまたは、両方から同数ずつ取る石取りゲーム）の後手必勝形は

  $(\lfloor n\phi \rfloor ,\lfloor n{\phi }^2\rfloor )$（テンプレート:Mvar は 0 以上の整数、⌊ ⌋ は床関数）

作図

最も簡単な作図方法は下記の通り。

1. 正方形 abcd を描く。
2. 辺 bc の中点 o を取る。
3. 中心を o とし、d (a) を通る円を描き、辺 bc の延長との交点を e とする。
4. 長方形 abef を描く。
5. ab : be は黄金比となる（長方形 abef は黄金長方形）。

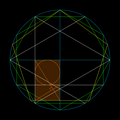
正五角形や五芒星（星形：☆）（何れも作図可能）から容易に作図することができる。正五角形の一辺と対角線の比、五芒星の辺と隣接2頂点の距離の比は、黄金比に等しい。

• 
  互いに合同な直角二等辺三角形を図のように並べると黄金長方形が出来る。
• 
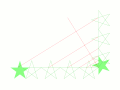
  五芒星に現れる線分の組み合わせから様々な規模での黄金比が生じることを平行線で表した図。
• 
  正円とその中心を通る水平ならびに傾き2の直線との交点を活用すると図のように黄金長方形（赤色・青色・緑色）を描ける。
• 
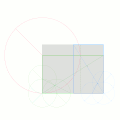
  幾何学的に或る長方形（灰色）からその長辺または短辺の全長を使い切った黄金長方形を切り取る方法の一例。青枠または緑枠で示される長方形が黄金長方形となっている。
• 
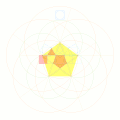
  同一の正円（青色）に内接する正五角形（黄色）と正六角形（緑色）を活用して黄金長方形（橙色）を作り出す例。
• 
  正円（緑色）の半径と同じ長さの辺を持つ正方形（青色）を活用した正五角形（橙色）や五芒星（黄いろ）の描き方の例。赤色の円は描き上げ後の検証のためのもの。
• 
  正円半径と同じ長さの辺の正方形を活用した内接正五角形（五芒星）の描き方の一例。赤色の円は描き上げ後の検証のためのもの。

歴史

ジャック＝ルイ・ダヴィッドの『レカミエ夫人の肖像』（1800年）。構図が安定して見えるのは、夫人の横たわる姿が黄金比の長方形に収まるように構成されているからだという。

伝承では、古代ギリシアの彫刻家ペイディアス（テンプレート:Lang, 紀元前490年頃 - 紀元前430年頃）が初めて使ったといわれる。黄金数の記号φは彼の頭文字であるが、使われ始めたのは20世紀である。なお、τはギリシア語の「分割」に由来し、やはり20世紀に使われ始めた。

同じく古代ギリシアの数学者ユークリッド（紀元前3世紀? - ）の著書『ユークリッド原論』では第6巻の定義3で外中比の定義が記されている。『原論』第6巻の命題30で「与えられた線分を外中比に分ける作図法」が記されている。東京工芸大学教授の牟田淳によると、ローマ建築の理論にも、黄金比の考え方が見られる。

ルネサンス期イタリアの学者レオナルド・ダ・ヴィンチ（1452年4月15日 - 1519年5月2日（ユリウス暦））も発見していた記録が残っている。彼が描いた有名な美人画『モナ・リザ』の顔は黄金比になっているという指摘もある。

ダ・ヴィンチの同時代人であったルカ・パチョーリは著書で『神聖比例論』として言及した。「黄金比」という用語が文献上に初めて登場したのは1835年刊行の、ドイツの数学者マルティン・オーム（「オームの法則」で有名なゲオルク・オームの弟）の著書『初等純粋数学』。また、1826年刊行の初版にはこの記載がないことから、1830年頃に誕生したと考えられる。

用途

長方形は縦と横の長さの比が黄金比になるとき、安定した美感を与えるという説がある。これはグスタフ・フェヒナーの1867年の実験を論拠としている。しかし、フェヒナーの実験の解釈については否定的な様々な見解がある。1997年に国際経験美学会誌の黄金分割特集では、この実験結果を「永遠に葬るもの」とする見解が掲載された。また類似の（すなわち、同様に根拠が極めてあやしい）安定した比とされるものに白銀比があるテンプレート:Efn。

黄金比は、長方形の形状の物の縦横比に利用されることが多い。例えば、名刺やクレジットカードをはじめとする様々なカード類などは、短辺と長辺の比率が1対1.6台であることが多い。

ディスプレイのアスペクト比には、WQXGA（解像度2560x1600）、WUXGA（同1920x1200）など、黄金比に近い8:5 (16:10) のものもある。

黄金比はパルテノン神殿やピラミッドといった歴史的建造物や美術品の中に見出すとされてきたが、これらは後付けの都市伝説であるものが含まれる。一方で、意図的に黄金比を意識して創作した芸術家も数多い。

自然界に存在する植物の葉脈や巻貝の断面図など対数螺旋ではないが黄金比に近い例として度々挙げられる。工学分野では、自動車ではスポーツカーやオフロード、セミトレーラー用トラクタや軽トラックのトレッド（輪距）とホイールベース（軸距）の関係が黄金比に近い。具体的には 普通乗用車であれば1500 mm 程度のトレッドに対し、ホイールベースが2400 mm 前後とやや短い値となる。これは、いずれの車種においても旋回性能が重要視されるためである。

黄金比は、容姿の美しさの指標として美容業界でもよく用いられ、身体において足底から臍（へそ）までの長さと臍から頭頂までの長さの比が黄金比であれば美しい、また、顔面の構成要素である目、鼻、口などの長さや間隔、細かな形態も黄金比に合致すれば美しいとされている。そして、その黄金比は横1：縦1.618となっている顔である。 なお、黄金比に近い容貌はコーカソイド（白人）に多く、日本人を含むアジア人は黄金比とはかけ離れてることが多いため、日本においてはアジア人に近い「白銀比」（別名「大和比」）という比率で美しさを論じる審美観が存在し、白銀比が古代から現代までの建築、仏像の造形、さらには現代の創作などにおいて「かわいい」キャラクターデザインなど日本の文化の背景の一つになっているという分析もある。

黄金数の小数展開

（テンプレート:OEIS）

参考文献

• テンプレート:Cite book - 注釈：原タイトル：Der Goldene Schnitt. 原著第2版の翻訳
• テンプレート:Cite book - 注釈：原タイトル：Euclidis opera omnia. 世界最初の近代語訳全集
• テンプレート:Cite book
• テンプレート:Cite book - 注釈：著者は500点を超す、古代アッティカの杯の実測調査から「黄金分割」伝説を否定し、新しく星形五角形を基準とする「魔除けの分割」という比例関係を発見。
• テンプレート:Cite book
• テンプレート:Cite book - 注釈：原書名：The golden ratio and Fibonacci numbers.
• テンプレート:Cite book
• テンプレート:Cite book - 注釈：原タイトル：Der Goldene Schnitt. 原著第2版の翻訳
• テンプレート:Cite book
• テンプレート:Cite book - 注釈：原タイトル：The golden ratio.
  • テンプレート:Cite book - 注釈：原タイトル：THE GOLDEN RATIO. 国際ピタゴラス賞及びペアノ賞受賞。
• テンプレート:Citation
• テンプレート:Citation

関連項目

• 黄金角
• 黄金三角形
• 黄金進法
• 黄金分割探索
• 貴金属比
  • 貴金属比#青銅比
  • 白銀比
• 五芒星
• 数学的な美
• 対数螺旋#黄金螺旋
• 美人
• フィボナッチ数
• リュカ数

外部リンク

• テンプレート:高校数学の美しい物語
• テンプレート:Kotobank
• テンプレート:Kotobank
• テンプレート:Kotobank
• テンプレート:MathWorld
• Golden Ratio - Wolfram Alpha
• 黄金比の色々―黄金比を具体例や図形でわかりやすく解説したサイト
• 黄金比φについて（その1）－黄金比とはどのようなものなのか
• 円周率と黄金比