2の平方根

2 の正の平方根 ($\sqrt{2}$) は、隣辺の長さが テンプレート:Math の直角二等辺三角形の斜辺の長さである。

2 の平方根（にのへいほうこん、テンプレート:Lang-en-short）とは、平方して テンプレート:Math になる無理数のことである。すなわち、

$r^2=r\times r=2$

を満たす実数 テンプレート:Mvar のことである。

概説

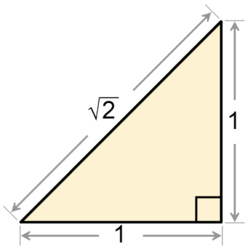
2の平方根は、後述するように無理数である。2 の平方根は、人類の歴史において極めて初期の段階で発見されており、おそらく最初に知られた無理数であると考えられている。幾何学的には、1辺の長さが テンプレート:Math の正方形の対角線の長さに相当する。

テンプレート:Math の平方根には正負の 2 つがある。その内正である方を

$\sqrt{2}$

と書き、「ルート 2」と読む。またこのとき、負の平方根は

$-\sqrt{2}$

と書き表すことができる。

$\sqrt{2}$ は無理数であるから、その小数部分は循環しない。$\sqrt{2}$ の小数点以下 98 桁までは以下の通りである。

$\sqrt{2}$ = 1.414213 562373 095048 801688 724209 698078 569671 875376 948073 176679 737990 732478 462107 038850 387534 327641 57…

上記の最初の数桁を、語呂合わせで「一夜一夜に人見頃（ひと よ ひと よ に ひと み ご ろ）」などと覚える記憶法がしばしば用いられている。

性質

• $\sqrt{2}$ は代数的整数である。$\sqrt{2}$ の有理数体 $\mathbb{Q}$ 上の既約多項式は テンプレート:Math である。
• $\sqrt{2}$ の近似値として テンプレート:Math が挙げられる。
  • 分母・分子が2桁以内のものではこれが $\sqrt{2}$ に最も近い。
• $\sqrt{2}$ の連分数展開は

$\sqrt{2}=1+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{\ddots }}}}}}}$

となる。これはしばしば テンプレート:Math と表記される。連分数展開を途中で打ち切ることで、$\sqrt{2}$ の近似値を計算することができる。

連分数展開による近似

計算回数	近似値	誤差 (%)	計算回数	近似値	誤差 (%)
0	テンプレート:Math	テンプレート:Math	7	テンプレート:Math	テンプレート:Math
1	テンプレート:Math	テンプレート:Math	8	テンプレート:Math	テンプレート:Math
2	テンプレート:Math	テンプレート:Math	9	テンプレート:Math	テンプレート:Math
3	テンプレート:Math	テンプレート:Math	10	テンプレート:Math	テンプレート:Math
4	テンプレート:Math	テンプレート:Math	11	テンプレート:Math	テンプレート:Math
5	テンプレート:Math	テンプレート:Math	12	テンプレート:Math	テンプレート:Math
6	テンプレート:Math	テンプレート:Math	13	テンプレート:Math	テンプレート:Math

歴史

バビロニアの粘土板 YBC 7289（紀元前2000 - 1650年頃）に、テンプレート:Math の平方根の近似が六十進法で 4 桁の精度で与えられている。

$1+\frac{24}{60}+\frac{51}{60^2}+\frac{10}{60^3}=1.41421\overline{296}$

これは十進法では 6 桁の近似精度である。古い時代のうちで精度の高い近似としてほかに、古代インドの数学者によるものが知られており、シュルバ・スートラ（紀元前800 - 200年頃）では、テンプレート:Math の平方根が「基準の長さ (テンプレート:Math) からその三分の一だけ増やし、さらにこの三分の一のそのまた四分の一から、この四分の一の三十四分の一だけ取り去ったものを加える 」として与えられている。これはつまり、

$1+\frac{1}{3}+\frac{1}{3\cdot 4}-\frac{1}{3\cdot 4\cdot 34}=\frac{577}{408}\approx 1.414215686$

を与えていることになる。

無理数はピタゴラス教団のメタポンタムのヒッパソスによって発見されたとされている。通説では、ヒッパソスが無理数を発見したのは テンプレート:Math の平方根を分数として表そうと試みていたときであり、彼は テンプレート:Math の平方根の無理性の（おそらく幾何学的な）証明を与えたといわれている。ところがピタゴラスは（有理）数の絶対性を信じていたため無理数の存在を受け入れることができなかった。ピタゴラスたちはこのような数を｢アロゴン(Alogon，口にできない)｣とよんで研究対象から除外し，そのことを教団外の人たちには秘密にしていたといわれている。ピタゴラスは論理的に無理数の非存在を示すことはできなかったが、その信念から無理数の存在を受け入れることができず、ヒッパソスを溺死の刑に処したとされている。

無理数であることの証明

有理根定理を用いた方法

$\sqrt{2}$ の有理数体 $\mathbb{Q}$ 上の既約多項式 テンプレート:Math を用いる。テンプレート:Math は有理根をもつと仮定する。それを テンプレート:Math（テンプレート:Mvar, テンプレート:Mvar を互いに素な整数）と表すと、有理根定理より、テンプレート:Mvar は定数項 テンプレート:Math の約数、テンプレート:Mvar は最高次係数 テンプレート:Math の約数である。ゆえに テンプレート:Math の根 $\sqrt{2}$ は整数または無理数である。テンプレート:Math は平方数でないから、$\sqrt{2}$ は整数ではない。ゆえに、$\sqrt{2}$ は無理数である。■

この証明は $\sqrt{2}$ に限らず一般化して、平方数でない自然数の平方根の無理性を示すことにも使える。

背理法

背理法（無限降下法）を用いた証明を以下に示す。

$\sqrt{2}$ が有理数であると仮定すると、$\sqrt{2}$ は既約分数で表すことができる。すなわち、互いに素である（公約数を テンプレート:Math 以外に持たない）整数 テンプレート:Mvar, テンプレート:Mvar を用いて テンプレート:NumBlk と表せる。テンプレート:EquationNote の両辺を2乗し分母を払うと テンプレート:NumBlk テンプレート:EquationNote から テンプレート:Math は偶数であり、ここから テンプレート:Mvar は偶数であることを示すことができる。したがって テンプレート:Mvar は整数 テンプレート:Mvar を用いて以下のように表すことができる。 テンプレート:NumBlk テンプレート:EquationNote を テンプレート:EquationNote の式に代入して整理すると以下の関係を得る。 テンプレート:NumBlk テンプレート:EquationNote より テンプレート:Math は偶数なので、テンプレート:Mvar も偶数である。以上より、テンプレート:Mvar, テンプレート:Mvar ともに偶数であることが示されたが、これは テンプレート:Mvar, テンプレート:Mvar が互いに素であるという仮定に矛盾する。ゆえに、$\sqrt{2}$ は無理数であることが示された。■

無限降下法を意識した証明だと、テンプレート:Mvar, テンプレート:Mvar が テンプレート:Mvar, テンプレート:Mvar と同様に偶数であるといえ、テンプレート:EquationNote の右辺が何回でも テンプレート:Math で約分できることになり、矛盾となる。

素因数分解の一意性を用いた方法

素因数分解の一意性（テンプレート:Math より大きな整数の素因数分解は、素数の積の順序を除いて一意である）ことを利用する。

1. $\sqrt{2}$ が有理数であると仮定する。$\sqrt{2}=\frac{a}{b}$ （テンプレート:Mvar, テンプレート:Mvarは互いに素な整数）と表す。（このような分数を既約分数と呼ぶ）。
2. テンプレート:Math は平方数でないため、分母 テンプレート:Mvar は テンプレート:Math ではない。
3. テンプレート:Mvar は互いに素なので、テンプレート:Mvar を割り切り テンプレート:Mvar を割り切れない素数 テンプレート:Mvar が存在する。
4. テンプレート:Mvar の平方 テンプレート:Math の素因数分解は テンプレート:Mvar の素因数をそれぞれ二乗したものになる。
5. 従って素因数の一意性から テンプレート:Math は テンプレート:Math を割り切れない。
6. $\frac{a^2}{b^2}$ は既約分数であり整数ではない。
7. よって $\sqrt{2}$ は有理数ではない。

この証明はある整数の テンプレート:Mvar 乗でない整数の テンプレート:Mvar 乗根が無理数である証明に拡張できる。

背理法を使わない方法

背理法を用いずに証明することができる。ただし、その構想には、背理法による証明過程における、矛盾の発生した点から論理を始めるという点で、直観的ではなく、きわめて形式的である。

平方数の各素因数の個数は偶数個であることと、素因数分解の一意性を用いる。

任意の自然数 テンプレート:Math2 に対して、テンプレート:Math2 の素因数 テンプレート:Math の個数はそれぞれ偶数、奇数である。

ゆえに、素因数分解の一意性により、テンプレート:Math2

∴ $\sqrt{2}\ne \frac{m}{n}$

テンプレート:Math2 の任意性より、テンプレート:Sqrt は無理数である。■

日常生活における2の平方根

白銀長方形（縦 : 横 = テンプレート:Math）

テンプレート:See also テンプレート:Math : $\sqrt{2}$（およそ テンプレート:Math）の比率は用紙サイズ（A3 や A4 など）に採用されている（ISO 216 で標準化されている）他、建物などに使われる。一辺と他辺がこの比となる長方形は、白銀長方形 (テンプレート:En)、またはルート長方形と呼ばれる。

この比が用紙サイズとして用いられている理由は、用紙を長手方向に半分にしたときに元と相似の形状となるため、大きな用紙を切るだけで規格に適合した小さな用紙が得られるためである。この融通性は実用上非常に都合が良い（用紙の縦、横の長さの値は テンプレート:Math など公比を テンプレート:Math とする等比数列としている）。

また、日本建築におけるモジュールの1つとして テンプレート:Math の平方根が用いられていると考えられる。例として法隆寺の五重塔を上から見た投影平面図における辺（短辺と長辺）の関係が挙げられる。大工道具の指矩（さしがね）の裏面には裏目として角目と呼ばれる目盛（$\sqrt{2}$ を掛けたもの）が刻まれているものもある。この利用方法として、丸太から最大の方形角材を製材するときの寸法採りに用いられる。方法として丸太の直径を テンプレート:Math 倍目盛にて計測し、求めた値の裏面に当たる値が最大方形の 1 辺の長さとなる（直角二等辺三角形での辺長関係 = テンプレート:Math）。

テンプレート:Math の小数表示の求め方

テンプレート:Math の小数表示の求め方として、素朴に求めるには、2×100ⁿに近い平方数を探すという方法がある。例えば、200は196(=14²)に近いため10√2=√200≒√196=14より√2≒1.4など。また、2=100/50≒100/49=(10/7)²から√2≒10/7=1.428571...のような2に近い平方数/平方数を探す方法もある。より効率を追究した方法として、開平法がある。これは一般の位取り記数法表示でも可能である。

関連項目

• 冪根
• 平方根
• 3の平方根
• 5の平方根
• 6の平方根
• 7の平方根
• 10の平方根
• 白銀比
• 2の立方根

外部リンク

• 2の平方根の近似値（100万桁）2008年7月12日閲覧