ロジスティック写像

ロジスティック写像の振る舞いをクモの巣図法で示した図。初期値を0.2としてパラメータ（図中の r）を 1 から 4 まで増やしたときに起こる振る舞いの変化がアニメーションで示されている。

ロジスティック写像（ロジスティックしゃぞう、テンプレート:Lang-en）とは、テンプレート:Math2 という2次関数の差分方程式（漸化式）で定められた離散力学系である。単純な2次関数の式でありながら、驚くような複雑な振る舞いを生み出すことで知られる。ロジスティックマップテンプレート:Sfnmや離散型ロジスティック方程式（テンプレート:Lang-en）テンプレート:Sfn、単に2次写像族テンプレート:Sfnテンプレート:Sfnや2次関数族テンプレート:Sfnとも呼ばれる。

ロジスティック写像の テンプレート:Mvar はパラメータと呼ばれる定数、テンプレート:Mvar が変数で、適当に テンプレート:Mvar の値を決め、最初の テンプレート:Math を決めて計算すると、テンプレート:Math という数列が得られる。この数列を力学系分野では軌道と呼び、軌道は テンプレート:Mvar にどのような値を与えるかによって変化する。パラメータ テンプレート:Mvar を変化させると、ロジスティック写像の軌道は、一つの値へ落ち着いたり、いくつかの値を周期的に繰り返したり、カオスと呼ばれる非周期的変動を示したりと様々に変化する。

ロジスティック写像を生物の個体数を表すモデルとして見る立場からは、変数 テンプレート:Mvar は1世代目、2世代目…というように世代ごとに表した個体数を意味しており、ロジスティック写像とは現在の個体数 テンプレート:Mvar から次の世代の個体数 テンプレート:Math を計算する式である。生物個体数モデルとしてのロジスティック写像は、ある生物の個体数がある環境中に生息し、さらにその環境と外部との間で個体の移出入がないような状況を想定しており、テンプレート:Mvar は正確には個体数そのものではなく、その環境中に存在できる最大個体数に対する割合を意味する。微分方程式で個体数をモデリングするロジスティック方程式の離散化からもロジスティック写像は導出でき、「ロジスティック写像」という名もそのことに由来する。

2次関数の力学系としての研究は20世紀初頭からあったが、1970年代、特に数理生物学者ロバート・メイの研究によってロジスティック写像は広く知られるようになった。メイ以外にも、スタニスワフ・ウラムとジョン・フォン・ノイマン、テンプレート:仮リンク、テンプレート:仮リンク、テンプレート:仮リンクら、ミッチェル・ファイゲンバウムなどがロジスティック写像の振る舞い解明に関わる仕事を成している。

定義と背景

単純に言えば、ロジスティック写像とは次のような2次関数であるテンプレート:Sfn。

式中の テンプレート:Mvar は定数を意味し、パラメータと呼ばれるテンプレート:Sfn。テンプレート:Mvar 以外には、テンプレート:Mvar や テンプレート:Mvar や テンプレート:Mvar をパラメータの記号に使うこともあるテンプレート:Sfnm。

式 (テンプレート:EqNoteN) に対して、まず定数 テンプレート:Mvar の具体的な数値を決める。さらに変数 テンプレート:Mvar の値を適当に決め、式から テンプレート:Mvar の値を計算する。そして、得られた テンプレート:Mvar の値を新しい テンプレート:Mvar の値とみなして式に代入し、新しい テンプレート:Mvar の値を計算する。このような計算を繰り返すことが、ロジスティック写像を使って行うことであるテンプレート:Sfn。例として、テンプレート:Mvar を テンプレート:Math、最初の テンプレート:Mvar を テンプレート:Math としたときの繰り返し計算を5回目まで行うと、以下の表のようになるテンプレート:Sfn。

a を 2、最初の x を 0.01 としたときに、ロジスティック写像の計算を繰り返した例テンプレート:Sfn
（小数点以下10桁までで計算）

計算回数	入力する x の値	y = 2x(1 − x) の計算結果
1	0.01	2 × 0.01 × (1 − 0.01) = 0.0198
2	0.0198	2 × 0.0198 × (1 − 0.0198) = 0.03881592
3	0.03881592	2 × 0.03881592 × (1 − 0.03881592) = 0.0746184887
4	0.0746184887	2 × 0.0746184887 × (1 − 0.0746184887) = 0.1381011397
5	0.1381011397	2 × 0.1381011397 × (1 − 0.1381011397) = 0.2380584298

ロジスティック写像自体は中学校で習うような何の変哲もない2次関数であり、計算自体も中学生でも可能であるテンプレート:Sfnm。繰り返しの計算も電卓ででき、コンピュータの表計算ソフトを使えばより簡単にできるテンプレート:Sfn。

ロジスティック写像は、漸化式あるいは差分方程式の形式で次のようにも書き表されるテンプレート:Sfnm。

テンプレート:Math の値を決めると、この差分方程式にしたがい、その後の変数の値 テンプレート:Math2 が順次に計算できるテンプレート:Sfn。このような数列を作る差分方程式を、力学系（ダイナミカルシステム）とも呼ぶテンプレート:Sfn。力学系とは、時間とともに状態が変化する系（システム）のことで、とりわけ現在の状態が決まればその後の状態も一意的に決まる系を指すテンプレート:Sfn。差分方程式 (テンプレート:EqNoteN) のような形式で定義される力学系はとくに離散力学系と呼ばれるテンプレート:Sfn。

力学系的な視点では、変数 テンプレート:Mvar の下付き添え字 テンプレート:Mvar を時刻や時間と呼ぶテンプレート:Sfnm。数列の最初の値 テンプレート:Math は初期値と呼ばれるテンプレート:Sfn。変数の時間変化の様子を、明確な専門用語ではないが振る舞いと呼ぶテンプレート:Sfn。と言っても、時刻 テンプレート:Mvar は物理的な時間を本当に意味しているわけではなく、何かしらの現象の進行を表している便宜的なラベルのようなものであるテンプレート:Sfn。

後で詳述するように、ロジスティック写像は生き物の個体数の変化を考える式として世に広まった側面を持つテンプレート:Sfn。この場合、テンプレート:Mvar は、ある世代における生き物の個体数を、生息環境で可能な最大生息個体数で割った値を意味しているテンプレート:Sfn。差分方程式 (テンプレート:EqNoteN) によって、テンプレート:Mvar 世代目の個体数から テンプレート:Math 世代目の個体数が計算できるというのが、生物個体数モデルとしてのロジスティック写像の意味であるテンプレート:Sfn。個体数が増えていくと、個体数の増加速度は下がってくるだろうから、この効果をロジスティック写像では テンプレート:Math という項で取り入れているテンプレート:Sfn。例えば、ある世代で個体数が最大生息個体数に近くて テンプレート:Math2 だとすれば 項 テンプレート:Math は テンプレート:Math にとても近い数値になるので、次の世代の個体数 テンプレート:Math2 は急激に減ることになるテンプレート:Sfn。

「ロジスティック写像」の名の中に出てくる写像とは、ある集合の要素をまたある集合の要素に対応させる規則を指す用語であるテンプレート:Sfn。関数に似たようなものだが、関数を数以外の集合も扱うような場合も含めてより一般化したのが写像といえる。写像という視点からは、ロジスティック写像は実数の1点を実数の1点へ対応させる規則だといえるテンプレート:Sfnm。ただし、「関数」と「写像」に数学全体で共有されている厳密な呼び分けは存在しておらず、実際のところ、どちらの言葉を使うかは各分野の習慣に依るところが大きい。力学系分野では、式 (テンプレート:EqNoteN) のような差分方程式を写像として捉え、写像という語で呼ぶことが多いテンプレート:Sfnm。

ロジスティック写像を写像の形で表現すると、

や

のように記されるテンプレート:Sfnm。写像がパラメータ テンプレート:Mvar に依存していることを明確にするために、

のように、写像の記号にパラメータ記号の添え字を付けて表すこともあるテンプレート:Sfnm。式 (テンプレート:EqNoteN) や式 (テンプレート:EqNoteN) のような写像としての表現は、式 (テンプレート:EqNoteN) のような差分方程式の表現と実質的に同等だが、時刻 テンプレート:Mvar を一々書き表さなくてもよい利便性もあってしばしば使われるテンプレート:Sfn。

離散力学系の数列 テンプレート:Math2 は、写像 テンプレート:Mvar を繰り返し適用して生み出されるという見方もできるテンプレート:Sfnm。初期値を テンプレート:Math2 とすると、

というように、数列は テンプレート:Math2 に写像を繰り返し適用して作られるものとしても書けるテンプレート:Sfn。このように写像を繰り返し適用する操作を写像の反復などと呼ぶテンプレート:Sfnm。簡単に表記するために、写像の反復を

というように書くテンプレート:Sfn。テンプレート:Math で、テンプレート:Math2 に対する テンプレート:Mvar の テンプレート:Mvar 回反復を意味しているテンプレート:Sfn。そして、差分方程式から生み出される

という列、あるいは写像の反復から生み出される

という列を、力学系では軌道と呼ぶテンプレート:Sfnm。力学系という分野の関心は、与えられた力学系の軌道の振る舞いを研究することにある。

入力と結果が単純な比例関係で結ばれているようなシステムを線形といい、比例関係で表すことができないようなシステムを非線形というテンプレート:Sfn。ロジスティック写像は、考えられる限りでもっとも単純な非線形関数である2次関数で定義されるテンプレート:Sfnm。しかし、その非常に簡単な式とは裏腹に、ロジスティック写像は非常に複雑な振る舞いを生み出すテンプレート:Sfn。2次関数の繰り返し計算という設定が現代的な数学の主題の一つであり、豊饒な数学理論を引き起こすテンプレート:Sfnm。ロジスティック写像には「思いもよらぬ奥深い内容」テンプレート:Sfn「力学系で起こる数多くの最も重要な現象」テンプレート:Sfn、そして「信じられないような複雑な振舞い」テンプレート:Sfnが含まれている。後述するようにロジスティック写像ではカオスという現象が現れ、カオス入門の好適な題材でもあるテンプレート:Sfn。

定義域とグラフ

ロジスティック写像のグラフ（x_n+1 と x_n の関係）。グラフは放物線の形をしており、パラメータ a が変わると放物線の頂点が変わる。

前述のように、ロジスティック写像には生物の個体数の変動を考えるモデルとしての側面がある。このとき、ロジスティック写像の変数 テンプレート:Mvar は生物の個体数を最大生息数で割った値であったから、テンプレート:Mvar が取り得る数値は テンプレート:Math の間に限られるテンプレート:Sfn。そういった事情もあり、ロジスティック写像の変数の範囲を区間 テンプレート:Closed-closed に限って、その振る舞いが議論されることが多いテンプレート:Sfnm。

変数を常に テンプレート:Math に限定しようとすると、必然的にパラメータ テンプレート:Mvar が取れる範囲は テンプレート:Math から テンプレート:Math まで テンプレート:Math に限定されるテンプレート:Sfn。なぜならば、テンプレート:Math が テンプレート:Closed-closed の範囲内にあれば、テンプレート:Math の最大値は テンプレート:Math となっているテンプレート:Sfn。したがって、テンプレート:Math では テンプレート:Math2 の値が テンプレート:Math を超える可能性が出て来てしまうテンプレート:Sfn。一方、テンプレート:Mvar が負のときは、テンプレート:Mvar が負の値を取るようになってしまう。

写像のグラフを利用することで、その振る舞いの多くを知ることもできるテンプレート:Sfnm。ロジスティック写像 テンプレート:Math2 のグラフとは、横軸を テンプレート:Math（あるいは テンプレート:Mvar）とし、縦軸を テンプレート:Math（あるいは テンプレート:Math）として、平面上に テンプレート:Math と テンプレート:Math の関係を示した曲線であるテンプレート:Sfn。ロジスティック写像のグラフは、テンプレート:Math の場合を除き、

を頂点とする放物線の形をしているテンプレート:Sfnm。テンプレート:Mvar を変化させると頂点は上下に動き、放物線は形を変えるテンプレート:Sfn。また、ロジスティック写像の放物線は横軸（テンプレート:Math2 の直線）と2点で交わるテンプレート:Sfn。テンプレート:Math2 と テンプレート:Math2 がその2つの交点で、これらの交点の位置は テンプレート:Mvar の値に影響されず一定であるテンプレート:Sfn。

ロジスティック写像のグラフ上で、クモの巣図法によった軌道を描いた例。また、グラフ上の不動点 x_f 1, x_f 2 の位置。

写像のグラフは、とくにロジスティック写像のような1変数の写像のグラフは、その写像の振る舞いを理解するための鍵であるテンプレート:Sfn。グラフの効能の一つは、不動点と呼ばれる点の図示であるテンプレート:Sfn。写像のグラフに重ねるように テンプレート:Math の直線（45°の直線）を引く。この45°直線とグラフが交わる点があれば、その点が不動点であるテンプレート:Sfnm。式で書くと、不動点とは

を満たしている点であり、写像を適用しても変化しない点を意味するテンプレート:Sfnm。不動点を テンプレート:Math と表記することにする。ロジスティック写像の場合に式 (テンプレート:EqNoteN) を満たす不動点は、テンプレート:Math を解いて、

の2点である（テンプレート:Math の場合を除く）テンプレート:Sfnm。不動点の概念は離散力学系において最も重要となるテンプレート:Sfn。

1変数写像に対して使えるもう一つのグラフを利用した技術が、クモの巣図法と呼ばれる手法であるテンプレート:Sfn。横軸上に初期値 テンプレート:Math を決めた後に、そこから テンプレート:Math の曲線まで縦向きに直線を引く。テンプレート:Math の曲線にぶつかったところから テンプレート:Math の45°直線まで横向きに直線を引き、45°直線にぶつかったところから テンプレート:Math の曲線まで縦向きに直線を引く。これを繰り返すことで、平面上にクモの巣状ないし階段状の図ができるテンプレート:Sfn。実はこの作図は図示的に軌道の計算を行ってることに等しく、作成されたクモの巣状の図は テンプレート:Math から出発する軌道を表しているテンプレート:Sfn。この図法によって、軌道の全体的な振る舞いを一目で見ることができるテンプレート:Sfn。

振る舞い、パラメータ a による変化

ロジスティック写像のパラメータ（図中では r）を 0.02 から 4 まで変化させたときの振る舞いの変化を示したアニメーション。横軸が繰り返し数 n（図中では t）、縦軸が x で、繰り返し計算 200 回までの x を図示している。

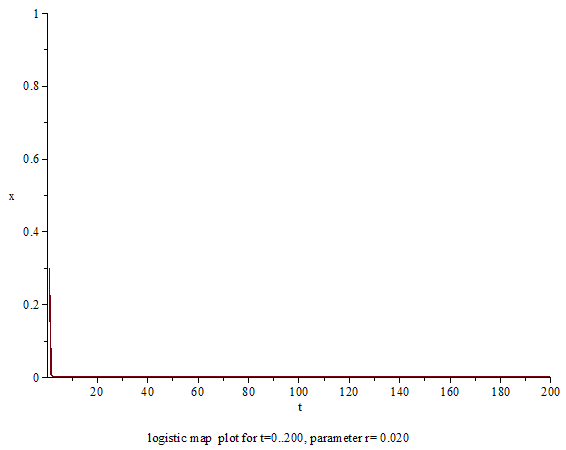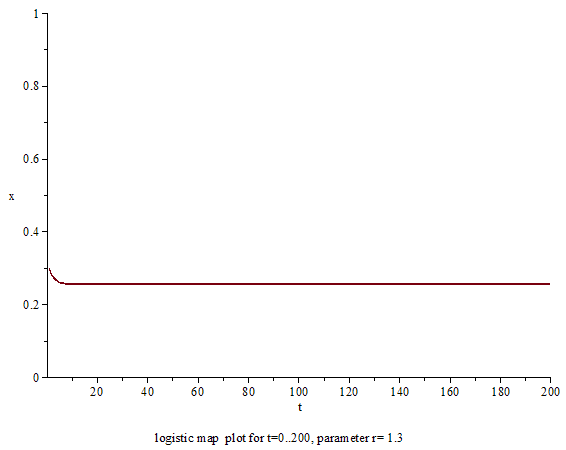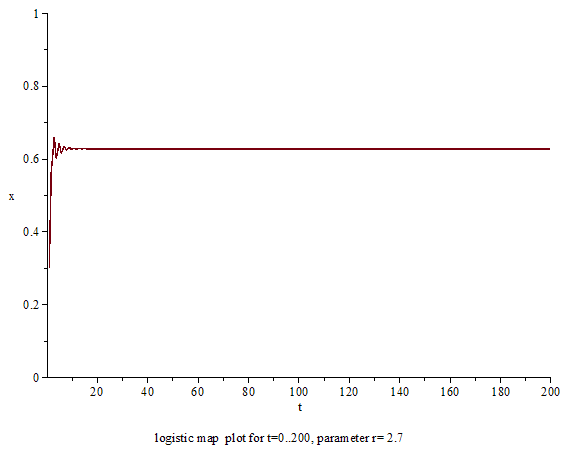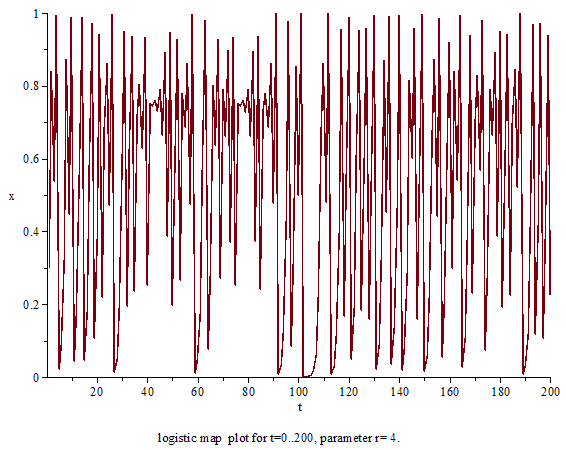
上述のように、ロジスティック写像自体は何の変哲もない2次関数であり、軌道の計算自体も中学生でも可能であるテンプレート:Sfnm。力学系的に重要な問題は、パラーメータ テンプレート:Mvar を変化させると軌道の振る舞いがどう変わるのかにあるテンプレート:Sfn。テンプレート:Mvar の数値によって、ロジスティック写像の軌道の振る舞いは単純にも複雑にも変わるテンプレート:Sfn。以下、テンプレート:Mvar を増やしていったときに、ロジスティック写像の振る舞いがどのように変化していくかを順に説明する。

0 ≤ a < 1 のとき

まず、パラメータが テンプレート:Math2 のときは、初期値 テンプレート:Math がどんな値であろうが、テンプレート:Math となるテンプレート:Sfn。つまり、テンプレート:Math2 におけるロジスティック写像の軌道は、初期値以降の値が全て テンプレート:Math となるような軌道で、この場合あまり調べる中身はないテンプレート:Sfn。

次に、パラメータが テンプレート:Math2 の範囲にあるとき、初期値 テンプレート:Math が テンプレート:Math から テンプレート:Math までのどんな数値であったとしても、テンプレート:Mvar は単調に減少していくテンプレート:Sfn。つまり、テンプレート:Math2 の極限で テンプレート:Mvar は テンプレート:Math へ収束するテンプレート:Sfn。この収束先の テンプレート:Math2 という点は、式 (テンプレート:EqNoteN) で示した不動点 テンプレート:Math であるテンプレート:Sfn。このように周りの軌道が収束するタイプの不動点は、漸近安定、安定、あるいは吸引的と呼ばれるテンプレート:Sfnm。逆に時間 テンプレート:Mvar の増加と共に テンプレート:Math の近くの軌道が テンプレート:Math から離れていくならば、その不動点 テンプレート:Math は不安定や反発的と呼ばれるテンプレート:Sfnm。

パラメータ a = 0.9 のクモの巣図（左）と時系列（n と x_n の関係）の図（右）。軌道は 0 に向かって単調減少で収束する。

不動点が漸近安定かどうかを知るには、写像 テンプレート:Mvar の微分を求めるという一般的で簡単な方法があるテンプレート:Sfn。テンプレート:Math の微分 テンプレート:Math2 を テンプレート:Math と表すとする。 この微分が不動点 テンプレート:Mvar で

という条件を満たせば、テンプレート:Mvar は漸近安定であるテンプレート:Sfn。ここで、テンプレート:Abs は 〇 の絶対値を意味する。

漸近安定な不動点（左）と不安定な不動点（右）の接線傾きと周囲の軌道の様子

写像のグラフでこのことを見ると、グラフの曲線上の点 テンプレート:Mvar における接線の傾きが テンプレート:Math から テンプレート:Math の間にあれば、テンプレート:Mvar は安定で、その周囲の軌道は テンプレート:Mvar へ引き寄せられるということであるテンプレート:Sfn。ロジスティック写像の微分は、

なので、テンプレート:Math かつ テンプレート:Math2 では テンプレート:Math2 であるから、不動点 テンプレート:Math2 は式 (テンプレート:EqNoteN) を満たしているテンプレート:Sfn。

ただし、式 (テンプレート:EqNoteN) による判別法は、テンプレート:Mvar からどのぐらいの範囲にある軌道が テンプレート:Mvar へ引き寄せられるかは分からないテンプレート:Sfn。あくまでも、テンプレート:Mvar のある近傍内の テンプレート:Mvar が収束することを保証しているだけであるテンプレート:Sfn。今の場合、テンプレート:Math へ収束する初期値の領域は テンプレート:Closed-closed 全域であるが、これを明確に知るには別の考察を要するテンプレート:Sfn。

不動点が不安定かどうかの判別方法は、同じように写像の微分から分かるテンプレート:Sfn。ある不動点 テンプレート:Mvar が

を満たすとき、テンプレート:Mvar は不安定であるテンプレート:Sfn。パラメータが テンプレート:Math2 の範囲にあるときには、もう一方の不動点 テンプレート:Math2 は負の値であるため テンプレート:Closed-closed の範囲には現れないが、不安定な不動点として存在しているテンプレート:Sfn。

1 ≤ a ≤ 2 のとき

パラメータがちょうど テンプレート:Math のとき、ロジスティック写像の軌道はこれまでと同様に テンプレート:Math へ収束するテンプレート:Sfn。ただし、収束する速さが、テンプレート:Math ではゆっくりになるテンプレート:Sfn。テンプレート:Math における不動点 テンプレート:Math は漸近安定ではあるが、式 (テンプレート:EqNoteN) を満たしていないテンプレート:Sfn。実のところ、式 (テンプレート:EqNoteN) による判別法は写像を不動点近傍で1次近似することによって成り立っているテンプレート:Sfn。テンプレート:Math ではこの近似が成り立たなくなり、安定・不安定は写像の2次（2乗）の項によって決まるようになるテンプレート:Sfn。

テンプレート:Math の状態をグラフで見ると、テンプレート:Math でグラフの曲線が45°対角線にちょうど接した状態になっているテンプレート:Sfn。このとき、テンプレート:Math2 の範囲では負の範囲に存在していた不動点 テンプレート:Math2 の値は、テンプレート:Math2 となっているテンプレート:Sfn。つまり、テンプレート:Mvar が増えるにつれて テンプレート:Math2 の値は テンプレート:Math へと近づいていき、ちょうど テンプレート:Math で、テンプレート:Math2 は テンプレート:Math2 と衝突するテンプレート:Sfn。この衝突によってトランスクリティカル分岐という現象が起こるテンプレート:Sfn。

a = 1 で起こるロジスティック写像のトランスクリティカル分岐の様子。a < 1 では x_f 2 が不安定な不動点として [0, 1] の外に存在しているが、a = 1 で2つの不動点が衝突し、a > 1 では x_f 2 が安定な不動点として [0, 1] の間に現れる。

分岐とは力学系の振る舞いが定性的に変わる現象を指す用語で、この場合のトランスクリティカル分岐では、不動点同士で安定性の交替が起きるテンプレート:Sfn。つまり、テンプレート:Mvar が テンプレート:Math 未満では テンプレート:Math2 は安定、テンプレート:Math2 は不安定であたったが、テンプレート:Mvar が テンプレート:Math を超えると テンプレート:Math2 は不安定、テンプレート:Math2 は安定になるテンプレート:Sfn。分岐が起きるときのパラメータの値は分岐点と呼ばれるテンプレート:Sfn。ここでは、テンプレート:Math が分岐点であるテンプレート:Sfn。

分岐の結果、ロジスティック写像の軌道は テンプレート:Math2 ではなく、テンプレート:Math2 へ収束するようになるテンプレート:Sfnm。詳しく言えば、パラメータ テンプレート:Math であれば、テンプレート:Math と テンプレート:Math を除く区間 テンプレート:Open-open 上の値から出発する軌道は、単調増加あるいは単調減少しながら テンプレート:Math2 に収束するテンプレート:Sfnm。収束の仕方の違いは、初期値がどの範囲にあるかに依るテンプレート:Sfn。テンプレート:Math では単調増加で収束し、テンプレート:Math では単調減少で収束し、テンプレート:Math では最初の1ステップを除いて単調増加で収束するテンプレート:Sfn。

テンプレート:Multiple image

また、分岐によって不動点 テンプレート:Math2 は不安定化するが、テンプレート:Math 以降も不動点として存在し続けるテンプレート:Sfn。この不安定不動点 テンプレート:Math2 にたどり着く初期値が、テンプレート:Math2 自身以外に存在しないわけではないテンプレート:Sfn。それが テンプレート:Math で、テンプレート:Mvar の値にかかわらずロジスティック写像は テンプレート:Math2 を満たすので、テンプレート:Math に写像を1回適用すると テンプレート:Math2 に写るテンプレート:Sfn。この テンプレート:Math のように、有限回の写像の反復で不動点に直接行き着くような点は最終的不動点などと呼ばれるテンプレート:Sfn。

2 < a < 3 のとき

a = 2.8 におけるクモの巣図法のアニメーション。不動点の周りを回りながら収束していく。

パラメータが テンプレート:Math のときは、初期値 テンプレート:Math と テンプレート:Math を除いて、テンプレート:Math のときと同様に不動点 テンプレート:Math2 に収束するテンプレート:Sfn。ただし、この場合は単調に収束するわけではないテンプレート:Sfn。変数が テンプレート:Math2 にある程度近づくと、変数は テンプレート:Math2 よりも大きくなったり小さくなったりを繰り返し、テンプレート:Math2 の周りで振動しながら収束していくような軌道を示すテンプレート:Sfn。

軌道の不動点周りでの振動は、次のような範囲を行き来する。このパラメータ範囲では、テンプレート:Math2 は区間 テンプレート:Open-open 内に存在するテンプレート:Sfn。写像を一回適用すると テンプレート:Math に写る値を テンプレート:Math と表記するとする。すなわち、テンプレート:Math2 という関係であるテンプレート:Sfnm。変数が区間 テンプレート:Open-open に入ったとき、軌道の不動点周りでの振動が起こり出すテンプレート:Sfn。テンプレート:Open-open は テンプレート:Open-closed へ写され、 テンプレート:Open-closed は テンプレート:Closed-open の中へ写され、…といった具合に振動するテンプレート:Sfnm。

一般的に、分岐の様子を理解するのには分岐図が役に立つテンプレート:Sfn。この図は不動点（または後述の周期点）テンプレート:Mvar をパラメータ テンプレート:Mvar の関数として表したグラフで、横軸に テンプレート:Mvar の値を取り、縦軸に テンプレート:Mvar の値を取って図示するテンプレート:Sfn。 安定な不動点と不安定な不動点を区別するために、前者の曲線は実線で示し、後者の曲線は点線で示したりするテンプレート:Sfn。ロジスティック写像の分岐図を書くと、不動点 テンプレート:Math2 を表す直線と不動点 テンプレート:Math2 を表す曲線が テンプレート:Math で交わり、安定性が入れ替わる様子がわかるテンプレート:Sfn。

パラメータ 0 から 3 までのロジスティック写像の分岐図。青線が不動点 x_f 1 = 0 を表し、赤線が不動点 x_f 2 = 1 − テンプレート:Sfrac を表す。

3 ≤ a < 3.44949… のとき

パラメータがちょうど テンプレート:Math のときも、軌道は不動点 テンプレート:Math2 に収束するテンプレート:Sfn。しかし、テンプレート:Math2 のときよりも変数が収束する速さは遅いテンプレート:Sfn。テンプレート:Math では、微分係数 テンプレート:Math2 は テンプレート:Math に達し、式 (テンプレート:EqNoteN) を満たさなくなっているテンプレート:Sfn。テンプレート:Mvar が テンプレート:Math を過ぎると、テンプレート:Math2 となり、テンプレート:Math2 は不安定な不動点になるテンプレート:Sfn。すなわち、テンプレート:Math でまた分岐が起こるテンプレート:Sfn。

テンプレート:Math では、周期倍化分岐と呼ばれる種類の分岐が起こるテンプレート:Sfn。テンプレート:Math からは、軌道は1点に収束しなくなり、十分に時間 テンプレート:Mvar が進んだ後でも大きい値と小さい値を交互に取り続けるような振る舞いに変わるテンプレート:Sfn。例えば テンプレート:Math2 であれば、変数は テンプレート:Math と テンプレート:Math という2つの値を交互に取り続けるテンプレート:Sfn。

テンプレート:Multiple image

このように同じ値を周期的に巡り続ける軌道を周期軌道と呼ぶテンプレート:Sfn。今の場合、テンプレート:Math2 における変数の最終的な振る舞いは2周期の周期軌道であるテンプレート:Sfn。周期軌道を構成する一つ一つの値（点）を周期点と呼ぶテンプレート:Sfn。テンプレート:Math2 の例で言えば、テンプレート:Math と テンプレート:Math がそれぞれ周期点であるテンプレート:Sfn。ある テンプレート:Mvar が周期点だとすると、2周期点の場合は テンプレート:Mvar に写像を2回適用すると元に戻るので、

という関係が成り立つテンプレート:Sfn。この式にロジスティック写像の式 (テンプレート:EqNoteN) を適用すると、

という4次方程式が得られるテンプレート:Sfnm。この方程式の解が周期点であるテンプレート:Sfnm。実は不動点 テンプレート:Math2 と不動点 テンプレート:Math2 もまた、式 (テンプレート:EqNoteN) を満たすテンプレート:Sfn。したがって、式 (テンプレート:EqNoteN) の解の内、2つの解は テンプレート:Math2 と テンプレート:Math2 に相当し、残り2つの解が2周期点であるテンプレート:Sfn。2周期点をそれぞれ テンプレート:Math2 と表すとする。式 (テンプレート:EqNoteN) を解くことで、テンプレート:Math2 を次のように得られるテンプレート:Sfnm。

不動点の安定性と同じようなことが、周期点についても言えるテンプレート:Sfn。つまり、周囲の軌道を引き付ける周期点は漸近安定な周期点と呼ばれ、周囲の軌道が離れていく周期点は不安定な周期点と呼ばれるテンプレート:Sfn。周期点の安定性判別も、不動点と同じように可能であるテンプレート:Sfn。一般的な場合を想定して、写像を テンプレート:Mvar 回反復させた テンプレート:Math について考える。この微分 テンプレート:Math を テンプレート:Math と表すとする。ある テンプレート:Mvar-周期点 テンプレート:Math2 が

を満たせば、テンプレート:Math2 は漸近安定であるテンプレート:Sfn。不安定についても不動点と同じように

を満たせば、テンプレート:Math2 は不安定であるテンプレート:Sfn。

以上の周期点の安定性の議論も、不動点と同じようにグラフ描写によって理解しやすくなるテンプレート:Sfn。この図では、横軸 テンプレート:Mvar に対して縦軸を テンプレート:Math とし、テンプレート:Math と テンプレート:Mvar の関係を表す曲線を描くテンプレート:Sfn。この曲線と45°直線の交点は式 (テンプレート:EqNoteN) を満たす点であるから、交点は不動点と2周期点を表しているテンプレート:Sfn。ロジスティック写像の テンプレート:Math のグラフを描くと、不動点 テンプレート:Math での接線の傾きは テンプレート:Math を境に 1 を超えて不安定化するのが観察できるテンプレート:Sfn。同時に新たな2つの交点が現れ、これらが周期点 テンプレート:Math2 と テンプレート:Math2 であるテンプレート:Sfn。

テンプレート:Multiple image

2周期点の微分係数をロジスティック写像について実際に計算すると、

となるテンプレート:Sfn。これを式 (テンプレート:EqNoteN) に当てはめると、パラメータ テンプレート:Mvar が、

を満たすときに2周期点が漸近安定であることがわかるテンプレート:Sfn。この範囲は テンプレート:Math2 となり、つまり テンプレート:Mvar が テンプレート:Math2 を超えると、2周期点は漸近安定ではなくなり、また振る舞いが変わるテンプレート:Sfn。

テンプレート:Closed-closed 内のほぼ全ての初期値が2周期点に引き寄せられるが、 テンプレート:Math2 と テンプレート:Math2 も テンプレート:Closed-closed 内に不安定な不動点として残り続けているテンプレート:Sfn。これら不安定不動点は、以後 テンプレート:Mvar を増やし続けても テンプレート:Closed-closed 内にずっと残り続けるテンプレート:Sfn。そのため、初期値がちょうど テンプレート:Math2 または テンプレート:Math2 であるときは、軌道は2周期点には引き寄せられないテンプレート:Sfn。さらに、初期値が テンプレート:Math2 に対する最終的不動点である場合と、テンプレート:Math2 に対する最終的不動点である場合も、軌道は2周期点には引き寄せられないテンプレート:Sfn。このような最終的不動点である点は テンプレート:Closed-closed の中に無限に存在するテンプレート:Sfn。しかし、このような点の数は、テンプレート:Closed-closed という実数の集合と比較すれば無視できるほど小さいテンプレート:Sfn。

3.44949… ≤ a ≤ 3.56994… のとき

パラメータ テンプレート:Mvar が テンプレート:Math2 を超えると、それまで安定だった2周期点が不安定になり、安定な4周期点が新たに生まれ、軌道は4周期の振動に引き寄せられるようになるテンプレート:Sfnm。つまり、テンプレート:Math2 でまた周期倍化分岐が起こるテンプレート:Sfn。4周期点における テンプレート:Mvar の値も

を満たすので、この式を解けば4周期点の テンプレート:Mvar の値を求めることができるテンプレート:Sfn。ただし、式 (テンプレート:EqNoteN) は16次方程式であり、不動点と2周期点の4つの解をくくり出したとしても12次方程式であるテンプレート:Sfn。そのため、もはやこれを解いて、2周期点と同じように4周期点の値を表す テンプレート:Mvar の陽関数を得ることはできないテンプレート:Sfn。

256周期までの分岐点の例テンプレート:Sfn

k 番目の分岐	周期 2k	分岐点 ak
1	2	3.0000000
2	4	3.4494896
3	8	3.5440903
4	16	3.5644073
5	32	3.5687594
6	64	3.5696916
7	128	3.5698913
8	256	3.5699340

さらに テンプレート:Mvar が大きくなると、安定な4周期点はまた周期倍化分岐を起こし、安定な8周期点が生まれるテンプレート:Sfn。以降、テンプレート:Mvar が増えるにつれて、16周期、32周期、64周期、…と周期倍化分岐が無限に起こり続け、最終的には無限周期すなわち永遠に元の値に戻ることがない軌道となるテンプレート:Sfn。この周期倍化分岐の無限の系列はカスケードと呼ばれるテンプレート:Sfn。この周期倍化分岐は無限に起こるが、一方で、周期倍化分岐が発生する テンプレート:Mvar の間隔は等比数列的に減少していくテンプレート:Sfn。そのため、パラメータ テンプレート:Mvar がある有限の値に達するまでに、周期倍化分岐の無限回の発生が起きるテンプレート:Sfn。テンプレート:Math で起きた1周期から2周期への分岐を1番目の周期倍化分岐として数えるとする。すると、この周期倍化分岐のカスケードの中では、テンプレート:Mvar 番目の分岐点で安定な テンプレート:Math 周期点が発生する。テンプレート:Mvar 番目の分岐点 テンプレート:Mvar を テンプレート:Math と表すとする。このとき、テンプレート:Math で テンプレート:Math は次のような値に収束することが知られているテンプレート:Sfn。

さらに、テンプレート:Mvar の減少の割合の極限は次式で示すような定数値となることが知られているテンプレート:Sfn。

この テンプレート:Mvar の値は、数理物理学者のミッチェル・ファイゲンバウムにより発見されたことからファイゲンバウム定数と呼ばれるテンプレート:Sfn。テンプレート:Math はファイゲンバウム点と呼ばれるテンプレート:Sfn。周期倍化カスケードの過程では、テンプレート:Mvar と テンプレート:Math は適当なスケール変換によって局所的に全く一致する性質を持つテンプレート:Sfnm。この自己相似性を利用した繰り込みと呼ばれる手法により、ファイゲンバウム定数は求められるテンプレート:Sfnm。以上のようなロジスティック写像が周期倍化カスケードの過程で見せる性質は、後述のように、より広いクラスの写像でも普遍的に現れるテンプレート:Sfn。

あるパラメータに対して軌道が落ち着く最終的な振る舞いを一望するには、近似的な分岐図である軌道図が有用であるテンプレート:Sfnm。この図では、分岐図と同じように横軸にパラメータ テンプレート:Mvar を取り、縦軸に変数 テンプレート:Mvar を取るテンプレート:Sfnm。コンピュータなどを使い、パラメータを決めて、例えば500回反復計算を行うテンプレート:Sfn。そして、計算結果の最初の100回を無視して残りの400回の結果のみを図示するテンプレート:Sfn。これによって、初期の過渡的な振る舞いは無視でき、軌道の漸近的な挙動が残るテンプレート:Sfn。例えば、ある テンプレート:Mvar に対して1点プロットされるときは、それは不動点であり、ある テンプレート:Mvar に対して テンプレート:Mvar 点プロットされるときは、それは テンプレート:Mvar 周期軌道に相当するテンプレート:Sfn。ロジスティック写像に対して軌道図を書くと、安定な周期軌道を表す枝が分裂していく様子が見て取れ、これが周期倍化分岐のカスケードを表しているテンプレート:Sfn。

パラメータ a₁ = 3 から a_∞ = 3.56994… の間で起こる周期倍分岐カスケードの軌道図。64周期（a₅）以降は間隔が非常に狭くなり、ほとんどつぶれている。

パラメータがちょうど周期倍化カスケードの集積点 テンプレート:Math であるとき、変数 テンプレート:Mvar は永遠に閉じることのない非周期軌道へ引き付けられるテンプレート:Sfn。言い換えると、テンプレート:Math では無限周期の周期点が存在しているテンプレート:Sfn。この非周期軌道はファイゲンバウム・アトラクタテンプレート:Sfnmや臨界2^∞アトラクタテンプレート:Sfnmと呼ばれる。アトラクタとは、周りの軌道を引き付けるような性質をもった領域を指す用語で、引き込まれて最終的に続く軌道のことであるテンプレート:Sfnm。これまで述べてきた吸引的な不動点や周期点もアトラクタの仲間であるテンプレート:Sfn。

ファイゲンバウム・アトラクタの構造は、カントール集合というフラクタル図形と同じ構造になっているテンプレート:Sfnm。ファイゲンバウム・アトラクタを構成する点は、無限個でなおかつその濃度は実数と等しいテンプレート:Sfn。一方で、構成する点のどの2つを選んでも、その間に不安定な周期点が必ず存在し、点の分布は連続ではないテンプレート:Sfn。また、ファイゲンバウム・アトラクタのフラクタル次元は、ハウスドルフ次元あるいは容量次元でおよそ 0.54 であることが知られているテンプレート:Sfnm。

カントール集合の構成例。線分の真ん中3分の1を無限に除去し続けると、長さは 0 で何も残らないように見えて、点の数は非可算無限で、それぞれの点のどれだけ小さい近傍の中にも他の点が無限に含まれる、という図形ができるテンプレート:Sfn。

3.56994… < a < 4 のとき

カオスの出現

テンプレート:Multiple image

パラメータ テンプレート:Mvar が テンプレート:Math を超えると、ロジスティック写像はカオスと呼ばれる振る舞いを示すテンプレート:Sfn。カオスとは、大雑把に言えば、ロジスティック写像を表す差分方程式のように確率的な曖昧さがなく次の状態が完全に一意に決まるにもかかわらず起こる複雑で不規則な振る舞いのことであるテンプレート:Sfn。ロジスティック写像の テンプレート:Math の範囲はカオス領域と呼ばれるテンプレート:Sfnm。

カオスが持つ本質の一つが、バタフライ効果という言葉で象徴される予測不可能性であるテンプレート:Sfn。これは、カオスによって初期の状態のわずかな違いが後の状態に巨大な差をもたらすという性質に起因するテンプレート:Sfn。離散力学系で言えば、2つの初期値 テンプレート:Math と テンプレート:Math がどれだけ近い値だとしても、時間 テンプレート:Mvar がある程度進めば、それぞれの行先 テンプレート:Mvar と テンプレート:Math は著しく離れてしまうテンプレート:Sfn。例えば テンプレート:Math を使い、テンプレート:Math2 と テンプレート:Math というきわめて近い2つの初期値でそれぞれの軌道を計算すると、その差は、反復29回を過ぎたころから図上ではっきりわかるほど巨視的な違いに成長するテンプレート:Sfn。

以上のような初期値鋭敏性と呼ばれるカオスの性質は、リアプノフ指数によって定量的に表される。1次元写像の場合、リアプノフ指数 テンプレート:Mvar は次のように計算できるテンプレート:Sfn。

ここで、テンプレート:Math は自然対数を意味する。この テンプレート:Mvar は2つの軌道の距離（テンプレート:Mvar と テンプレート:Math の距離）が指数関数的にどのぐらいの速さで離れていくか意味する指標で、テンプレート:Mvar の値が正ならば初期値鋭敏性を持つ系であること意味し、零または負ならば初期値鋭敏性のないことを意味するテンプレート:Sfn。実際にロジスティック写像の テンプレート:Mvar を数値的に計算すると、テンプレート:Math2 の範囲では テンプレート:Mvar は零または負の値の範囲に留まっており、テンプレート:Math2 の範囲から テンプレート:Mvar が正の値も取るようになることが確認できるテンプレート:Sfn。

窓、間欠性

パラメータが テンプレート:Math を超えてからも、振る舞いのパラメータ テンプレート:Mvar への依存の仕方は単純ではないテンプレート:Sfn。テンプレート:Math のカオス領域には、多くの精巧な数学的構造が潜んでいるテンプレート:Sfn。この領域では、ずっとカオスが続くというわけではなく、安定な周期軌道も再び現れるテンプレート:Sfn。テンプレート:Math での振る舞いは、大きく分けると以下の2種類に分かれるテンプレート:Sfn。

• 安定な周期点。この場合、リアプノフ指数は負を示す。
• 非周期的軌道。この場合、リアプノフ指数は正を示す。

テンプレート:Math の中に存在する安定周期点の領域は周期窓あるいは単に窓と呼ばれるテンプレート:Sfnm。カオス領域を軌道図で見ると、非周期的軌道の領域は無数の点でできた雲のような見た目を示し、その雲に囲まれて点在する空白部分が窓であるテンプレート:Sfn。

a = 3.55 から a = 4 までのロジスティック写像の軌道図（図中では パラメータが r 表記）

各窓では、テンプレート:Math2 よりも前で起きた周期倍化分岐のカスケードが再び起きるテンプレート:Sfn。ただし、それらの周期は前のような テンプレート:Math の安定周期軌道ではなく、テンプレート:Math や テンプレート:Math のような新しい安定周期軌道が生成されるテンプレート:Sfn。最初は テンプレート:Mvar 周期で、そこから周期倍化カスケードが起こる窓は周期 テンプレート:Mvar の窓などと呼ばれるテンプレート:Sfn。例えば、周期3の窓は テンプレート:Math2 辺りの領域に存在しており、この領域内では テンプレート:Math2 という風に周期が倍化していくテンプレート:Sfn。

a = 3.8285 で起きる過渡カオスの様子。3周期軌道に吸引されるまでカオス的に振る舞う。

窓の領域では、カオスは消えておらず背後に存在しているテンプレート:Sfn。しかし、このカオスは不安定であるため、安定な周期軌道のみが観測されるテンプレート:Sfn。窓の領域では、軌道が初期値から安定周期軌道に吸引されるまでに、この潜在的なカオスが現れるテンプレート:Sfn。このようなカオスを過渡カオスと呼ぶテンプレート:Sfn。このようにカオスが潜在的に存在している点において、窓は テンプレート:Math より前で現れた周期軌道とは異なるテンプレート:Sfn。

窓の数は、テンプレート:Math の範囲に無限個あるテンプレート:Sfn。それらの窓の周期は様々で、テンプレート:Math 以上の全ての自然数に対応する周期の窓が存在するテンプレート:Sfn。しかし、各周期の窓がそれぞれ1回ずつ発生するわけではないテンプレート:Sfn。テンプレート:Mvar の値が大きいほどその周期の窓は多く繰り返し発生するテンプレート:Sfn。周期3の窓は1回きりで、例えば周期13の窓は315 回発生するテンプレート:Sfn。その周期3の窓で3周期軌道が生じるとシャルコフスキー順序が完成し、全ての周期の軌道がそれで一通り出現し終える。

テンプレート:Mvar が素数の場合に限定すると、周期 テンプレート:Mvar の窓の個数は

という式で計算できるテンプレート:Sfn。この式は テンプレート:Mvar を素数に限定して導出されたものだが、実際のところ、素数でない テンプレート:Mvar の安定 テンプレート:Mvar 周期点の数についても良い精度で計算できるテンプレート:Sfn。

窓の幅（窓が始まる テンプレート:Mvar と窓が終わる テンプレート:Mvar の差）は、周期3の窓が最も広く、周期が大きいほど幅は狭まっていくテンプレート:Sfn。例えば、周期13の窓の幅は テンプレート:Math2 程度であるテンプレート:Sfn。概算によると、テンプレート:Closed-closed の内のおよそ テンプレート:Math が窓の領域で、残りがカオス軌道が支配する領域となっているテンプレート:Sfnm。

テンプレート:Mvar を増やしていくときに起こるカオスから窓への変化は、接線分岐と呼ばれる分岐によって引き起こされるテンプレート:Sfn。これは、写像の曲線が テンプレート:Math2 の対角線に分岐の瞬間にちょうど接し、さらにパラメータを変化させると曲線と直線が交わって2つの不動点を持つようになる分岐であるテンプレート:Sfn。周期 テンプレート:Mvar の窓であれば、反復写像 テンプレート:Math が接線分岐を起こすことによって安定な テンプレート:Mvar 周期軌道が生まれるテンプレート:Sfn。周期3の窓の接線分岐については正確な分岐点の値が知られており、この分岐点 テンプレート:Mvar の値を テンプレート:Math とすると、テンプレート:Math2 であるテンプレート:Sfn。この分岐の概要は、テンプレート:Math のグラフ（縦軸 テンプレート:Math2・横軸 テンプレート:Mvar のグラフ）を考察することで理解できるテンプレート:Sfn。

テンプレート:Multiple image

この分岐点 テンプレート:Math よりもわずかに小さい テンプレート:Math のときの テンプレート:Math 振る舞いを見てみると、不規則変化に加えて、ほぼ3周期で周期的変化する振る舞いも存在しており、これらが交互に発生する様子が確認されるテンプレート:Sfn。このような周期的振る舞い部分はラミナーと呼ばれ、不規則振る舞い部分はバーストと呼ばれるテンプレート:Sfnm。バーストとラミナーの時間帯の長さに規則性は無く、不規則に変化するテンプレート:Sfn。しかし、より テンプレート:Math に近い テンプレート:Math という値で振る舞いを観察すると、テンプレート:Math のときよりラミナーの平均的な時間長さが長くなり、バーストの平均的な時間長さが短くなるテンプレート:Sfn。さらに テンプレート:Mvar を大きくしていくとラミナーの長さがどんどん大きくなっていき、テンプレート:Math に至ったところで完全な3周期に変わるテンプレート:Sfn。

テンプレート:Multiple image

このように、ラミナーという秩序的な運動とバーストという乱れた運動が間欠的に繰り返し起こる現象は、間欠性や間欠性カオスと呼ばれるテンプレート:Sfnm。パラメータ テンプレート:Mvar を逆に テンプレート:Math から小さくする方向で考えてみると、これはカオスの発生の一種となっているテンプレート:Sfn。パラメータが窓から離れる方向へ動くほど、バーストが支配的になっていき、最終的には完全なカオス状態となるテンプレート:Sfn。これも前述の周期倍分岐ルートと同じくカオスに至る一般的な道筋の一種で、このような接線分岐による間欠カオスの発生を特徴とした道筋は間欠性ルートと呼ばれるテンプレート:Sfnm。

f ³(x) のグラフで現れるチャネルの様子

間欠性の発生メカニズムもまた、写像のグラフから理解することができるテンプレート:Sfn。テンプレート:Mvar が テンプレート:Math よりもわずかに小さいとき、テンプレート:Math のグラフと対角線の間にはとても小さい隙間が存在するテンプレート:Sfn。この隙間はチャネルと呼ばれ、狭いチャネルを軌道が通過するために多数の写像の反復が起こるテンプレート:Sfn。このチャネルを通り過ぎる過程では テンプレート:Math2 と テンプレート:Math2 はとても近い値になり、実質的にほとんど3周期軌道のように変数が変化するテンプレート:Sfn。これがラミナーに相当するテンプレート:Sfnm。軌道はやがてこの細いチャネルを抜けるが、写像の大域的な構造の結果、ふたたびチャネルに戻って来るテンプレート:Sfnm。チャネルを離れている間はカオス的な乱れた動きをするテンプレート:Sfnm。これがバーストに相当するテンプレート:Sfnm。

バンド、窓の終わり

カオス領域の全体に目を移すと、カオスであっても窓であっても、軌道図の縦軸の最大値と最小値（アトラクタの上限値と下限値）はある範囲内に限られているテンプレート:Sfn。式 (テンプレート:EqNoteN) が示すようにロジスティック写像の最大値は テンプレート:Math で与えられ、これがアトラクタの上限値となるテンプレート:Sfn。アトラクタの下限値は、テンプレート:Math が写る点 テンプレート:Math で与えられるテンプレート:Sfn。結局、軌道図で テンプレート:Mvar が動く最大値と最小値は、パラメータ テンプレート:Mvar に依存して

と与えられるテンプレート:Sfn。最終的には、テンプレート:Math で軌道は テンプレート:Closed-closed 全体に及ぶテンプレート:Sfn。

軌道図を観察すると、点の分布に特徴的な濃淡が見られるテンプレート:Sfn。点が濃い部分は、変数がその周辺の値を取る頻度が大きいことを意味しており、点が薄い部分は、変数がその周辺の値を取る頻度が小さいことを意味しているテンプレート:Sfn。このような点が訪れる頻度の差異は、ロジスティック写像のグラフの形に起因して生まれるテンプレート:Sfn。グラフの最頂部 テンプレート:Math 近辺が高頻度で軌道を呼び込み、そこから写された先の テンプレート:Math 近辺も高頻度になり、そこから写された先の テンプレート:Math 近辺も高頻度になり…、という具合に頻度の分布が生まれるテンプレート:Sfn。写像によって生まれる点の密度分布は不変測度や分布関数と呼ばれる量で特徴づけられ、アトラクタの不変測度は初期値に関わらず再現性があるテンプレート:Sfnm。

軌道図カオス領域の初めの辺り、 テンプレート:Mvar が最初の2周期倍化カスケードの集積点 テンプレート:Math2 を少し超えた辺りを見てみると、軌道がいくつかの区間に分かれていることが観察できるテンプレート:Sfn。このように分かれた小領域はバンドと呼ばれるテンプレート:Sfn。バンドが複数ある場合、軌道は規則的に順番に各バンドを巡り、なおかつ各バンド内での取る値は不規則的となるような振る舞いを示すテンプレート:Sfn。このようなカオス軌道はバンドカオスや周期的カオスと呼ばれ、テンプレート:Mvar 個のバンドから成るカオスは テンプレート:Mvar バンドカオスなどと呼ばれるテンプレート:Sfnm。2バンドカオスであれば、およそ テンプレート:Math2 の範囲内に存在しているテンプレート:Sfn。

バンド構造の様子。e_p の間隔が急激に小さくなっていくため、8バンド以上は図示できていない。軌道が収まっている最上部と最下部の線が式 (テンプレート:EqNoteN) の範囲内にある。

2バンドカオスの左端 テンプレート:Math からさらに値を小さくしていくと、周期倍加分岐のときと同じようにバンドの数が2倍ずつ増えていくテンプレート:Sfn。テンプレート:Math バンドカオスが分裂して テンプレート:Math バンドカオスになる分岐点、あるいは テンプレート:Mvar バンドカオスが融合して テンプレート:Math バンドカオスになる分岐点を テンプレート:Mvar (ただし テンプレート:Math2）で表すとする。すると、周期倍加分岐と同じように テンプレート:Math で テンプレート:Mvar はある値に集積するテンプレート:Sfnm。この集積点 テンプレート:Math2 でバンドの数は無限となり、テンプレート:Math2 の値は テンプレート:Math2 の値と一致するテンプレート:Sfnm。

ロジスティック写像の軌道図全体の自己相似階層構造

テンプレート:Math2 より前に現れた周期倍化分岐カスケードの分岐点についても、同じように、テンプレート:Mvar 安定周期軌道が分岐して テンプレート:Math 安定周期軌道になる分岐点を テンプレート:Mvar（ただし テンプレート:Math2）で表すとする。このとき、テンプレート:Math から テンプレート:Math までの軌道図に着目すると、テンプレート:Math から テンプレート:Math までの全体軌道図の縮小版が テンプレート:Math から テンプレート:Math までの軌道図の中に2つ存在しているテンプレート:Sfn。同様に、テンプレート:Math から テンプレート:Math までの軌道図に着目すると、テンプレート:Math から テンプレート:Math までの全体軌道図の縮小版が テンプレート:Math から テンプレート:Math までの軌道図の中に4つ存在しているテンプレート:Sfn。以下同様に テンプレート:Mvar から テンプレート:Mvar までの軌道図には全体軌道図の縮小版が テンプレート:Mvar 個存在しており、ロジスティック写像の分岐構造は無限の自己相似階層を備えているテンプレート:Sfn。

ロジスティック写像の窓の自己相似階層構造

分岐構造の自己相似階層は、窓の中にも存在するテンプレート:Sfn。窓の中の周期倍化分岐カスケードは、テンプレート:Math 周期分岐のカスケードと同じ筋道をたどるテンプレート:Sfn。つまり、窓の中で無限回の周期倍化分岐が起き、それを過ぎると振る舞いはまたカオスとなるテンプレート:Sfn。例えば周期3の窓では、テンプレート:Math2 で安定な周期軌道のカスケードが終わるテンプレート:Sfn。テンプレート:Math2 を過ぎると、振る舞いは3の倍数のバンドカオスになるテンプレート:Sfn。テンプレート:Mvar が テンプレート:Math2 から増えるにつれて、このバンドカオスも2個ずつ融合していき、窓が終わる最後にはバンドの数は3つになるテンプレート:Sfn。このような窓の中にあるバンドの中にも、無数の窓がまたさらに存在しているテンプレート:Sfnm。結局、窓の中には テンプレート:Math の軌道図全体の縮小版が含まれているような恰好となり、窓の中にも分岐の自己相似階層構造が存在しているテンプレート:Sfnm。

窓が終わると、広範囲のカオスに戻る。周期3の窓であれば、テンプレート:Math2 で最後の3バンドカオスが大きな範囲の1バンドカオスへ変わって窓が終わるテンプレート:Sfnm。しかし、この変化は非連続的で、3バンドのカオスアトラクタは突然大きさを変化させ、1バンドへ変わるテンプレート:Sfn。このようにアトラクタの大きさが非連続的に変わる現象は、クライシスと呼ばれるテンプレート:Sfn。窓の終わりで起きるような種類のクライシスは、特に内部クライシスとも呼ばれるテンプレート:Sfnm。窓の終わりでクライシスが起きるとき、安定な周期軌道が軌道図上では見えない不安定周期点とちょうど接触するテンプレート:Sfn。これによって周期軌道が逃げ出せる出口が生まれ、内部クライシスが発生するテンプレート:Sfn。内部クライシス直後には、ある時間帯では広域のカオスとして振る舞うが、ある時間帯では元のバンドカオス的振る舞いも起こし、窓の始まりと同じような一種の間欠性が現れるテンプレート:Sfn。

a = 4 のとき

パラメータ a = 4 のロジスティック写像のクモの巣図（左）と、n = 500までの時系列図（右）。初期値 x₀ = 0.3 の場合。

パラメータが テンプレート:Math2 に達すると、振る舞いは テンプレート:Closed-closed 全域を経巡るカオスとなるテンプレート:Sfn。このとき、リアプノフ指数 テンプレート:Mvar は最大となり、もっともカオスが強い状態といえるテンプレート:Sfn。テンプレート:Math2 におけるロジスティック写像の テンプレート:Mvar は正確な値を求ることができ、その値は テンプレート:Math2 であるテンプレート:Sfn。カオスの厳密な数学的定義はまだ統一されていないが、よく知られているカオスの定義の一つに対して テンプレート:Math2 のロジスティック写像は テンプレート:Closed-closed 上でカオス的テンプレート:Efnであることが証明できるテンプレート:Sfnm。

a = 4 のときの不変測度 ρ (x) のグラフ。点プロットは、（高さを ρ (x) に合わせた）10000回反復で得られた実際の点の頻度を示す。

点の密度の不変測度 テンプレート:Math も、テンプレート:Math2 のときは次のような正確な関数で与えることができるテンプレート:Sfn。

ここで テンプレート:Math は、写像を反復したときの点 テンプレート:Mvar の全点数に対し、点 テンプレート:Mvar が微小区間 テンプレート:Closed-closed に入る点数の割合が、テンプレート:Math2 で与えられるという意味を持つテンプレート:Sfn。テンプレート:Math2 のロジスティック写像の頻度分布は、テンプレート:Closed-closed の両サイド近辺で密度が高く、テンプレート:Math で最も密度が低い形をしている。

テンプレート:Math のとき、カオス軌道とは別に、あらゆる周期の周期軌道も存在しているテンプレート:Sfn。自然数 テンプレート:Mvar に対して、テンプレート:Math2 のグラフは テンプレート:Math 個の山と テンプレート:Math 個の谷が存在する曲線となり、しかもそれら全ての山と谷は テンプレート:Math と テンプレート:Math に接する状態になるテンプレート:Sfn。したがって、対角線とグラフの交点の数は テンプレート:Math 個あり、テンプレート:Math2 の不動点は テンプレート:Math 個存在するテンプレート:Sfn。この テンプレート:Math 個の不動点には テンプレート:Mvar 周期点も必ず含まれているので、テンプレート:Math2 では任意のテンプレート:Mvar 周期軌道が存在するテンプレート:Sfn。このように、テンプレート:Math のとき テンプレート:Closed-closed 上には周期点が無限に存在しているが、それら周期点は全て不安定であるテンプレート:Sfn。また、区間 テンプレート:Closed-closed という非可算無限の集合に対してそれら周期点の数は可算無限であり、ほとんど全ての初期値から始まる軌道は周期軌道とはならずに非周期軌道となるテンプレート:Sfn。

ロジスティック写像 f_a=4 の軌道を 0 と 1 の記号列に変換すると、あらゆる記号列が再現できる

カオスの重要性の一つに、決定論的性質と確率論的性質の二重性があるテンプレート:Sfn。力学系は決定論的な過程だが、変数が取る範囲を適当に粗視化すると確率的な過程と区別ができなくなるテンプレート:Sfn。テンプレート:Math のロジスティック写像の場合であれば、あらゆるコイン投げの結果をロジスティック写像の軌道で記述できるテンプレート:Sfn。このことを詳述すると次のとおりであるテンプレート:Sfnm。

テンプレート:Math の確率で表裏が出るコイン投げを想定し、何回もコイン投げを続ける。表が出たときを テンプレート:Math、裏が出たときを テンプレート:Math とすれば、表裏表表裏…という結果は テンプレート:Math といったような記号列になる。一方で、ロジスティック写像の軌道 テンプレート:Math2 について、テンプレート:Math 以下のものは テンプレート:Math に テンプレート:Math を超えるものは テンプレート:Math に変換し、軌道を テンプレート:Math と テンプレート:Math から成る記号列に置き換える。例えば、初期値 テンプレート:Math2 とすれば、 テンプレート:Math2 となるので、軌道は テンプレート:Math という記号列になる。前者のコイン投げによる記号列を テンプレート:Mvar とし、後者のロジスティック写像による記号列を テンプレート:Mvar とする。記号列 テンプレート:Mvar には、ランダムなコイン投げで記号を決めていったのであらゆるパターンの数列があり得る。よって、ロジスティック写像による記号列 テンプレート:Mvar がどんなものだったとしても、テンプレート:Mvar の中に同一のものが存在する。そして、「実に驚くべきこと」として、この逆が成立する。つまり、どのような テンプレート:Mvar の記号列であっても、初期値を適切に選びさえすればロジスティック写像の軌道 テンプレート:Mvar によって実現できる。すなわち、任意の テンプレート:Mvar に対し、テンプレート:Math2 となる テンプレート:Math が テンプレート:Closed-closed 中にただ1点存在するテンプレート:Sfnm。

a > 4 のとき

a = 4.5 のロジスティック写像では、[0, 1] のほとんどの全ての点から出発する軌道はマイナス無限大へ向かう

パラメータ テンプレート:Mvar が テンプレート:Math を超えると、ロジスティック写像のグラフの頂点 テンプレート:Math は テンプレート:Math を超えるテンプレート:Sfn。グラフが テンプレート:Math を突き抜けている範囲から、軌道は テンプレート:Closed-closed を抜け出せるようになるテンプレート:Sfn。その結果、テンプレート:Closed-closed のほとんどの全ての点から出発する軌道はどこかの時点で テンプレート:Closed-closed を抜け出し、最終的にマイナス無限大へ発散してしまうテンプレート:Sfn。

この テンプレート:Math で起こる分岐もクライシスの一種で、とくに境界クライシスと呼ばれるテンプレート:Sfn。この場合の境界クライシスでは、テンプレート:Closed-closed にあったアトラクタが不安定化・崩壊し、なおかつ外側にアトラクタも存在しないため、軌道が無限遠へと発散してしまうテンプレート:Sfn。

一方で、テンプレート:Math の条件下でも テンプレート:Closed-closed の中に留まり続ける軌道があるテンプレート:Sfnm。分かりやすい例は テンプレート:Closed-closed 内の不動点や周期点で、これらは テンプレート:Closed-closed の中に留まり続けるテンプレート:Sfnm。しかし、テンプレート:Closed-closed の中に留まり続ける軌道には、不動点や周期点以外の軌道も存在しているテンプレート:Sfn。

テンプレート:Math を満たす テンプレート:Mvar の区間を テンプレート:Math とする。上記の通り、変数 テンプレート:Mvar が テンプレート:Math に一旦入ると、マイナス無限大へ発散する。写像を1回適用すると テンプレート:Math へ写る テンプレート:Mvar も テンプレート:Closed-closed の中に存在している。この テンプレート:Mvar の区間は2つに分かれており、それらをまとめて テンプレート:Math とする。同じように、写像を1回適用すると テンプレート:Math へ写る区間も4つ存在し、それらを テンプレート:Math とする。以下同じように、テンプレート:Mvar 回反復で テンプレート:Math にたどり着く区間 テンプレート:Mvar が テンプレート:Math 個存在するテンプレート:Sfn。 したがって、次のように テンプレート:Closed-closed から テンプレート:Mvar を無限回取り除いた区間 テンプレート:Mvar が、テンプレート:Mvar の中に留まり続ける軌道の集まりであるテンプレート:Sfn。

テンプレート:Closed-closed から テンプレート:Mvar を取り除いていく作業は上述のカントール集合の構成過程に似ており、実際に テンプレート:Mvar はカントール集合（閉で完全不連結でテンプレート:Closed-closed の完全部分集合）の形で テンプレート:Closed-closed の中に存在しているテンプレート:Sfnm。そしてさらに、テンプレート:Mvar 上でロジスティック写像 テンプレート:Math はカオス的であるテンプレート:Sfn。

a < 0 のとき

ロジスティック写像は生態学上のモデルとして研究された経緯もあり、パラメータ テンプレート:Mvar が負の場合について論じられることは少ない。テンプレート:Mvar を テンプレート:Math から減少させていくと、テンプレート:Math2 では テンプレート:Math2 の安定不動点に漸近するが、テンプレート:Math2 を超えたところから2周期点に分岐し、正のときと同じく周期倍化分岐を経てカオスへ至る。最終的には、テンプレート:Math2 を下回るとプラス無限大へ発散するようになる。

パラメータ a が −2 から 4 までの軌道図。負側も正側もこれらのパラメータ範囲を超えると発散する。

特別な場合の厳密解

パラメータ テンプレート:Mvar が特定のロジスティック写像については、時刻 テンプレート:Mvar と初期値 テンプレート:Math を陽に含む厳密解が以下のように得られている。

テンプレート:Math のとき

テンプレート:Math のとき

テンプレート:Math のとき

以上3つの厳密解を考察すると、いずれの解も テンプレート:NumBlk という形になっている。ここで、テンプレート:Mvar は何かしらの適当な関数、テンプレート:Math はその逆関数を意味する。テンプレート:Math では テンプレート:Math、テンプレート:Math では テンプレート:Math、テンプレート:Math では テンプレート:Math である。ただし、任意の テンプレート:Mvar について一般的にロジスティック写像の厳密解を表すことができるような、数学的に標準的な関数の テンプレート:Mvar は存在しない。

普遍性

同種の振る舞いを示す写像のクラス

正弦写像 (テンプレート:EqNoteN) のグラフ

正弦写像 (テンプレート:EqNoteN) の軌道図

ロジスティック写像で現れた上記の分岐のパターンは、ロジスティック写像に限定されないテンプレート:Sfn。ある条件を満たした写像で、この分岐パターンが共通して現れるテンプレート:Sfn。次の正弦関数を使った力学系はその一例であるテンプレート:Sfn。

ここで、定義域は テンプレート:Math2 かつ テンプレート:Math2 とするテンプレート:Sfn。この正弦写像 (テンプレート:EqNoteN) は、ロジスティック写像 (テンプレート:EqNoteN) と定性的に同一の振る舞いを起こすテンプレート:Sfn。つまり、この写像でも、ロジスティック写像と同じようにパラメータ テンプレート:Mvar の増加にともなって周期倍化ルートを経てカオスになり、さらにはカオス領域には窓が同じように存在しているテンプレート:Sfn。

ロジスティック写像も正弦写像も区間 テンプレート:Closed-closed を テンプレート:Closed-closed へ写す1次元写像で、単峰と呼ばれる次の性質を満たしているテンプレート:Sfn。

1. テンプレート:Math2 を満たす。
2. 写像は可微分で、テンプレート:Closed-closed 中に テンプレート:Math を満たす臨界点 テンプレート:Mvar が唯一存在する。

一般的に、1パラメータ・1変数のある1次元写像が単峰で、頂点近辺を2次の多項式で近似できるような曲線であれば、具体的な写像の形に依存せずに、パラメータ範囲 テンプレート:Math2 で見たような無限の周期倍化カスケードの分岐が起き、 さらに式 (テンプレート:EqNoteN) で定義される比率 テンプレート:Mvar はファイゲンバウム定数 テンプレート:Math2 に一致するテンプレート:Sfnm。

また、ロジスティック写像で現れた安定周期軌道の出現パターンにも普遍性があるテンプレート:Sfn。パラメータを テンプレート:Mvar として、テンプレート:Math2 で表される単峰な写像では、2つの不動点が不安定であるようなあるパラメータ区間で様々な周期の安定周期軌道が出現し続け、その出現パターン（ある周期の安定周期軌道の出現回数と出現順序）は共通であることが知られているテンプレート:Sfn。つまり、この種の写像であれば、写像の具体的な形によらずに安定周期軌道の系列は同じとなるテンプレート:Sfn。ロジスティック写像の場合は テンプレート:Math がそのパラメータ区間であったが、正弦写像 (テンプレート:EqNoteN) では テンプレート:Math が共通する安定周期軌道の系列が起きるパラメータ区間である。この普遍性のある安定周期軌道の系列はU系列と呼ばれるテンプレート:Sfn。

加えて、ロジスティック写像は区間 テンプレート:Closed-closed 上でシュワルツ微分が常に負であるという性質を持つ。ある （テンプレート:Math 級の）写像 テンプレート:Mvar のシュワルツ微分とは、

で定義される関数であるテンプレート:Sfn。実際にロジスティック写像のシュワルツ微分を計算すると

となり、テンプレート:Mvar および テンプレート:Mvar の値に依らずにシュワルツ微分は負となるテンプレート:Sfn。テンプレート:Closed-closed を テンプレート:Closed-closed へ写す1次元写像が単峰で負のシュワルツ微分を持てば、存在する安定周期軌道は多くても1つであるといった性質が知られるテンプレート:Sfn。

位相共役な写像

記号 テンプレート:Math で写像の合成を表すとする。一般的に、位相空間 テンプレート:Math2 について、2つの写像 テンプレート:Math と テンプレート:Math が同相写像 テンプレート:Math によって

という関係を持つとき、テンプレート:Mvar と テンプレート:Mvar は位相共役であるというテンプレート:Sfn。位相共役という概念は、力学系の研究上で重要な役割を果たすテンプレート:Sfn。位相共役な テンプレート:Mvar と テンプレート:Mvar は本質的に同一な振る舞いを示し、テンプレート:Mvar の振る舞いが周期的であれば テンプレート:Mvar も周期的であり、テンプレート:Mvar の振る舞いがカオス的であれば テンプレート:Mvar もカオス的であるテンプレート:Sfn。

特に同相写像 テンプレート:Mvar が線形であれば、テンプレート:Mvar と テンプレート:Mvar は線形共役であるというテンプレート:Sfn。全ての2次関数は他の全ての2次関数と線形共役にあるテンプレート:Sfn。したがって、 テンプレート:NumBlk テンプレート:NumBlk テンプレート:NumBlk などは、任意のパラメータ テンプレート:Mvar のロジスティック写像と線形共役であるテンプレート:Sfnm。式 (テンプレート:EqNoteN) や式 (テンプレート:EqNoteN) の形のものもロジスティック写像と呼ばれたりもするテンプレート:Sfnm。特に式 (テンプレート:EqNoteN) の形だと計算量が減るため、長時間を要する数値計算に向いているテンプレート:Sfn。

テント写像 (テンプレート:EqNoteN) の軌道の様子。a = 4 のロジスティック写像と位相共役な関係を持つ。

また、テンプレート:Math のロジスティック写像 テンプレート:Math は、次のテント写像 テンプレート:Math やベルヌーイシフト写像 テンプレート:Math と位相共役な関係にあるテンプレート:Sfn。

ロジスティック写像 テンプレート:Math が厳密にカオス的であることの証明や、テンプレート:Math の厳密解 (テンプレート:EqNoteN) の導出に、これらの位相共役の関係を利用できるテンプレート:Sfnm。

あるいは、記号力学系の考え方を導入して、上記で導入したような テンプレート:Math と テンプレート:Math の列から成る記号列空間上に定義される次のようなシフト写像 テンプレート:Mvar を考えるとするテンプレート:Sfn。

ここで、テンプレート:Mvar は テンプレート:Math または テンプレート:Math である。式 (テンプレート:EqNoteN) で導入した集合 テンプレート:Mvar 上で、ロジスティック写像 テンプレート:Math はシフト写像と位相共役であるので、これを利用して テンプレート:Mvar 上の テンプレート:Math がカオス的であることを導けるテンプレート:Sfn。

生物個体数モデルとしてのロジスティック写像

離散型個体群モデル

ロジスティック写像は、イギリスの数理生物学者ロバート・メイの研究を発端にして、生物の個体数の変化を考える式として世に広まったテンプレート:Sfnm。このような生物個体数としてのロジスティック写像では変数 テンプレート:Mvar は、ある環境中に生息する生き物の個体数（より専門的には個体群サイズ）を意味するテンプレート:Sfn。さらに、個体がその環境から出たり、外部の個体が環境に入ってきたりしない場合（あるいは移出入があっても実質的な影響がない場合）を想定しており、このような状況での個体数の増減を考える数理モデルが数理生物学上のロジスティック写像であるテンプレート:Sfn。

生物の個体数の増殖を考える数理モデルには、差分方程式を使った離散的な時間のモデルと微分方程式を使った連続的な時間のモデルの2種類があるテンプレート:Sfn。例えば、卵を産むとすぐに死ぬような種類の昆虫では、その昆虫の個体数は、1世代目の個体数、2世代目個体数…というように各世代ごとに数えられるテンプレート:Sfn。このような例は、前者の離散時間モデルに適合するテンプレート:Sfn。一方で、各世代が連続的に重なり合っているような場合は、連続時間モデルと親和性があるテンプレート:Sfn。ロジスティック写像は、このような離散型あるいは世代分離型の個体群モデルに相当するテンプレート:Sfnm。

ある環境中の単一種の生物の個体数を テンプレート:Mvar で表すとする。もっとも単純な個体数の増殖の仕方として、個体数に対して常に一定の割合で増え続けるモデルが考えられる。そのような個体数増加モデルはマルサスモデルと呼ばれ、次のような形で表されるテンプレート:Sfn。

ここで、テンプレート:Mvar は テンプレート:Mvar 世代目の個体数を意味しており、テンプレート:Mvar は個体数の増殖率で正の定数であるテンプレート:Sfn。しかし、モデル (テンプレート:EqNoteN) では個体数が無尽蔵に増え続け、ほとんどの実現象に対して非現実的なモデルといえるテンプレート:Sfnm。ある環境が養える個体数には限度があるので、個体数 テンプレート:Mvar が増えていくと増殖率 テンプレート:Mvar は低下していくのが自然に思われるテンプレート:Sfn。このように個体数密度の変化によって増殖率が変化することを密度効果と呼ぶテンプレート:Sfn。密度効果をモデル (テンプレート:EqNoteN) に反映した改良モデルとして、もっとも単純なものとして次のような差分方程式が考えられるテンプレート:Sfn。

ここで、テンプレート:Mvar はその環境中で可能な最大増殖率を意味し、テンプレート:Mvar は密度効果の影響の強さを意味しているテンプレート:Sfn。モデル (テンプレート:EqNoteN) は、増殖率が個体数に単純に比例して下がっていくと想定しているテンプレート:Sfn。式 (テンプレート:EqNoteN) の テンプレート:Mvar を

と変数変換すると、以下のロジスティック写像が導出されるテンプレート:Sfn。

生物の個体数として式 (テンプレート:EqNoteN) あるいは式 (テンプレート:EqNoteN) を扱う際には、テンプレート:Mvar あるいは テンプレート:Mvar が負になると個体数としての意味を為さなくなるテンプレート:Sfn。そうならないために、初期値 テンプレート:Math に対して テンプレート:Math2 という条件が、パラメータ テンプレート:Mvar に対して テンプレート:Math2 という条件が要求されるテンプレート:Sfn。

他には、想定している環境が養える最大の個体数 テンプレート:Mvar を仮定し、これを使って

という形で密度効果を取り込んだ差分方程式を考え、テンプレート:Math2 と変数変換してロジスティック写像を導くこともあるテンプレート:Sfn。この場合、変数 テンプレート:Mvar は、最大個体数 テンプレート:Mvar に対する個体数 テンプレート:Mvar の比率を意味しているテンプレート:Sfn。

ロジスティック方程式の離散化

ロジスティック写像は、連続時間型の個体群モデルのロジスティック方程式の離散化からも導出できるテンプレート:Sfn。ロジスティック写像の名も、ロバート・メイがロジスティック方程式の離散化からロジスティック写像を導入したことに由来するテンプレート:Sfn。ロジスティック方程式とは、次のような生物個体数の時間変化を表す常微分方程式であるテンプレート:Sfn。

ここで、テンプレート:Mvar は生物個体数や個体数密度、テンプレート:Mvar は連続的な時間、テンプレート:Mvar と テンプレート:Mvar がパラメータである。テンプレート:Mvar は環境収容力、 テンプレート:Mvar は内的自然増加率とも呼ばれ、通常は正の値を取るテンプレート:Sfn。この式の左辺 テンプレート:Math は時刻 テンプレート:Mvar における個体群サイズの変化速度を意味しているテンプレート:Sfn。

ロジスティック方程式の解の例。個体数 N は時間 t が経過すると初期値によらず環境収容力 K に収束する。

ロジスティック方程式 (テンプレート:EqNoteN) は、ロジスティック写像 (テンプレート:EqNoteN) と一見似ているが、解の振る舞いはロジスティック写像とは大きく異なるテンプレート:Sfn。初期値 テンプレート:Math が正である限り、ロジスティック方程式の個体数 テンプレート:Mvar は常に単調に テンプレート:Mvar に収束するのみであるテンプレート:Sfn。

このロジスティック方程式に、1階常微分方程式の数値解法の一つであるオイラー法による差分化近似を施すことによって、ロジスティック写像が導出できるテンプレート:Efn。オイラー法の差分化近似とは、適当な時間間隔（時間刻み幅）テンプレート:Mvar を導入し、増殖率 テンプレート:Math を以下のように近似することであるテンプレート:Sfnm。

この近似の結果、次のロジスティック写像が導かれるテンプレート:Sfnm。

ただし、この式の テンプレート:Mvar と テンプレート:Mvar は、元のパラメータ、変数、時間刻み幅と次のような関係を持つテンプレート:Sfnm。

テンプレート:Mvar が十分小さければ、式 (テンプレート:EqNoteN) は元の式 (テンプレート:EqNoteN) の有効な近似として働き、テンプレート:Math2では元の式の解と一致するテンプレート:Sfn。一方で、テンプレート:Mvar が大きいと、元の式の解から外れていくテンプレート:Sfn。また、式 (テンプレート:EqNoteN) の関係から、テンプレート:Mvar を大きくすることはパラメータ テンプレート:Mvar を大きくすることに相当するテンプレート:Sfn。よって、テンプレート:Mvar を大きくするほど、元の方程式との誤差を単に大きくするだけでなく解にカオス的振る舞いを生み出すことになるテンプレート:Sfn。

位置付け

以上のように、生物の個体群動態論上では、ロジスティック写像は離散型増殖過程のモデルの一つである。ただし、生物の個体数のモデルとしてのロジスティック写像は、物理学の法則などとは異なり、直接的な実験結果や普遍的に成立する原理から導かれたものではないテンプレート:Sfn。導出過程の考え方にある程度の合理性はあるが、基本的には頭の中で考えられた「モデル」に留まるテンプレート:Sfn。ロジスティック写像を著名にしたメイも、論じているモデルが個体数の増減を正確に表現していると主張していたわけではない。生物個体群ダイナミクスの研究上も、歴史的に多用されてきたのは微分方程式による連続時間モデルであり、それら連続時間モデルの適用によって生物個体群ダイナミクスの理解を深めてきたテンプレート:Sfn。密度効果を考慮した離散時間個体群モデルとしても、個体数が負にならないリッカーモデルの方がより現実的と言えるテンプレート:Sfn。

一般的に言えることとして、数理モデルは個体群ダイナミクスに関する重要な定性的情報を提供してくれることもあるが、実験的な裏付けがないのであれば、数理モデルから出てくる結果をあまり真剣に受け止めるべきではないテンプレート:Sfn。数理モデルの結論が生物学的研究結果から外れることがあっても、なおも数理モデルによる研究が有意義なのは、有用な対照となりうるからであるテンプレート:Sfn。モデルの構成過程や設定、あるいはモデルが前提としていた生物学的な知見や仮説を見直すことにより、生物学的論点を提示できる可能性があるテンプレート:Sfn。生物個体数モデルとしてのロジスティック写像は単純過ぎて現実的ではないが、ロジスティック写像が示す結果は、環境からの不規則的な影響などに無関係に、個体群それ自体に内在するダイナミクスによって個体数の多様な変動が起こる可能性を示唆している。

応用

結合写像系

1変数のロジスティック写像は、系としての自由度あるいは次元は テンプレート:Math であるテンプレート:Sfnm。一方で実際の自然界では、時間的に乱れるだけでなく、多数の空間自由度を持ち空間的にも乱れるような多自由度のカオスが多いと考えられるテンプレート:Sfn。あるいは、カオス的運動を行う振動子の同期現象も研究対象であるテンプレート:Sfn。こういったものを調べるために、差分方程式（写像）を多数結合させる結合写像の手法があるテンプレート:Sfn。結合写像モデル研究の題材として、ロジスティック写像がしばしば採用されるテンプレート:Sfnm。その理由には、ロジスティック写像自体はすでにカオスの典型的モデルとしてよく調べられており、その蓄積があることが挙げられるテンプレート:Sfn。

結合写像モデルでの具体的な結合のさせ方には、様々な手法が存在するテンプレート:Sfn。全部で テンプレート:Mvar 個の写像が結合し、テンプレート:Mvar 番目の写像の時刻 テンプレート:Mvar における状態が テンプレート:Math で表されるとする。大域結合写像と呼ばれる手法では、テンプレート:Math を次のように定式化するテンプレート:Sfnm。

結合振動子の研究の流れでは、次のように変数の差分で振動子2つ テンプレート:Mvar と テンプレート:Mvar を結合させた最も簡単な次のモデルなどが挙げられるテンプレート:Sfn。

これらの式中の テンプレート:Math が、結合写像モデルに組み込む具体的な写像であり、ロジスティック写像が用いられる場合はここに適用されるテンプレート:Sfnm。

a = 3.8 と D = 0.43 の結合写像モデル (テンプレート:EqNoteN) の2つの変数の変化（上）とそれらの差（下）。2つの変数は、同期の後に不意に非同期状態になり、また同期状態に戻る。

式 (テンプレート:EqNoteN) および (テンプレート:EqNoteN) 中の テンプレート:Mvar や テンプレート:Mvar は結合係数などと呼ばれる、写像同士の結合の強さを意味するパラメータであるテンプレート:Sfnm。他方で、ロジスティック写像を結合写像モデルに組み込む場合、ロジスティック写像のパラメータ テンプレート:Mvar はモデルの非線形性の強さを意味するテンプレート:Sfn。テンプレート:Mvar の値と テンプレート:Mvar または テンプレート:Mvar の値を変化させることで、ロジスティック写像の結合写像系では様々な現象が現れる。例えばモデル (テンプレート:EqNoteN) では、テンプレート:Mvar をある値 テンプレート:Math 以上に大きくすると、テンプレート:Mvar と テンプレート:Mvar は同期しながらカオス振動を行うテンプレート:Sfn。テンプレート:Math 未満でも常にバラバラのカオス振動が起こるだけでないテンプレート:Sfn。テンプレート:Mvar がある範囲のときは、テンプレート:Math2 であるにもかかわらず テンプレート:Mvar と テンプレート:Mvar は2周期振動を起こすテンプレート:Sfn。テンプレート:Math2 では、同期状態と非同期状態が交互に起こり続けるような振る舞いも見られるテンプレート:Sfn。

大自由度の大域結合写像 (テンプレート:EqNoteN) にロジスティック写像を適用した研究では、カオス的遍歴と呼ばれる現象も見つかっているテンプレート:Sfnm。これはいくつかのクラスターでまとまって振動する秩序的な状態から乱れた状態になり、また別のクラスター状態になり、再度乱れた状態になり…、という振る舞いを繰り返す現象で、相空間上でアトラクタの残骸と言われるような領域を軌道が経巡ることで起こると考えられているテンプレート:Sfnm。

擬似乱数生成器

コンピューターシミュレーションや情報セキュリティ分野では、計算機で擬似乱数を作成することが重要な技術の一つで、擬似乱数を作る手法の一つとしてカオスの活用が考えられる。カオスからの擬似乱数生成器で十分な性能を持つものはまだ実現されていないが、これまでにいくつかの手法が提案されてきた。ロジスティック写像についても、これまでにカオスに基づく擬似乱数生成器の可能性が複数の研究者たちによって調べられてきている。

ロジスティック写像の擬似乱数生成には、パラメータ テンプレート:Math2 がよく利用されている。歴史的にも、後述の通り、電子計算機の誕生から間もない1947年にスタニスワフ・ウラムとジョン・フォン・ノイマンも テンプレート:Math2 のロジスティック写像を使った擬似乱数生成器の可能性を指摘している。しかし、ロジスティック写像 テンプレート:Math の点の分布は、式 (テンプレート:EqNoteN) で示されるような分布になっており、出てくる数値が テンプレート:Math と テンプレート:Math の近くに偏る。そのため、偏りのない一様乱数を得るためには何らかの処理が必要となる。その方法としては、

1. 得られた数値をテント写像 (テンプレート:EqNoteN) との関係を用いて一様分布に変換する方法
2. 得られた数値を上述のコイン投げの比喩のように閾値を使って テンプレート:Math か テンプレート:Math に変換し、これを繰り返して一様乱数のビット列を得る方法

などがある。また、ロジスティック写像で得られる数列の テンプレート:Math とテンプレート:Math には強い相関があり、擬似乱数の数列としては問題となる。これを解消する方法の一つは、写像1回適用ごとの数列 テンプレート:Math2 を作るのではなく、適当な テンプレート:Math 回反復ごとに数列 テンプレート:Math2 を作る必要がある。例えば、1番の方法に対しては テンプレート:Math または テンプレート:Math で、2番の方法に対しては テンプレート:Math で良好な擬似乱数が得られるといわれる。

コンピュータを用いてデジタルにカオスを計算する一般的問題として、コンピュータでは有限計算精度で計算するため、カオス本来の真に非周期な数列を原理的に得ることができず代わりに有限の周期列が出力されるという問題点がある。原理的に非周期列が得られない場合であっても、擬似乱数生成のためにはできるだけ長い周期の数列が望ましい。しかし、単精度浮動小数点数計算でロジスティック写像 テンプレート:Math が実際に出力する数列の周期性を調べた結果によると、割り当てられたビット数から可能な最大周期に比べて実際に出力される数列の周期はとても小さくなることが報告されており、この観点からメルセンヌ・ツイスタのような既存の擬似乱数生成器に比べてロジスティック写像による擬似乱数生成は劣ると指摘されている。また、ロジスティック写像 テンプレート:Math では、計算途中で数値が不動点 テンプレート:Math に落ち入り、そのまま一定値になるおそれもある。一方で、ロジスティック写像では、開区間 テンプレート:Open-open の中で常に値を取るので、浮動小数点だけでなく固定小数点でも問題無く計算でき、固定小数点計算の利点を享受できる。固定小数点であれば、同じビット数で比較して浮動小数点よりも長い周期の数列になることや意図しない テンプレート:Math への収束が無くせることが指摘されている。

複素数への拡張

ロジスティック写像の軌道図（上）とマンデルブロー集合（下）の対応関係

複素解析関数で定義された力学系も興味を持たれる対象であるテンプレート:Sfn。その例が、次の2次関数で定義される力学系であるテンプレート:Sfnm。

ただし、ここでのパラメータ テンプレート:Mvar と変数 テンプレート:Mvar は複素数であるテンプレート:Sfnm。この写像は、ロジスティック写像 (テンプレート:EqNoteN) と基本的には同じものと言えるテンプレート:Sfn。上記でも述べたとおり、写像 (テンプレート:EqNoteN) は、線形関数によってロジスティック写像 (テンプレート:EqNoteN) と位相共役な関係にあるテンプレート:Sfnm。

パラメータ テンプレート:Mvar を固定し、初期値 テンプレート:Math を変えながら写像 (テンプレート:EqNoteN) の反復の行く末を計算したとき、テンプレート:Math2 でも テンプレート:Mvar が無限大へ発散しないような テンプレート:Math の集まりを充填ジュリア集合というテンプレート:Sfn。さらに、充填ジュリア集合の境界をジュリア集合というテンプレート:Sfn。また、初期値を テンプレート:Math2 に固定し、パラメータ テンプレート:Mvar を変えながら写像 (テンプレート:EqNoteN) の反復を計算したとき、 テンプレート:Mvar が無限大へ発散しないような テンプレート:Mvar の集まりをマンデルブロー集合というテンプレート:Sfn。写像 (テンプレート:EqNoteN) のジュリア集合やマンデルブロー集合から、「神秘的に見える」「怪奇を極めている」などと形容されるフラクタル図形が生成されるテンプレート:Sfnm。

特にマンデルブロー集合では、図形の各円板はある周期の漸近安定な周期軌道の領域に相当するテンプレート:Sfn。ロジスティック写像の軌道図とマンデルブロー集合の図形を並べると、ロジスティック写像軌道図の漸近安定な不動点、周期倍化分岐、周期3の窓などがマンデルブロー集合図形と実軸上で対応していることが分かるテンプレート:Sfnm。

時間遅れを持つ場合

遅延ロジスティック写像の軌道の様子。左右の図で初期値 (x₀, y₀) は同じだが、a = 2 での分岐を境に軌道が引き付けられる先が閉曲線（左）と点（右）に分かれる。

ロジスティック写像を生物の各世代の個体数を表すモデルと解釈すると、次の世代の個体数が現在の世代の個体数だけでなく、その1つ前の世代の個体数も現在の世代に影響する場合も考えられるテンプレート:Sfn。そのような例が

という差分方程式で、1つ前の世代の個体数 テンプレート:Math がマイナスの密度効果として式に取り込まれているテンプレート:Sfn。テンプレート:Math2 とおけば、式 (テンプレート:EqNoteN) は次のような2変数差分方程式に置き換えられるテンプレート:Sfn。

この力学系は準周期アトラクタの分岐の研究などに用いられ、遅延ロジスティック写像やディレイドロジスティックマップ（テンプレート:Lang-en）と呼ばれるテンプレート:Sfn。遅延ロジスティック写像では テンプレート:Math2 でネイマルク・サッカー分岐が起き、漸近安定な不動点が不安定になり、その不安定な不動点の周りに漸近安定な不変曲線ができるテンプレート:Sfn。

研究史

カオス命名以前

写像の反復が力学系と関連する意味を持つ以前の時代、数学者のガストン・ジュリアとピエール・ファトゥが複素関数の反復について研究していた。ジュリアとファトゥの研究は解析関数を中心とした広範なものだったがテンプレート:Sfn、とくに式 (テンプレート:EqNoteN) でも示した以下の複素2次関数の振る舞いが1920年代に彼らによって研究されたテンプレート:Sfn。

ジュリアとファトゥもジュリア集合の中にカオス的振る舞いを理解していたが、当時はコンピュータ・グラフィックスなども無かったこともあって、彼らに続く人物が現れず研究は止まってしまったテンプレート:Sfn。その後1970年代後半まで複素力学系の研究は下火が続き、複素平面上の写像が示す豊かな力学系的振る舞いが着目されるのはベノワ・マンデルブロなどの登場を待つことになるテンプレート:Sfn。

スタニスワフ・ウラム

ジョン・フォン・ノイマン

1947年、数学者のスタニスワフ・ウラムとジョン・フォン・ノイマンは “On combination of stochastic and deterministic processes”（参考訳：確率論的過程と決定論的過程の結合に関して）と題した短いレポートで、

という2次関数の反復合成によって疑似乱数を生成できることを指摘しているテンプレート:Sfn。この式は、現在的な視点では テンプレート:Math のロジスティック写像に相当するテンプレート:Sfn。この当時、「カオス」という言葉もまだ使われていないが、ウラムとフォン・ノイマンは非線形関数による複雑な数列の生成にすでに注目していたといえる。また、ウラムとフォン・ノイマンのレポートでは、写像 (テンプレート:EqNoteN) とテント写像が位相共役の関係にあることや、この写像の数列の不変測度が式 (テンプレート:EqNoteN) で与えられることも明らかにしたテンプレート:Sfn。

その後、任意のパラメータ テンプレート:Mvar を備えた形式の2次写像についても、詳細な調査がいくつかあった。1958年から1963年にかけて、フィンランドの数学者テンプレート:仮リンク は、テンプレート:Mvar をパラメータとする

という形式の2次写像の分岐現象を調べた。この一連の研究は力学系として本質的なもので、ミュルバークは、この写像の周期倍加分岐カスケードを調査して集積点 テンプレート:Math2 の存在も示している。他には、1964年のソビエトのテンプレート:仮リンク、1969年のフランスのイーゴリ・グモウスキーとクリスチャン・ミラ 、1973年のテンプレート:仮リンクらの仕事などが、ロジスティック写像のような単純な1変数差分方程式の異常な振る舞いを明らかにしているテンプレート:Sfn。

ロバート・メイの研究

ロバート・メイ（2009年撮）

その後1970年初頭に、数理生物学者のロバート・メイが、生態学の問題に取り組む過程で式 (テンプレート:EqNoteN) のモデルに出会うテンプレート:Sfn。メイはロジスティック方程式の離散時間化から式 (テンプレート:EqNoteN) すなわちロジスティック写像を導入したテンプレート:Sfn。ロジスティック写像の振る舞いを数理的に解析し、メイは1973年や1974年にその成果を発表したテンプレート:Sfn。ロジスティック写像の数値実験が行われ、パラメータ テンプレート:Mvar による振る舞いの変化が調べられたテンプレート:Sfn。1976年には、”Simple mathematical models with very complicated dynamics”（参考訳：極めて複雑な振る舞いを有する単純な数理モデル）と題した論文を Nature から発表したテンプレート:Sfn。

1976年の論文はレビュー論文で、ロジスティック写像を題材にしながら、単純な非線形関数でも周期倍化分岐カスケードやカオスのような非常に複雑な振る舞いが起こることについて強調し、注意を促す内容であったテンプレート:Sfnm。特にこの論文は、メイの数理生物学者としての地位、研究結果の明快さ、そして何よりも単純な放物線の式が驚くべき複雑な振る舞いを生み出すという衝撃的な内容によって、大きな反響を巻き起こして科学界へと受け入れられたテンプレート:Sfn。このようなメイの研究を経て、ロジスティック写像は多くの研究者をカオス研究へ惹きつけ、カオス研究の流れを改めて再スタートさせたと評されるほど著名な数理モデルとなったテンプレート:Sfnm。

メイの研究以後

メイは、テンプレート:仮リンクとテンプレート:仮リンクが論文 ”Period three implies chaos”（参考訳：3周期はカオスを意味する）で使った「カオス」という表現を積極的に用い、この論文にも注目を集めた。異論もあるが、このリーとヨークの論文は「カオス」という語を数学用語として最初に使ったと考えられており、同論文によって決定論的な無秩序的振る舞いを指す用語「カオス」が生まれたとされるテンプレート:Sfnm。リーとヨークは、1973年に同論文を一旦完成させたが、テンプレート:仮リンク に投稿したところ研究色が強過ぎるので分かりやすく大幅に書き直すように告げられ、掲載を却下されたテンプレート:Sfn。その後、論文は書き直されることなく放っておかれていた。しかし、翌1974年にリーとヨークが居たメリーランド大学にメイが特別招待講義にやってきて、ロジスティック写像の話をした。当時、メイは、ロジスティック写像のカオス領域で何が起きているのかまだ理解できていなかったが、リーとヨークもまた、ロジスティック写像の周期倍化カスケードについて知らなかったテンプレート:Sfn。メイの話に興奮したリーとヨークは、講義後にメイを捕まえて2人が得た結果の話をし、メイもその結果に驚いたテンプレート:Sfn。すぐにリーとヨークは却下された論文を書き直して、再提出された論文は1975年に出版されたテンプレート:Sfn。

ミッチェル・ファイゲンバウム（2006年撮）

また1975年頃、数理物理学者のミッチェル・ファイゲンバウムは、ロジスティック写像の周期倍化カスケードに注目すると、分岐値が等比級数的に収束するスケーリングの法則に気づき、今ではファイゲンバウム定数と呼ばれる定数の存在を数値実験から発見したテンプレート:Sfn。メイもテンプレート:仮リンクとともにそのスケーリング則に気づいていたが、深く追うことまではできなかったテンプレート:Sfn。ファイゲンバウムは、式 (テンプレート:EqNoteN) で示した正弦写像でも同じ定数が現れることを発見し、このスケーリング則にはロジスティック写像だけに留まらない普遍性があることを知ったテンプレート:Sfn。1980年には、この結果に対する厳密な証明がテンプレート:仮リンク、テンプレート:仮リンク、テンプレート:仮リンクらによって与えられたテンプレート:Sfnm。ファイゲンバウムとほぼ同時期あるいはその後、物理学者たちによって実現象に同じ周期倍化カスケードとファイゲンバウム定数が発見され、あくまでも数学的現象と見られていたカオスは物理学方面にも大きな衝撃を与えることとなるテンプレート:Sfnm。

ただし、カオス流行以前の研究成果が軽視され、それらの研究成果の多くまでもがロジスティック写像などを用いた再発見者の功績扱いされる風潮への批判もある。メイ自身も先行研究があったことを尊重した上で、自身の功績は「2次写像の奇怪な数学的挙動を独立に最初に発見」したのではなく、自分は「科学におけるその広範な意味づけを最後に強調した研究者たち」の一人であると位置付けているテンプレート:Sfn。数学者のテンプレート:仮リンクは、自著でロジスティック写像の解説に入る前に次のように語っているテンプレート:Sfn。 テンプレート:Bquote

参照文献

※文献内の複数個所に亘って参照したものを特に示す。

• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp

• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite book ja-jp
• テンプレート:Cite journal

外部リンク

• テンプレート:MathWorld
  • テンプレート:MathWorld
  • テンプレート:MathWorld
  • テンプレート:MathWorld
• テンプレート:JGLOBAL ID