外積代数

外積代数（がいせきだいすう、テンプレート:Lang-de-short、テンプレート:Lang-en-short）は、ヘルマン・グラスマンによって導入された代数。グラスマンに因みグラスマン代数（テンプレート:Lang-de-short、テンプレート:Lang-en-short）とも呼ばれる。

以下、特に断らない限り外国語表記はドイツ語、英語の順に記す。

概要

ベクトルの外積（がいせき、テンプレート:De, テンプレート:En）や楔積（くさびせき、テンプレート:Lang-en-short）は、クロス積をある特定の性質に着目して、より高次元の場合へ一般化する代数的な構成である。

クロス積やスカラー三重積のようにベクトル同士の外積はユークリッド幾何学において面積や体積およびそれらの高次元における類似物の研究に用いられる。線型代数学において外積は、線型変換の行列式や小行列式を記述する基底の取り方に依存しない抽象代数的な仕方を提供し、階数や線型独立性といった概念に根本的に関係してくる。

外積代数（グラスマン代数）は、与えられた体 テンプレート:Mvar 上のベクトル空間 テンプレート:Mvar 上の外積によって生成される多元環である。多重線型代数やその関連分野と同様に、微分形式の成す多元環を通じて現代幾何学、特に微分幾何学と代数幾何学において広く用いられる。

形式的には、外積代数は テンプレート:Math あるいは テンプレート:Math で表され、テンプレート:Mvar を線型部分空間として含む、外積あるいは楔積と呼ばれる テンプレート:Math で表される乗法を持つ、体 テンプレート:Mvar 上の単位的結合代数である。外積は結合的で双線型な乗法

$\wedge :\bigwedge (V)\times \bigwedge (V)\to \bigwedge (V);(\alpha ,\beta )\mapsto \alpha \wedge \beta$

であり、テンプレート:Mvar 上の交代性

(1) 任意の $v\in V$ に対して $v\wedge v=0$

を持つものである。これは以下の性質

(2) 任意の $u,v\in V$ に対して $u\wedge v=-v\wedge u$

(3) $v_1,\dots ,v_k\in V$ が一次従属ならば $v_1\wedge v_2\wedge \cdots \wedge v_k=0$

を特別の場合として含む。

圏論の言葉で言えば、外積代数は普遍構成によって与えられる、ベクトル空間の圏上の函手の典型である。この普遍構成によって、体上のベクトル空間だけに限らず、可換環上の加群やもっとほかの興味ある構造にたいしても外積代数を定義することができる。外積代数は双代数のひとつの例である。つまり、外積代数の（ベクトル空間としての）双対空間にも乗法が定義され、その双対的な乗法が楔積と両立する。この双対代数は特に テンプレート:Mvar 上の重線型形式全体の成す多元環で、外積代数とその双対代数との双対性は内積によって与えられる。

動機付けとなる例

平面における面積

平行四辺形の面積は2つの頂点の座標を成分とする行列の行列式で表される。

平面 テンプレート:Math はベクトル空間であり、

${𝒆}_1=(1,0),{𝒆}_2=(0,1)$

という 2 つの単位ベクトルの組はその基底となっている。ここで、

$𝒗=v_1{𝒆}_1+v_2{𝒆}_2,𝒘=w_1{𝒆}_1+w_2{𝒆}_2$

という 2 つの成分表示された テンプレート:Math のベクトルが与えられたとすると、テンプレート:Math を 2 つの辺とする平行四辺形が一意に存在する。この平行四辺形の面積は、行列式を用いて

$A=|\det \left(\begin{array}{cc}𝒗& 𝒘\end{array}\right)|=|v_1{w}_2-v_2{w}_1|$

と表される。いま、テンプレート:Math の外積を

$\begin{array}{c}\\ 𝒗\wedge 𝒘& =(v_1{𝒆}_1+v_2{𝒆}_2)\wedge (w_1{𝒆}_1+w_2{𝒆}_2)\\ & =v_1{w}_1({𝒆}_1\wedge {𝒆}_1)+v_1{w}_2({𝒆}_1\wedge {𝒆}_2)+v_2{w}_1({𝒆}_2\wedge {𝒆}_1)+v_2{w}_2({𝒆}_2\wedge {𝒆}_2)\\ & =(v_1{w}_2-v_2{w}_1)({𝒆}_1\wedge {𝒆}_2)\end{array}$

のように定める。まず最初の部分では楔積に分配法則を適用し、ついで楔積が交代的であるという性質を用いた。最終的に得られた表式の係数はまさに行列 テンプレート:Math の行列式である。この係数が正負の値を取りうることは、直感的には、テンプレート:Math に、それらの定義する平行四辺形の辺として時計回りあるいは反時計回りの向きがつけられることを意味する。このような面積のことを平行四辺形の「符号つき面積」という。符号つき面積の絶対値は通常の意味での面積であり、符号はその向きを与えている。

この係数が符号つき面積となったことは偶然ではない。符号つき面積を代数的構造として公理化しようとすれば、必然的に外積と結びつくことが比較的簡単に確かめられる。詳しく言えば、テンプレート:Mvar と テンプレート:Mvar によって決まる平行四辺形の符号つき面積を テンプレート:Math と表すことにすれば、テンプレート:Mvar は下に挙げる性質を満たさなくてはならない。

1. 任意の実数 テンプレート:Mvar と テンプレート:Mvar について、テンプレート:Mvar が成り立つ。なぜならば、どちらかの辺の長さを変えれば、それに応じて面積も変わる。また、どちらかの辺の向きを変えれば、平行四辺形の向きは変わる。
2. テンプレート:Math である。なぜならば、テンプレート:Mvar が決める退化した平行四辺形（すなわち、線分）の面積は テンプレート:Math である。
3. テンプレート:Math である。なぜならば、テンプレート:Mvar と テンプレート:Mvar の役割を交換すれば平行四辺形の向きは逆転する。
4. テンプレート:Math である。なぜならば、テンプレート:Mvar の定数倍を テンプレート:Mvar に足すという作用は底辺の長さも高さも変えず、したがって面積を保つ。
5. テンプレート:Math である。なぜならば、単位正方形の面積は テンプレート:Math である。

最後の条件を除くと、楔積はこの面積の性質と同様の性質を満たす。ある意味で、楔積は面積の最後の性質を一般化し、適当に選んだ「標準的な」平行四辺形と比較することを許容したものであるといえる。言い換えれば、2 次元の外積は面積の「基底に依存しない」定式化である。

クロス積と三重積

テンプレート:Math におけるベクトルに対して、対応する外積代数はベクトルのクロス積およびスカラー三重積と近しい関係にある。標準基底 テンプレート:Math を用いて、2 つのベクトル

$𝒖=u_1{𝒆}_1+u_2{𝒆}_2+u_3{𝒆}_3,𝒗=v_1{𝒆}_1+v_2{𝒆}_2+v_3{𝒆}_3$

の楔積は 3-次元空間 テンプレート:Math の基底 テンプレート:Math に関して

$\begin{array}{cc}& 𝒖\wedge 𝒗\\ & =(u_1{v}_2-u_2{v}_1)({𝒆}_1\wedge {𝒆}_2)+(u_1{v}_3-u_3{v}_1)({𝒆}_1\wedge {𝒆}_3)+(u_2{v}_3-u_3{v}_2)({𝒆}_2\wedge {𝒆}_3)\end{array}$

と書くことができる。これは 3-次元における空間ベクトルの通常のクロス積の定義とよく似ている（通常のクロス積に落とすには後述のホッジの テンプレート:Math を用いればよい）。さらに 3 つ目のベクトルを

$𝒘=w_1{𝒆}_1+w_2{𝒆}_2+w_3{𝒆}_3$

とすれば、1-次元ベクトル空間 テンプレート:Math の基底 テンプレート:Math に関して、これら 3 つのベクトルの楔積は

$\begin{array}{cc}& 𝒖\wedge 𝒗\wedge 𝒘\\ & =(u_1{v}_2{w}_3+u_2{v}_3{w}_1+u_3{v}_1{w}_2-u_1{v}_3{w}_2-u_2{v}_1{w}_3-u_3{v}_2{w}_1)({𝒆}_1\wedge {𝒆}_2\wedge {𝒆}_3)\end{array}$

となる。これはスカラー三重積の通常の定義とよく似ている。

3-次元における通常のクロス積やスカラー三重積は幾何学的・代数的の両面で解釈することができる。クロス積 テンプレート:Math は テンプレート:Math と テンプレート:Math の両方に直交し、大きさがそれらの張る平行四辺形の面積の大きさに等しいようなベクトルとして解釈することができ、これはまた テンプレート:Math と テンプレート:Math を列ベクトルとする行列の小行列式を成分に持つベクトルとして解釈することもできる。 テンプレート:Math のスカラー三重積は幾何学的には（符号付）体積を表し、代数的には テンプレート:Math を列ベクトルとする行列の行列式となっている。3-次元における外積についても同様の解釈が許される。事実として、正の向きを持つ正規直交基底の存在性に関して、外積はこれらの概念をより高い次元へと一般化する。

形式的定義と代数的な性質

ベクトル空間 テンプレート:Mvar 上の外積代数 テンプレート:Math はテンソル代数 テンプレート:Math を テンプレート:Math の形の元で生成される両側イデアル テンプレート:Mvar で割ったテンプレート:仮リンクとして定義される。これを記号的に

$\bigwedge (V):=T(V)/I$

と表せば、テンプレート:Math の 2 元の楔積 テンプレート:Math は

$\alpha \wedge \beta =\alpha \otimes \beta (\mathrm{mod}I)$

で与えられる。

楔積の交代性

この積は テンプレート:Mvar の元の上で反対称的である。テンプレート:Math とすれば テンプレート:Math ゆえ

$0=(x+y)\wedge (x+y)=x\wedge x+x\wedge y+y\wedge x+y\wedge y=x\wedge y+y\wedge x$

が成り立つから

$x\wedge y=-y\wedge x$

が得られる。あるいはもっと一般に テンプレート:Math を テンプレート:Mvar の元、テンプレート:Mvar を整数 テンプレート:Math の置換 とすれば

$x_{\sigma (1)}\wedge x_{\sigma (2)}\wedge \cdots \wedge x_{\sigma (k)}=\mathrm{s}\mathrm{g}\mathrm{n}(\sigma )x_1\wedge x_2\wedge \cdots \wedge x_k$

が成立する。ここで テンプレート:Math は[[置換の符号|置換 テンプレート:Mvar の符号]]である。

外冪

テンプレート:Mvar の テンプレート:Mvar –次外冪 (テンプレート:En) テンプレート:Math とは

$x_1\wedge x_2\wedge \cdots \wedge x_k,x_i\in V,i=1,2,\dots ,k$

で張られる テンプレート:Math の部分線型空間である。

テンプレート:Math とするとき、テンプレート:Mvar は テンプレート:Mvar-重ベクトル (テンプレート:En) と呼ばれる。更に、テンプレート:Mvar が テンプレート:Mvar の テンプレート:Mvar 個の元の楔積で表すことができるならば、テンプレート:Mvar は分解可能 テンプレート:En であるという。

テンプレート:Math は分解可能多重ベクトルによって張られるけれども、全ての元が分解可能というわけではない。例えば、 テンプレート:Math で次の 2 重ベクトル

$\alpha =e_1\wedge e_2+e_3\wedge e_4$

は分解可能ではない（テンプレート:Math であり、実際にはこれは斜交形式である）。

基底と次元

テンプレート:Mvar の次元を有限な テンプレート:Mvar とし、テンプレート:Math を テンプレート:Mvar の一つの基底とする。このとき、集合

$\{e_{i_1}\wedge e_{i_2}\wedge \cdots \wedge e_{i_k}\mid 1\le i_1<i_2<\cdots <i_k\le n\}$

は テンプレート:Mvar-次外冪 テンプレート:Math の基底を成す。実際に任意の元が

$v_1\wedge \cdots \wedge v_k$

の形に与えられたとき、各ベクトル テンプレート:Mvar は基底 テンプレート:Mvar の線型結合に書けるから、楔積の重線型性を使って展開すればこれを基底ベクトル同士の楔積の線型結合に書き直すことができる。このとき、楔積の中に同じベクトルがあれば テンプレート:Math になるし、基底ベクトルが順番に現われていなければ符号を変えて順番を入れ替えて、基底を順番通りに並ばせることができる。 一般に、結果として得られた テンプレート:Mvar-ベクトルの基底の係数は基底 テンプレート:Mvar に関してベクトル テンプレート:Mvar を記述する行列の小行列式として計算できる。

基底に属する元の個数を数えることにより テンプレート:Math の次元は二項係数 テンプレート:Math で与えられることが分かる。特に、テンプレート:Math ならば テンプレート:Math である。

外積代数の任意の元は多重ベクトルの和として表される。よって、外積代数はベクトル空間の直和

$\bigwedge (V)={\bigwedge }^0(V)\oplus {\bigwedge }^1(V)\oplus {\bigwedge }^2(V)\oplus \cdots \oplus {\bigwedge }^n(V)$

に分解される（ここで テンプレート:Math および テンプレート:Math と約束する）。したがって外積代数の次元は二項係数の和に等しく、テンプレート:Math である。

多重ベクトルの階数

テンプレート:Math とすると テンプレート:Mvar は分解可能多重ベクトルの線型結合

$\alpha ={\alpha }^{(1)}+{\alpha }^{(2)}+\cdots +{\alpha }^{(s)}$

として表示できる。ここで各 テンプレート:Math は分解可能、つまり

${\alpha }^{(i)}={\alpha }_1^{(i)}\wedge \cdots \wedge {\alpha }_k^{(i)},i=1,2,\dots ,s$

と書ける。多重ベクトル テンプレート:Mvar の階数 テンプレート:Enとは テンプレート:Mvar のこのような表示に現れる分解可能多重ベクトルの最小数をいう。これはテンプレート:仮リンクの記法の類似である。

階数は特に 2 重ベクトルの研究で重要であるテンプレート:Harv テンプレート:Harv。2-重ベクトル テンプレート:Mvar の階数は テンプレート:Mvar のある基底に関する係数の作る行列の階数と同一視できる。つまり、テンプレート:Math を テンプレート:Mvar の基底とすると、テンプレート:Mvar は

$\alpha =\sum _{i,j}{a}_{ij}{e}_i\wedge e_j$

と一意的に表示できる（ここで テンプレート:Math ゆえ、対応する係数行列は歪対称行列である）。そして テンプレート:Mvar の階数は行列 テンプレート:Math の階数に一致する。

標数 テンプレート:Math の場合、2-重ベクトル テンプレート:Mvar が階数 テンプレート:Mvar を持つことと

$\underset{p}{\underbrace{\alpha \wedge \cdots \wedge \alpha }}=0$

かつ

$\underset{p+1}{\underbrace{\alpha \wedge \cdots \wedge \alpha }}=0$

であることとは同値である。

次数付け構造

テンプレート:Mvar-重ベクトルと テンプレート:Mvar-重ベクトルとの楔積は テンプレート:Math-重ベクトルで、双線型性を持つことを思い出そう。結果として先行節で与えた直和分解

$\bigwedge (V)={\bigwedge }^0(V)\oplus {\bigwedge }^1(V)\oplus {\bigwedge }^2(V)\oplus \cdots \oplus {\bigwedge }^n(V)$

は外積代数に次数付き代数の構造を与える。記号的には

$({\bigwedge }^k(V))\wedge ({\bigwedge }^p(V))\subset {\bigwedge }^{k+p}(V)$

が成り立つ。さらに楔積は次数付き反対称性を持つ。つまり テンプレート:Math と テンプレート:Math に対し

$\alpha \wedge \beta =(-1{)}^{kp}\beta \wedge \alpha$

が成立する。外積代数の次数付き構造の研究に加えてテンプレート:Harvtxtは、（それ自身次数付けを持つ加群である）次数付き加群上の外積代数のような、外積代数上の加法的次数付き構造を研究した。

普遍性

テンプレート:Mvar を体 テンプレート:Mvar 上のベクトル空間とする。形式張らずに言えば、テンプレート:Math における乗法は文字を分配法則、結合法則と恒等式 テンプレート:Math に従って操作することによって行われる。厳密には テンプレート:Math は乗法がそれらの法則を満足する多元環の中で、「もっとも一般」なものである。それは テンプレート:Mvar を含み交代的な乗法を持つ任意の単位的結合 テンプレート:Mvar-代数は テンプレート:Math の準同型像として得られるという意味である。言い換えれば、外積代数は以下の普遍性を持つ。

外積代数の普遍性

与えられた任意の単位的結合 テンプレート:Mvar-代数 テンプレート:Mvar と任意の テンプレート:Mvar-線型写像 テンプレート:Math で テンプレート:Math を満たすものに対して、 単位的テンプレート:仮リンク テンプレート:Math で テンプレート:Math を満たすものが「唯一つ」存在する。

外積代数の普遍性

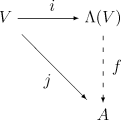
テンプレート:Mvar を含み、テンプレート:Mvar の上で交代的な乗法を持つもっとも一般の多元環を構成するには、テンプレート:Mvar を含む最も一般な多元環であるテンソル代数 テンプレート:Math から始めるのが自然であり、テンソル代数の適当な商をとることによって交代性を導入してやればよい。そこで テンプレート:Math の形の元全体が生成する テンプレート:Math の両側イデアル テンプレート:Mvar をとり、テンプレート:Math を

$\bigwedge (V)=T(V)/I$

で定義して、テンプレート:Math における乗法を表す記号として テンプレート:Math (テンプレート:En) を用いる。この テンプレート:Math が テンプレート:Mvar を含み、上記の普遍性を満たすことはすぐに判る。

この構成の結果として、ベクトル空間 テンプレート:Mvar に外積代数 テンプレート:Math に対応させる操作が、ベクトル空間の圏から多元環の圏への函手となる。

空間 テンプレート:Math を始めに定義して、それらの直和として代数 テンプレート:Math を構成する代わりに、最初に テンプレート:Math を定義して、外冪 テンプレート:Math を適当な部分空間と同一視するほうを好むかもしれない。このやり方はしばしば微分幾何で用いられる（次の節で記述する）。

一般化

与えられた可換環 テンプレート:Mvar と [[環上の加群|テンプレート:Mvar-加群]] テンプレート:Mvar に対して、上でやったようにテンソル代数 テンプレート:Math の適当な商として外積代数 テンプレート:Math を定義することができる。それは類似の普遍性を満足するだろう。テンプレート:Math の多くの性質は テンプレート:Mvar が射影加群であることを要求する。有限次元性が用いられるところでは、テンプレート:Mvar を有限生成かつ射影的とすることが必要である。もっと一般の設定への一般化は テンプレート:Harv に見つかる。

位相幾何学などでベクトル束の外積代数を考えることがしばしばある。セール–スワンの定理により、有限次元ベクトル束の外積代数の代数的性質と有限生成射影加群の外積代数のそれとの間には本質的な違いはない。もっと一般に外積代数は加群の層に対して定義できる。

双対性

交代作用素

2 つのベクトル空間 テンプレート:Mvar に対し、テンプレート:Mvar から テンプレート:Mvar への交代作用素 (テンプレート:En) あるいは反対称作用素 (テンプレート:En) とは多重線型写像

テンプレート:Math

であって、テンプレート:Math が線型従属なベクトルならば

テンプレート:Math

を常に満たすもののことである。最も有名な例は行列式でこれは テンプレート:Math から テンプレート:Mvar への交代作用素である。また、テンプレート:Mvar の テンプレート:Mvar 個のベクトルにその楔積となる テンプレート:Mvar-重ベクトルを対応させる写像

テンプレート:Math

も交代的である。事実として、この写像は テンプレート:Mvar 上定義される交代作用素の中で「もっとも一般」なものである。つまり、交代作用素 テンプレート:Math が与えられたとき、線型写像 テンプレート:Math で テンプレート:Math を満たすものが唯一つ存在する。この普遍性により テンプレート:Math を特徴づけられる。この普遍性を テンプレート:Math の定義とすることもある。

重線型交代形式

上記の特別の場合として テンプレート:Math を基礎体とするとき、交代重線型写像

テンプレート:Math

は重線型交代形式と呼ばれる。重線型交代形式の全体の成す集合は、それらの和もスカラー倍も再び交代性を持つから、ベクトル空間を成す。 外冪の普遍性により、テンプレート:Mvar 上の次数 テンプレート:Mvar の交代形式の空間は双対空間 テンプレート:Math と自然同型である。テンプレート:Mvar が有限次元なら後者は テンプレート:Math に自然同型である。特に テンプレート:Mvar から テンプレート:Mvar への反対称写像全体の成す空間の次元は テンプレート:Mvar から テンプレート:Mvar を選ぶ二項係数に等しい。

この同一視の元、楔積は具体的な形で 2 つの反対称写像から別の反対称写像を導く。テンプレート:Math と テンプレート:Math を 2 つの反対称写像とする。重線型写像のテンソル積の場合と同様に楔積における変数の個数はそれぞれの写像の変数の個数の和になる。楔積は次のように

$\omega \wedge \eta =\frac{(k+m)!}{k!m!}\mathrm{Alt}(\omega \otimes \eta )$

と定義される。ここで重線型写像の交代化作用 "テンプレート:Math" は変数の置換全体を亘る符号付平均

$\mathrm{Alt}(\omega )(x_1,\dots ,x_k)=\frac{1}{k!}\sum _{\sigma \in S_k}\mathrm{sgn}(\sigma )\omega (x_{\sigma (1)},\dots ,x_{\sigma (k)})$

で定義される。この楔積の定義は、テンプレート:Mvar が有限標数をもてば矛盾無く定まる。上記と同値で階乗を使わないものとして

$\begin{array}{cc}& (\omega \wedge \eta )(x_1,\dots ,x_{k+m})\\ & =\sum _{\sigma \in {\mathrm{Sh}}_{k,m}}\mathrm{sgn}(\sigma )\omega (x_{\sigma (1)},\dots ,x_{\sigma (k)})\eta (x_{\sigma (k+1)},\dots ,x_{\sigma (k+m)})\end{array}$

を考えることもできる。ここで テンプレート:Math は テンプレート:Math-テンプレート:仮リンク全体の成す部分集合である。テンプレート:Math-シャッフルは テンプレート:Math の置換 テンプレート:Mvar であって、テンプレート:Math かつ テンプレート:Math なるものを言う。

双代数構造

正確に言えば、次数付き代数 テンプレート:Math の次数付き双対と テンプレート:Mvar 上の重線型交代形式全体の空間の間に対応が存在する。上で定義した重線型代数の楔積は テンプレート:Math 上に定義され、余代数の構造を定める余積の双対である。

この余積 (テンプレート:En) は線型写像 テンプレート:Math であって、分解可能な元の上では

$\mathrm{\Delta }(x_1\wedge \cdots \wedge x_k)=\sum _{p=0}^k\sum _{\sigma \in {\mathrm{Sh}}_{p,k-p}}\mathrm{sgn}(\sigma )(x_{\sigma (1)}\wedge \cdots \wedge x_{\sigma (p)})\otimes (x_{\sigma (p+1)}\wedge \cdots \wedge x_{\sigma (k)})$

によって与えられる。例えば

$\mathrm{\Delta }(x_1)=1\otimes x_1+x_1\otimes 1,$

$\mathrm{\Delta }(x_1\wedge x_2)=1\otimes (x_1\wedge x_2)+x_1\otimes x_2-x_2\otimes x_1+(x_1\wedge x_2)\otimes 1$

のようである。これを線型に拡張して外積代数全体で定義される演算を得る。余積の言葉で言えば、双対空間上の楔積はちょうど余積の次数つき双対

$(\alpha \wedge \beta )(x_1\wedge \cdots \wedge x_k)=(\alpha \otimes \beta )(\mathrm{\Delta }(x_1\wedge \cdots \wedge x_k))$

である。ここで右辺におけるテンソル積は線型写像としてのそれである（両立しない斉次次数の元については テンプレート:Math で拡張する。もっとはっきり言えば テンプレート:Math と定める。ここで テンプレート:Mvar は以下で定義する余単位射である）。

余単位射 テンプレート:En は準同型 テンプレート:Math で引数の テンプレート:Math-次成分を返すものである。余積および余単位射は楔積とともに外積代数に双代数の構造を定める。

内部積

テンプレート:See also テンプレート:Mvar は有限次元とし、テンプレート:Math を テンプレート:Mvar の双対空間とする。任意の テンプレート:Math に対し、代数 テンプレート:Math 上のテンプレート:仮リンク

$i_{\alpha }:{\bigwedge }^k(V)\to {\bigwedge }^{k-1}(V)$

が定義できる。この微分を テンプレート:Mvar に関する内積あるいは内部積 (テンプレート:En) と呼ぶ。挿入作用素 (テンプレート:En) や テンプレート:Mvar による縮約 (テンプレート:En) などということもある。

テンプレート:Math とすると、テンプレート:Math は テンプレート:Math から テンプレート:Math への重線型写像であるから、テンプレート:Mvar-重直積 テンプレート:Math における値によって定まる。テンプレート:Math の テンプレート:Math 個の元 テンプレート:Math に対し、

$(i_{\alpha }𝐰)(u_1,u_2,\dots ,u_{k-1})=𝐰(\alpha ,u_1,u_2,\dots ,u_{k-1})$

が定義される。加えて、テンプレート:Mvar が純スカラー（つまり、テンプレート:Math の元）であるときには テンプレート:Math とする。

公理的特徴づけと性質

内部積は以下の性質

1. 任意の テンプレート:Mvar と任意の テンプレート:Math について$$i_{\alpha }:{\bigwedge }^k(V)\to {\bigwedge }^{k-1}(V)$$である（規約により テンプレート:Math とする）。
2. テンプレート:Mvar が テンプレート:Math の元ならば テンプレート:Math とする。
3. 任意の テンプレート:Math に対し、テンプレート:Mvar は次数 テンプレート:Math のテンプレート:仮リンク$$i_{\alpha }(a\wedge b)=(i_{\alpha }a)\wedge b+(-1{)}^{\mathrm{deg}a}a\wedge (i_{\alpha }b)$$である。

を満足する。事実として、これら 3 つの性質は、内部積を特徴付けるのに十分で、一般の無限次元の場合においても内部積を同様に定義する。内部積のほかの性質としては

• $i_{\alpha }\circ i_{\alpha }=0,$
• $i_{\alpha }\circ i_{\beta }=-i_{\beta }\circ i_{\alpha }$

が挙げられる。

ホッジ双対性

テンプレート:Main テンプレート:Mvar を有限 テンプレート:Mvar-次元とすると、内部積はベクトル空間の自然な同型

${\bigwedge }^k(V^{*})\otimes {\bigwedge }^n(V)\to {\bigwedge }^{n-k}(V)$

を誘導する。幾何学的な設定で、（一次元ベクトル空間である）最高次外冪 テンプレート:Math のゼロでない元はしばしば体積要素と（あるいは多少紛らわしい用語だが テンプレート:En とも）呼ばれる。体積要素 テンプレート:Mvar に関して上記の同型は

$\alpha \in {\bigwedge }^k(V^{*})\mapsto i_{\alpha }\sigma \in {\bigwedge }^{n-k}(V)$

によって明示的に与えられる。体積要素に加えて、ベクトル空間 テンプレート:Mvar が テンプレート:Mvar と テンプレート:Math を同一視する内積を備えているならば、得られる同型

$*:{\bigwedge }^k(V)\to {\bigwedge }^{n-k}(V)$

はホッジ双対、あるいは一般には[[ホッジ作用素|ホッジ テンプレート:Math-作用素]]と呼ばれる。テンプレート:Math-作用素とそれ自身の合成写像 テンプレート:Math は常に恒等写像のスカラー倍である。ほとんどの応用においては、体積形式はそれが テンプレート:Mvar のある正規直交基底の楔積であるという意味で内積と両立する。この場合は

$*\circ *:{\bigwedge }^k(V)\to {\bigwedge }^k(V)=(-1{)}^{k(n-k)+q}I$

になっている。ここで テンプレート:Mvar は恒等写像で、内積は計量符号数 テンプレート:Math （プラスが テンプレート:Mvar 個、マイナスが テンプレート:Mvar 個）を持つ。

函手性

テンプレート:Mvar をベクトル空間の対とし、テンプレート:Math を線型写像とする。このとき普遍構成により、次数付き代数の準同型

$\bigwedge (f):\bigwedge (V)\to \bigwedge (W)$

であって、その テンプレート:Math への制限が

$\bigwedge (f){|}_V=f$

を満たすようなものが唯一つ存在する。特に テンプレート:Math は斉次次数 (テンプレート:En) を保つ。テンプレート:Math の テンプレート:Mvar-次成分は分解可能元の上では

$\bigwedge (f)(x_1\wedge \cdots \wedge x_k)=f(x_1)\wedge \cdots \wedge f(x_k)$

で与えられる。

${\bigwedge }^k(f)=\bigwedge (f{)}_{{\bigwedge }^k(V)}:{\bigwedge }^k(V)\to {\bigwedge }^k(W)$

とすると、変換 テンプレート:Math の テンプレート:Mvar と テンプレート:Mvar の基底に関する成分は テンプレート:Mvar の テンプレート:Math 小行列式の作る行列である。特に、テンプレート:Math で テンプレート:Mvar が有限 テンプレート:Mvar-次元のとき、テンプレート:Math は 1 次元ベクトル空間 テンプレート:Math をそれ自身に移すから、これはスカラーで与えられ、それはちょうど テンプレート:Mvar の行列式の値である。

完全性

ベクトル空間の短完全列

$0\to U\to V\to W\to 0$

に対し、

$0\to {\bigwedge }^1(U)\wedge \bigwedge (V)\to \bigwedge (V)\to \bigwedge (W)\to 0$

は次数付き線型空間の完全列である。もちろん

$0\to \bigwedge (U)\to \bigwedge (V)$

も完全である。

直和

ベクトル空間の直和上の外積代数はそれぞれの空間上の外積代数のテンソル積に同型

$\bigwedge (V\oplus W)=\bigwedge (V)\otimes \bigwedge (W)$

である。これは次数付き同型、つまり

${\bigwedge }^k(V\oplus W)=\underset{p+q=k}{⨁}{\bigwedge }^p(V)\otimes {\bigwedge }^q(W)$

になっている。もう少し一般に

$0\to U\to V\to W\to 0$

がベクトル空間の短完全列ならば テンプレート:Math はテンプレート:仮リンク

$0=F^0\subseteq F^1\subseteq \cdots \subseteq F^k\subseteq F^{k+1}={\bigwedge }^k(V)$

で、その商が

$F^{p+1}/F^p={\bigwedge }^{k-p}(U)\otimes {\bigwedge }^p(W)$

なるものを持つ。特に、テンプレート:Mvar が 1 次元ならば

$0\to U\otimes {\bigwedge }^{k-1}(W)\to {\bigwedge }^k(V)\to {\bigwedge }^k(W)\to 0$

は完全であり、テンプレート:Mvar が 1 次元ならば

$0\to {\bigwedge }^k(U)\to {\bigwedge }^k(V)\to {\bigwedge }^{k-1}(U)\otimes W\to 0$

が完全である。

交代テンソル代数

テンプレート:Mvar を標数 テンプレート:Math の体とするとき、ベクトル空間 テンプレート:Mvar の外積代数はテンソル空間 テンプレート:Math の交代テンソル全体の成す部分空間と自然に同一視される。外積代数が テンプレート:Math の テンプレート:Math で生成されるイデアルによる商多元環として定義されたことを思い出そう。

テンプレート:Math を次数 テンプレート:Mvar の斉次テンソル全体の成すベクトル空間とすれば、テンプレート:Math は分解可能テンソル

$v_1\otimes \cdots \otimes v_r,(v_i\in V)$

で生成される。分解可能テンソルの交代化作用素 (テンプレート:En) あるいは歪対称化作用素 (テンプレート:En) は

$\mathrm{Alt}(v_1\otimes \cdots \otimes v_r)=\frac{1}{r!}\sum _{\sigma \in {𝔖}_r}\mathrm{sgn}(\sigma )v_{\sigma (1)}\otimes \cdots \otimes v_{\sigma (r)}$

で与えられる。ここに和は文字 テンプレート:Math の置換全体の成す対称群を亘る。これを線型性と斉次性を使ってテンソル空間 テンプレート:Math 全体まで拡張したものも同じく "テンプレート:Math" で表す。テンプレート:Math の像 テンプレート:Math を交代テンソル代数 (テンプレート:En) と呼び、テンプレート:Math で表す。これは テンプレート:Math の部分線型空間で、テンプレート:Math から次数付きベクトル空間の構造が遺伝する。これにより結合的な次数付き乗法が

$t\hat{\mathrm{\otimes }}s=\mathrm{Alt}(t\otimes s)$

によって誘導される。しかしこれはテンソル積とは異なる乗法であって、テンプレート:Math の核がちょうど両側イデアル テンプレート:Mvar に一致して（テンプレート:Mvar は標数 テンプレート:Math だと仮定している）、自然な同型

$A(V)\cong \bigwedge (V)$

が存在する。

指数表記

テンプレート:Mvar が有限 テンプレート:Mvar-次元であるとし、その基底 テンプレート:Math が与えられているとする。交代テンソル テンプレート:Math は添字表記を用いて

$t=t^{i_1{i}_2\dots i_r}{𝒆}_{i_1}\otimes {𝒆}_{i_2}\otimes \cdots \otimes {𝒆}_{i_r}$

と書ける。ここで テンプレート:Math はその添字に関して完全反対称である。

階数がそれぞれ テンプレート:Mvar および テンプレート:Mvar である交代テンソル テンプレート:Mvar および テンプレート:Mvar の楔積は

$t\hat{\mathrm{\otimes }}s=\frac{1}{(r+p)!}\sum _{\sigma \in {𝔖}_{r+p}}\mathrm{sgn}(\sigma )t^{i_{\sigma (1)}\dots i_{\sigma (r)}}{s}^{i_{\sigma (r+1)}\dots i_{\sigma (r+p)}}{𝒆}_{i_1}\otimes {𝒆}_{i_2}\otimes \cdots \otimes {𝒆}_{i_{r+p}}$

で与えられる。このテンソルの成分はちょうどテンソル積 テンプレート:Math の成分の交代部分になっており、添字に角括弧をつけて

$(t\hat{\mathrm{\otimes }}s{)}^{i_1\dots i_{r+p}}=t^{[i_1\dots i_r}{s}^{i_{r+1}\dots i_{r+p}]}$

と表す。

内部積も添字記法で書くことができる。

$t=t^{i_0{i}_1\dots i_{r-1}}$

を階数 テンプレート:Mvar の反対称テンソルとすると、テンプレート:Math に対して テンプレート:Math は階数 テンプレート:Math の交代テンソルで

$(i_{\alpha }t{)}^{i_1\dots i_{r-1}}=r\sum _{j=0}^n{\alpha }_j{t}^{j{i}_1\dots i_{r-1}}$

によって与えられる。テンプレート:Mvar は テンプレート:Mvar の次元である。

応用

線型代数

分解可能 テンプレート:Mvar-ベクトルは幾何学的に解釈することができる。2-ベクトル テンプレート:Math は テンプレート:Mvar で張られる、テンプレート:Mvar と テンプレート:Mvar を辺に持つ向き付けられた平行四辺形の面積で与えられる数の「重み」を持つ平面を表す。同様にして 3-ベクトル テンプレート:Math は、テンプレート:Mvar を辺とする平行六面体の体積で重み付けられた 3 次元空間を表す。

射影幾何

テンプレート:Math の分解可能 テンプレート:Mvar-ベクトルは テンプレート:Mvar の重み付き テンプレート:Mvar-次元部分空間に対応する。特に テンプレート:Mvar の テンプレート:Mvar-次元部分空間のグラスマン多様体 テンプレート:Math は自然に射影空間 テンプレート:Math のある代数多様体と同一視される。これをテンプレート:仮リンクという。

微分幾何

外積代数の微分幾何における特筆すべき応用は、微分形式の定義に用いられることである。可微分多様体上の点における微分形式は、その点の接空間における重線型交代形式であり、テンプレート:Mvar-次微分形式は接空間の テンプレート:Mvar-次外冪からの線型汎函数である。結論として、重線型形式の楔積は自然に微分形式の楔積を定める。微分形式は微分幾何のさまざまな部分で大きな役割を担う。

特に、外微分は多様体上の微分形式に外積代数に微分環の構造を与える。外微分は多様体間の滑らかな写像に沿っての引き戻しと可換であり、それゆえに自然な微分作用素である。外微分を備えた微分形式の外積代数は、そのコホモロジーが台となる多様体のド・ラームコホモロジーと呼ばれる微分複体を成し、可微分多様体の代数的位相幾何学の根幹を成している。

表現論

表現論において、外積代数はベクトル空間の圏における二つの基本テンプレート:仮リンクのうちの一つで、もう一方は対称代数である。これらの構成はともに一般線型群の既約表現を生み出すのに用いられる。

物理学

外積代数は、フェルミオンと超対称性に関する物理理論において基本的な役割を演じる、テンプレート:仮リンクの原型的な例である。物理学的な議論はグラスマン数を見よ。ほかのいくつかの関連する概念の物理学への応用はテンプレート:仮リンクやテンプレート:仮リンクを参照。

歴史

外積代数は1844年、『拡大の理論』(テンプレート:De) の包括的な言葉の下にヘルマン・グラスマンによって初めて導入された。これはもっと一般に量の拡大の代数的（あるいは公理的）な理論について言及しており、また早い時期における現代的なベクトル空間の概念のさきがけの一つとなっている。テンプレート:仮リンクもまた同様の テンプレート:En の概念を著しており、それがグラスマンに先駆けて成されたものと主張した。

外積代数それ自身は、アーサー・ケイリーとジェームス・ジョセフ・シルベスターの重ベクトルの理論の形式的側面を捉えたいくつかの規約あるいは公理から組み立てられたもので、それゆえに幾何学的な言葉での形式的な理由付けの面を抜きにすれば、命題計算のような「計算」(テンプレート:En) の類である。 特にこの新たな発展は、それまで座標の観点からのみ説明されてきた性質である次元の概念の「公理的な」特徴づけを可能にした。

このベクトルと重ベクトルに関する新しい理論の重要性は19世紀半ばまでには失われ、1888年にジュゼッペ・ペアノによって詳しく調べられるまで顧みられることは無かった。ペアノの仕事にも幾分不明瞭な部分が残されていたが、世紀が変わる頃には、微分形式の計算にグラスマンのアイデアを応用したフランス高等師範学校のメンバー（有名どころはアンリ・ポアンカレ、エリ・カルタン、ジャン・ガストン・ダルブーら）によって主題の統一をみた。

そのしばらく後にアルフレッド・ノース・ホワイトヘッドはペアノとグラスマンのアイデアをもとにして普遍代数を導入する。これは確固たる論理的基礎の上に代数系の公理的な概念を与えることで、20世紀の抽象代数学の発展を可能にした。

関連項目

• 対称代数 — 外積代数の（積が）対称な場合の類似物
• クリフォード代数 — 外積代数の二次形式による量子化
• ワイル代数 — 対称代数のシンプレクティック形式による量子化
• 多重線型代数学
• テンソル代数
• テンプレート:仮リンク
• テンプレート:仮リンク

参考文献

数学的内容に関して

• テンプレート:Citation
  • Includes a treatment of alternating tensors and alternating forms, as well as a detailed discussion of Hodge duality from the perspective adopted in this article.
• テンプレート:Citation
  • This is the main mathematical reference for the article. It introduces the exterior algebra of a module over a commutative ring (although this article specializes primarily to the case when the ring is a field), including a discussion of the universal property, functoriality, duality, and the bialgebra structure. See chapters III.7 and III.11.
• テンプレート:Citation
  • This book contains applications of exterior algebras to problems in partial differential equations. Rank and related concepts are developed in the early chapters.
• テンプレート:Citation
  • Chapter XVI sections 6-10 give a more elementary account of the exterior algebra, including duality, determinants and minors, and alternating forms.
• テンプレート:Citation
  • Contains a classical treatment of the exterior algebra as alternating tensors, and applications to differential geometry.

歴史的内容に関して

• テンプレート:Cite book
• テンプレート:Citation
• テンプレート:Citation
• テンプレート:Citation (The Linear Extension Theory - A new Branch of Mathematics)
• テンプレート:Citation
• テンプレート:Citation [Geometric Calculus according to Grassmann's Ausdehnungslehre, preceded by the Operations of Deductive Logic]
• テンプレート:Citation

その他の文献および関連図書

• テンプレート:Citation
  • An introduction to the exterior algebra, and geometric algebra, with a focus on applications. Also includes a history section and bibliography.
• テンプレート:Citation
  • Includes applications of the exterior algebra to differential forms, specifically focused on integration and Stokes's theorem. The notation Λ^kV in this text is used to mean the space of alternating k-forms on V; i.e., for Spivak Λ^kV is what this article would call Λ^kV*. Spivak discusses this in Addendum 4.
• テンプレート:Citation
  • Includes an elementary treatment of the axiomatization of determinants as signed areas, volumes, and higher-dimensional volumes.
• テンプレート:SpringerEOM
• Wendell H. Fleming (1965) Functions of Several Variables, Addison-Wesley.
  • Chapter 6: Exterior algebra and differential calculus, pages 205-38. This textbook in multivariate calculus introduces the exterior algebra of differential forms adroitly into the calculus sequence for colleges.
• 若木喬 (2011) "テンプレート:Wayback"
  • Grassmann, Hermannの書Ausdehnungslehreの忠実な解釈に基づき、現代的な記号化と表現で新しい数学体系として"グラスマンの外積代数"を確立し、理工学分野の多くの問題の解析に応用している。

テンプレート:Tensors テンプレート:Linear algebra